1. 注意力提示
1.1 生物学的注意力提示
如下的观察实验:
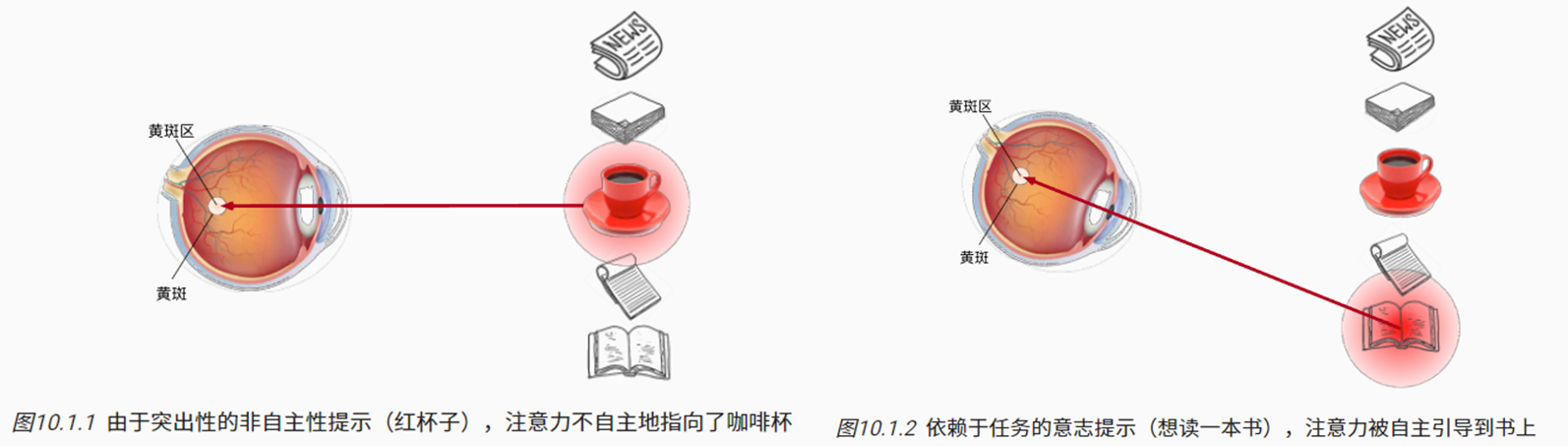
- 受试者的注意力往往首先被颜色鲜艳的红色咖啡杯吸引(非自主性);
- 客观存在的,对于观察者的吸引特征。
- 喝完咖啡,处于兴奋状态的大脑经思考后,相比看报等,可能更想要读一本书(自主性权重更高);
- 在受试者的主观意愿推动下所做的决定。
1.2 查询、键和值
- 上述的非自主性提示,可以类比之前的全连接层、卷积层等。
- 红色的咖啡杯可以理解为高权重值的神经元,对输出有较大的影响。
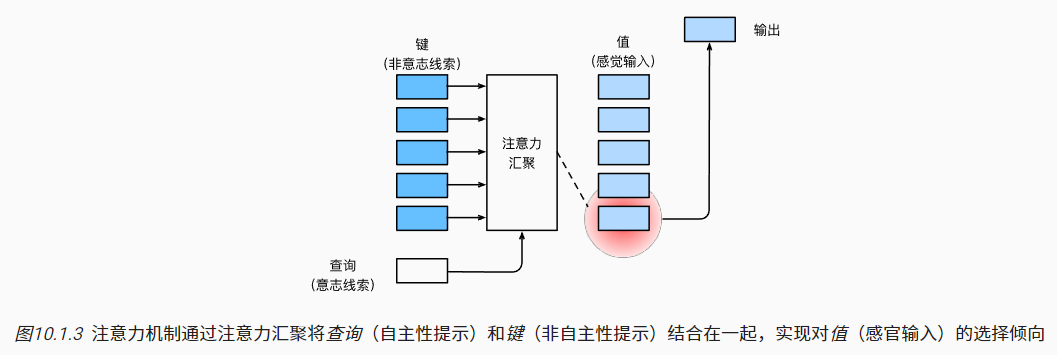
- 而注意力(Attention)机制可通过注意力汇聚,将查询(Query)与所有的键值(Key-Value)对进行关联,得到输出。
- 查询:分别与所有键Key计算’相似度’,表示权重值,得到注意力的抽象表示;
- 键-值对:基于上述权重,对值value进行加权平均求和,得到输出。(二者可以是同一数据)
- 一个Query得到一个输出
1.3 注意力的可视化
- 对注意力的权重进行热图可视化
- 每行表示一次Query与所有的Key计算的权重结果。
|
|
2. 注意力汇聚
- 1964年提出的Nadaraya-Watson核回归,本质上可以理解为带有加权平均的注意力机制
2.1 生成数据集
x_train:键Keyy_train:值Valuex_test:查询Query
|
|
2.2 平均汇聚
- 最简单的做法是对于任意Query(x),都直接计算所有训练样本输出值(yi)的均值
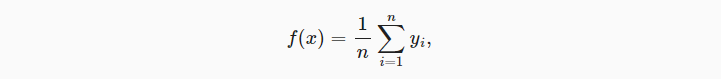
|
|
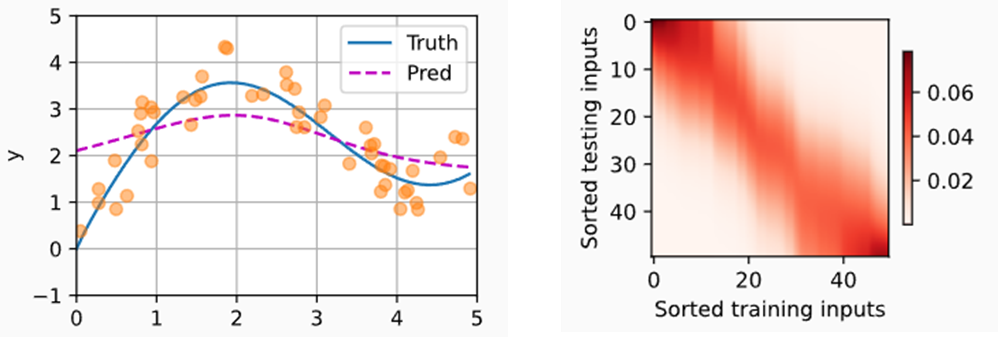
2.3 非参数注意力汇聚
- 根据query(x)与key(xi)的关系度量α,计算当key为xi时,值yi的权重。
- 一种关系度量方式是将x与xi间的距离进行高斯核函数转换。距离越近,则值越大。
- 最后的Softmax操作将权重和变为1,得到最终的加权平均方式。
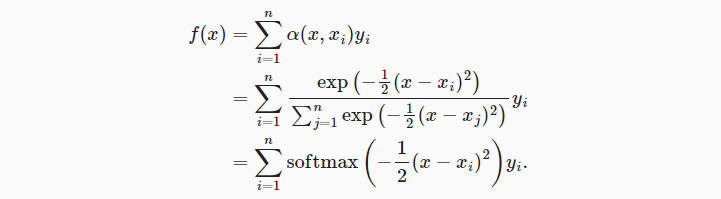
- 下述的计算为非参数的注意力汇聚,即没有可学习的模型参数。
|
|
|
|
2.4 带参数注意力汇聚
- 如下,是带可学习参数的Nadaraya-Watson核回归实现
- w参数用于控制高斯核的宽度,可以理解为方差。
- 方差越大,表示越关注少数几个与query高度接近的xi,赋予较高的权重。
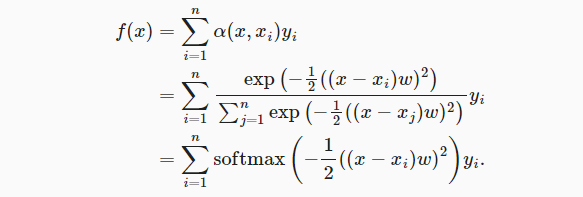
(1)批量矩阵乘法
nn.bmm: 第一个小批量的第i个矩阵与第二个小批量的第i个矩阵相乘。
|
|
- 据此,可在注意力机制背景下,计算小批量数据的加权平均值
|
|
(2)定义模型
- w可学习参数
|
|
(3)训练
- 计算keys与values
- 因为要使用x_train作为query,所以在keys与values中的每一行中,去除自己本身的观测键值对
|
|
- 训练
- 训练模型使用x_train作为query,而不是x_test;
- x_train中的第i个query与keys中的第i行进行α计算;
- 得到对应的权重结果后,再对values的第i行进行加权平均、
|
|
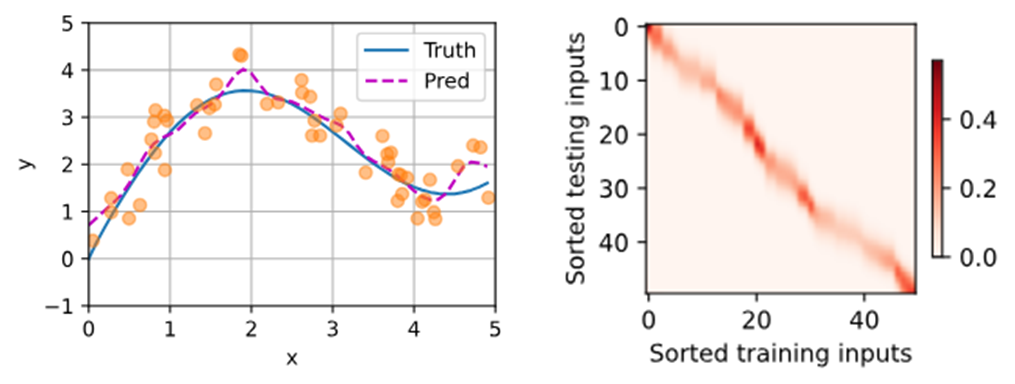
- 预测
|
|
|
|
如上右图,可以看到w参数将注意力机制更关注少数与query权重更高的key
3. 注意力评分函数
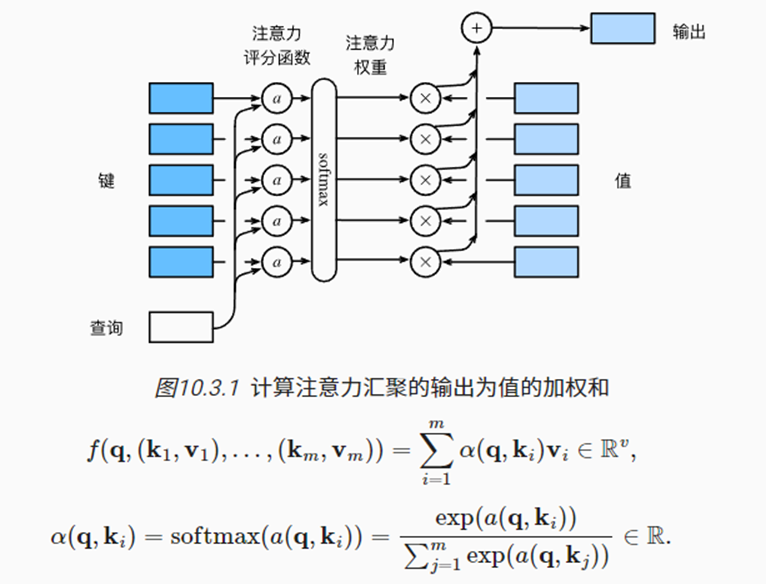
- 上面的α(高斯运算)可以视为注意力评分函数,计算query与每个key的’关系’。然后再经softmax操作,映射为注意力权重。
- 引申来看,如下公式中:
- q表示查询query,可以是一个向量;
- (k, v)表示键值对(key-value),二者可以是长度不同的向量,也可以是同一数据;
- 评分函数 α(q, ki)将query与每个key映射成标量,再进行softmax计算。
|
|
3.1 掩蔽softmax操作
- 在上一章的seq2seq学习中,为了保证子序列长度相同,对于原来较短的序列进行了填充。
- 同样,这里需要将这些填充词元的注意分数设置为很小的值,从而在softmax操作时计算得到权重值为0。
|
|
- 示例操作
|
|
3.2 加性注意力
- Activation attention:将查询向量与键的向量相加后,输入到一个多层感知机中
- 单隐藏层,tanh激活函数,禁用偏置项,输出层的神经元个数为1

|
|
- 示例操作:批量大小为2,每个批量
- 1个query,其向量长度为20
- 10对key-value,key向量长度为2,value向量长度为4
|
|
- 注意力汇聚输出的形状为(批量大小,查询数,值value的维度)
|
|
- 每个query对于所有key的注意力权重可视化
|
|
3.3 缩放点积注意力
- Scaled dot-product attention:当query向量与key向量长度一致时,可进行点积操作;再根据向量长度进行缩放,作为注意力分数。
- 相比于加性注意力,模型参数较少(只有dropout)
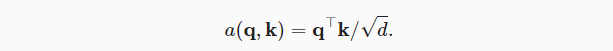
|
|
- 示例操作
|
|
4. Bahdanau注意力
- 在上一章学习seq2seq时,将编码器RNN中最后一个时间步的隐状态作为上下文变量传递给了解码器。
- 此时,假设该隐状态能够学习到编码器序列的全部信息,但对于较长的序列,实际情况可能并非如此。
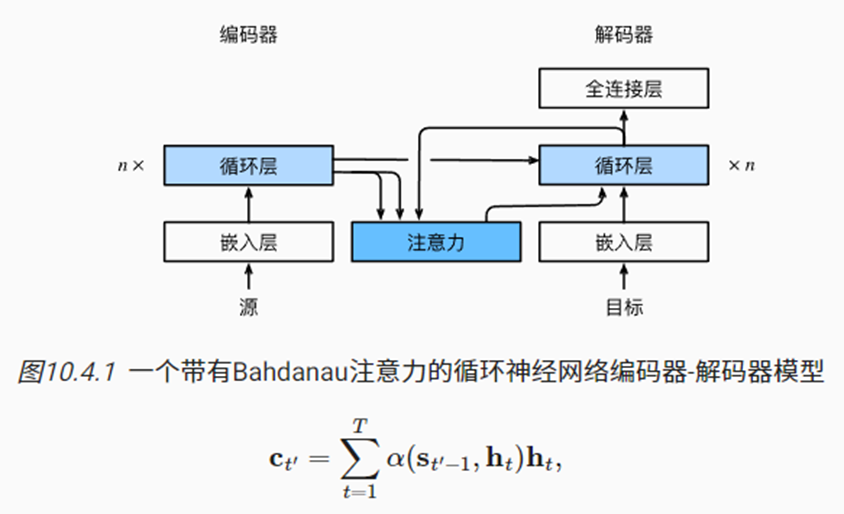
- 对此,Bahdanau等提出了注意力机制的seq2seq模型,具体实现方式如下:
4.1 模型
- 特定解码器词元的context上下文变量来自于编码器序列所有词元隐状态的加权平均
- Query:编码器RNN序列中,前一个时间步的最后一层隐状态输出
- Key/Value:解码器RNN序列中,每个时间步的最后一层隐状态输出(既作为Key,也作为Value)。
- 其它操作与之前学习基本一致。
|
|
4.2 定义注意力解码器
编码器不用重新定义,直接使用之前的就行
- 首先定义一个基本接口
|
|
- 然后是具体的代码实现
|
|
- 示例
|
|
4.3 训练
- 带有注意力机制的解码器会增加训练的时间
|
|
- 预测
- predict_seq2seq函数返回翻译后的outputs,以及相应的注意力权重结果
|
|
- 查看注意力权重
|
|
5. 多头注意力
5.1 模型
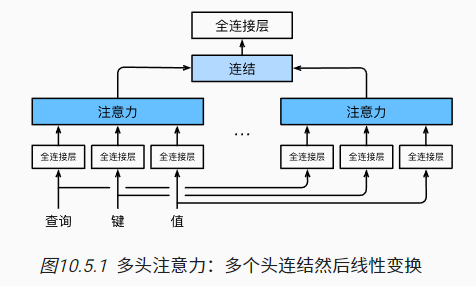
- 类似于CNN的多输出通道,多头注意力旨在通过多个独立的注意力汇聚学习到不同角度的信息
- 如下图所示:
- 首先将query,key,value向量进行线性投影(全连接层转换);
- 然后并行地分送到多个不同的注意力汇聚中;
- 最后将多头注意力输出结果拼接在一起,再经最后一个线性投影转换。
5.2 实现
- 通常选择缩放点积注意力作为每个注意力头;
|
|
- 如上操作,虽然是多头计算,但可以通过数据处理技巧节省运算。
- 简单来说,在计算式,通过合并num_head维度到batch_size维度,一次性计算多头的注意力结果。
- 最后再将结果在num_hiddens维度cat拼接到一起。
|
|
- 示例演示
- 5个注意力头
- qkv隐藏层神经元长度都设置为一样,为100
- 批量大小为2,每个批量4次query,6个键值对
|
|
6. 自注意力和位置编码
6.1 自注意力
- 可采用自注意力机制对序列词元进行编码。此时Query,以及Key-Value都来自同一组输入
- 即每个词元查询都会关注所有的键-值对,并生成一个注意力输出
|
|
6.2 比较CNN, RNN, Self-attention
卷积神经网路、循环神经网络,以及自注意力架构都可以将n个词元组成的序列映射到另一个长度相同的序列表示。
-
CNN (假设卷积核大小为k,输入与输出通道为d)
- 计算复杂度:O(knd*d)
- 顺序操作:O(1)
- 最大路径长度:O(n/k)
-
RNN(d×d权重矩阵,d维隐状态)
-
计算复杂度:O(d*d)
-
顺序操作:O(n)
-
最大路径长度:O(n)
-
-
Self-attention
-
计算复杂度:O(n*nd)
-
顺序操作:O(1)
-
最大路径长度:O(1)
-
综上:卷积神经网络和自注意力都拥有并行计算的优势。而自注意力的最大路径长度最短,其计算复杂度在很长的序列中计算会比较慢。
TIPS: 顺序操作会妨碍并行计算。而任意的序列位置组合之间的路径越短,则能更轻松地学习序列中的远距离依赖关系。
6.3 位置编码
- 在6.1的计算过程中,忽略了序列所包含的位置信息。
- 对于n×d的序列词元输入信息,可进行位置编码生成相同形状的表示,再进行矩阵加法,共同作为输入。
- n表示序列中词元的个数,d表示features数
- 如下公式,一种常见方式是基于正弦函数和余弦函数的固定位置编码。
- 序列中第i个词元(行)的第偶数个维数(列)使用sin函数
- 序列中第i个词元(行)的第奇数个维数(列)使用cos函数
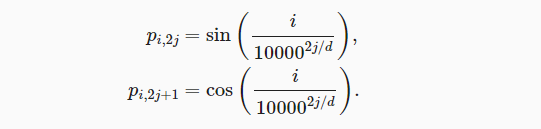
|
|
- 如下可视化,可以看出
- 第2j列与第2j+1列的周期/频率是一样的
- j越大,sin/cos函数周期越大,或者说频率越低
|
|
7. Transformer
- Transformer模型完全基于注意力机制,没有任何卷积层或循环神经网络层 (Attention is all you need);
- 它最初是应用于在文本数据上的序列到序列学习,但现在已经推广到各种现代的深度学习中,例如语言、视觉、语音和强化学习领域。
7.1 模型
- Transformer是一个经典的编码器与解码器架构。
架构角度
- 编码器:n个编码层组成,每个层由2个子层串联组成。每个子层后面都采用了残差连接,再应用层规范化(layer normalization)
- 第一个子层:多头自注意力汇聚;
- 第二个子层:基于位置的前馈网络;
- 解码器:n个解码层组成,每个层由3个子层串联组成。每个子层后面同样都采用了残差连接,再应用层规范化(layer normalization)
- 第一个子层:带掩码的多头自注意力汇聚;
- 第二个子层:编码器-解码器注意力层;
- 第三个子层:基于位置的前馈网络
数据角度
- 编码器
- 输入词元序列的embedding加上位置编码,输入到第一个编码层的第一个子层;
- 经过n层编码层学习后,输出的形状一般不变(batch_size, num_steps, num_hiddens)
- 解码器
- 标签词元序列的embedding,加上位置编码,输入到第一个解码层的第一个子层(掩码自注意力);
- 在第二个子层中,将第一个子层的输出作为Query,将编码器的输出作为Key和Value,进行解码,输出到前馈网络;
- 经过如上n个解码层学习,最后输出到一个全连接层中。
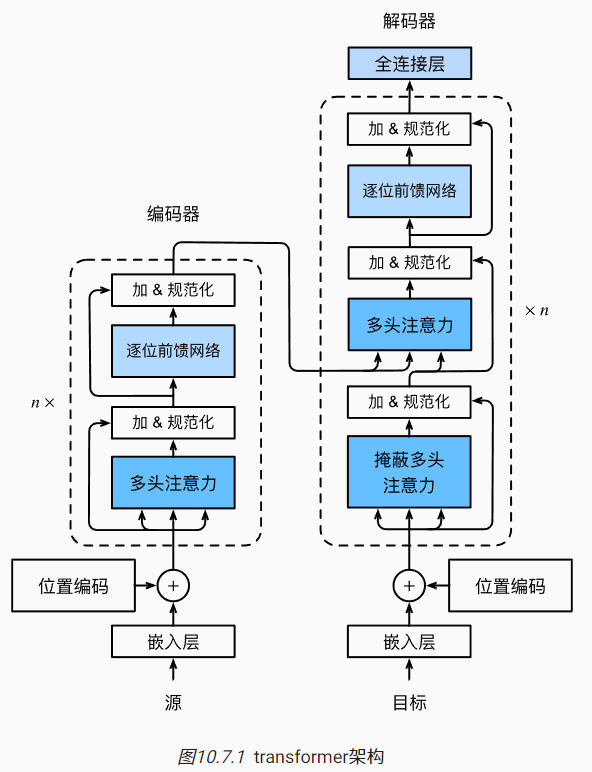
|
|
7.2 基于位置的前馈神经网络
- Positionwise feed-forward network, FFN
- 对序列中的每个位置词元特征,都进行相同的映射变换
- 本质上就是两层的MLP
- 输入形状:(批量大小,序列长度,特征维度)
- 输出形状:(批量大小,序列长度,特征维度2)
- FFN类的参数
- 输入:特征维度
- 中间:隐藏层神经元
- 输出:特征维度2
|
|
7.3 残差连接和层规范化
- 层规范化,Layer Normalization
- 对每个序列中所有词元的特征数据进行规范化
- e.g. 对于每个序列的二维矩阵(序列长度,特征数)的整体求均值与方差
TIPS: 之前学习的BatchNorm是对一个特征在所有批量样本的规范化。
|
|
- 残差连接的定义仍是加上原始输入X,以便计算深层网络
|
|
7.4 编码器
- 首先定义编码层,如上所述包含了两个子层
|
|
示例
|
|
- 构造编码器类
- 输入X加上位置编码,输入到n个编码层中得到输出
- num_layers设置n
|
|
示例
|
|
7.5 解码器
-
相对编码器,解码器的构造比较复杂。(1)每个解码层包括3个子层;(2)将编码器的输出结合到解码器中;(3)训练与预测的处理方式有差异
-
关于第一个子层,即带掩码的自注意力层:
-
在训练时,序列中所有位置的词元理论上都是已知的。
-
但是在真实的应用/预测场景中,只有生成的词元才能用于解码器的自注意力计算中。
-
dec_valid_lens参数可以使得查询都只会与解码器中所有已经生成词元的位置进行注意力计算。
-
-
关于第二个子层,即编码器-解码器注意力层
- 上一的解码层子层的单个词元输出将作为Query
- 来自编码器的输出将同时作为Key和Value
|
|
示例
|
|
- 构造解码器类
- 最后一个全连接层输出序列中每个词元的vocab_size个可能输出词元的概率
|
|
7.6 训练
- 同样以之前的’英语-法语’的机器翻译任务为例,演示Transformer的训练
|
|
尽管Transformer架构是为了序列到序列的学习而提出的,但正如本书后面将提及的那样,Transformer编码器或Transformer解码器通常被单独用于不同的深度学习任务中。