1. 门控循环单元(GRU)
传统的RNN在处理长序列时会遇到梯度消失或梯度爆炸的问题。为了解决这些问题,引入了门控机制的变种,如长短时记忆网络(LSTM, long short-term memory)和门控循环单元(GRU, gated recurrent unit)。GRU是LSTM的一个简化版本,它通过合并某些门并减少参数数量来提高效率。
1.1 门控隐藏状态
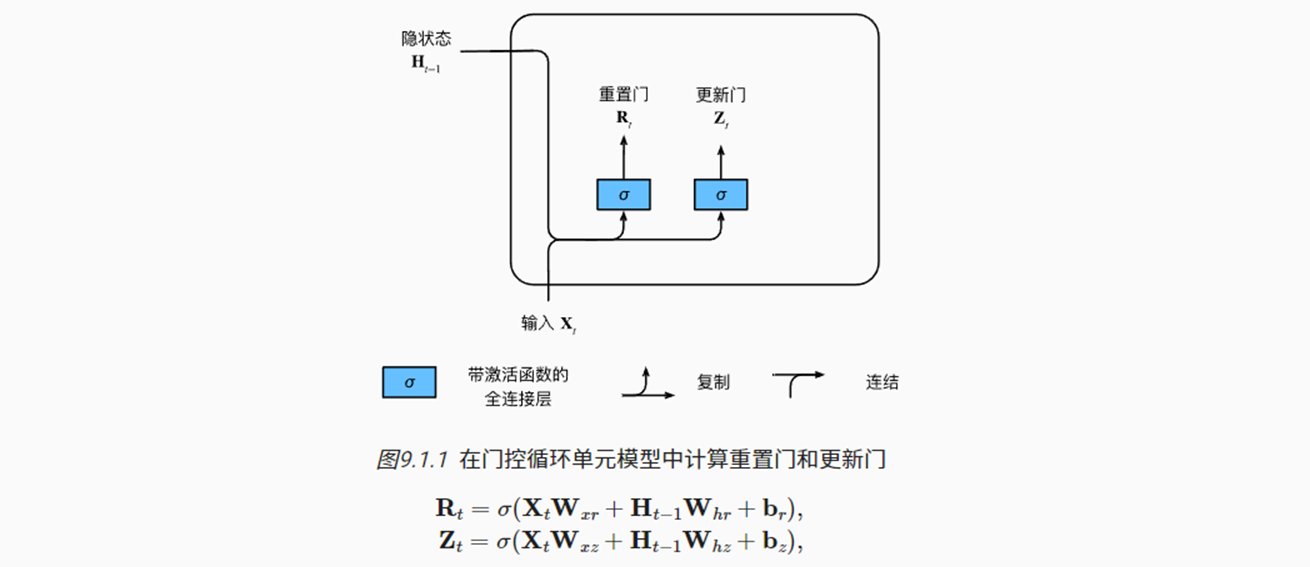
(1)重置门与更新门
通过支持对隐状态的门控,模型可以学习序列中相对重要的词元,跳过不太相关的词元。GRU包括了两个门控单元:
- 重置门:决定上一时刻的隐藏状态(Ht−1)有多少信息需要被“重置”或忽略,计算候选隐状态;
- 更新门:决定多少旧状态(Ht-1)应该被保留,多少新状态(即上面的候选隐状态,包括新输入的Xt)应该被添加到当前状态中。
- 计算上述两个门控单元的方式与RNN中Ht的计算公式基本一致,只是激活函数选择不同。这里使用的Sigmoid,使得转换为0~1范围,方便后续的控制操作。
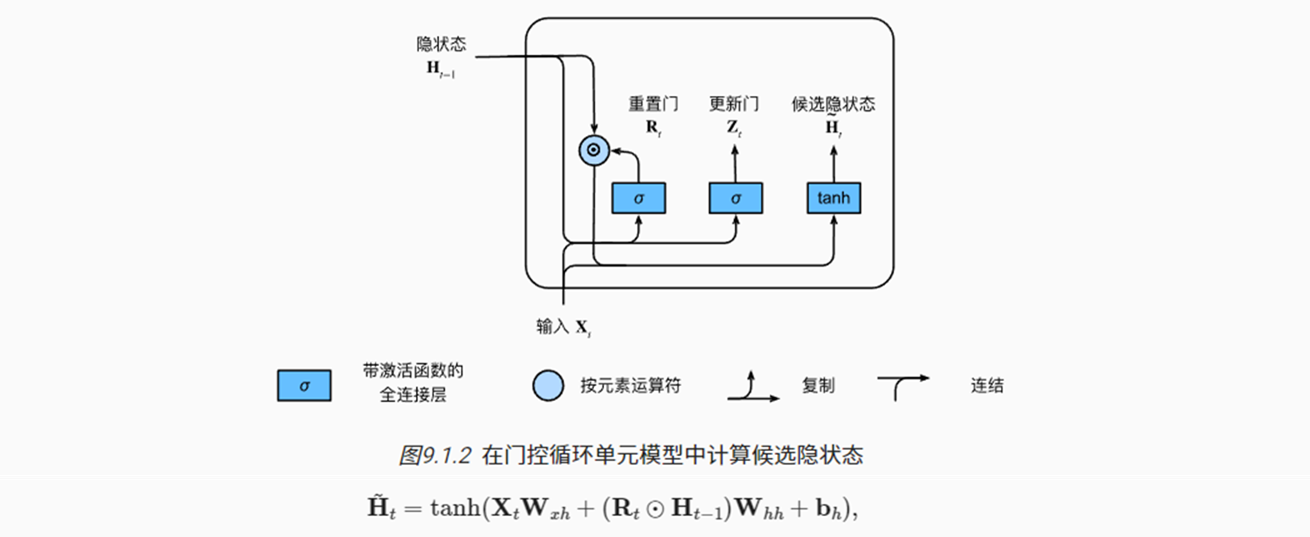
(2)候选隐状态
- 可通过重置门,来控制生成候选隐状态。
- Rt = 1时,就是基本的RNN层(包含Ht-1与Xt);
- Rt = 0时,上一步的隐状态会被重置/忽略,仅考虑Xt输入。
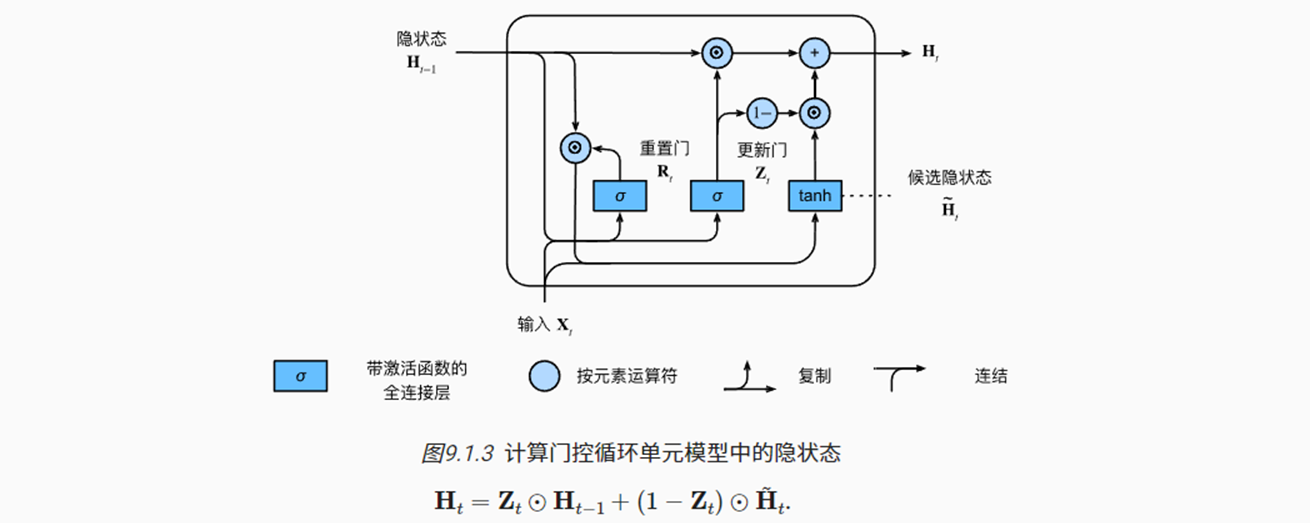
(3)隐状态
- 更新门可以控制最终隐状态的输出,用于预测Ot
- Zt = 0时,会全部使用上述的候选隐状态(包含Xt)
- Zt = 1时,会丢弃候选隐状态,直接继承前一隐藏状态的Ht-1
- 若整个子序列的所有时间步的更新门都接近1,则序列起始时间步的隐状态将很容易保留、并传递到序列结束。
综上,
- 重置门可以控制多大程度获得上一步骤的隐状态,有助于捕获序列中的短期依赖关系。
- 更新门可以控制多大程度学习当前步骤(Xt)的观测,有助于捕获序列中的长期依赖关系。
1.2 从零开始实现
- 加载数据
|
|
(1)初始化模型参数
- 与RNN相比,多了更新门与重置门的模型参数
|
|
(2)定义模型
- 隐状态初始化函数,与之前RNN一样
|
|
- 定义GRU模型的传播,
@表示按元素相乘的矩阵乘法
|
|
- 训练预测,与RNN代码基本一致
|
|
1.3 简洁实现
- 直接通过torch的
nn.GRU()定义门控神经单元
|
|
2. 长短期记忆网络(LSTM)
LSTM与GRU较为类似,其被早提出20年,设计更加复杂一点
2.1 门控记忆元
- 除了隐状态以外,LSTM又提出了记忆元的概念。它与隐状态的形状相同,设计目的是用于记录更多的信息。
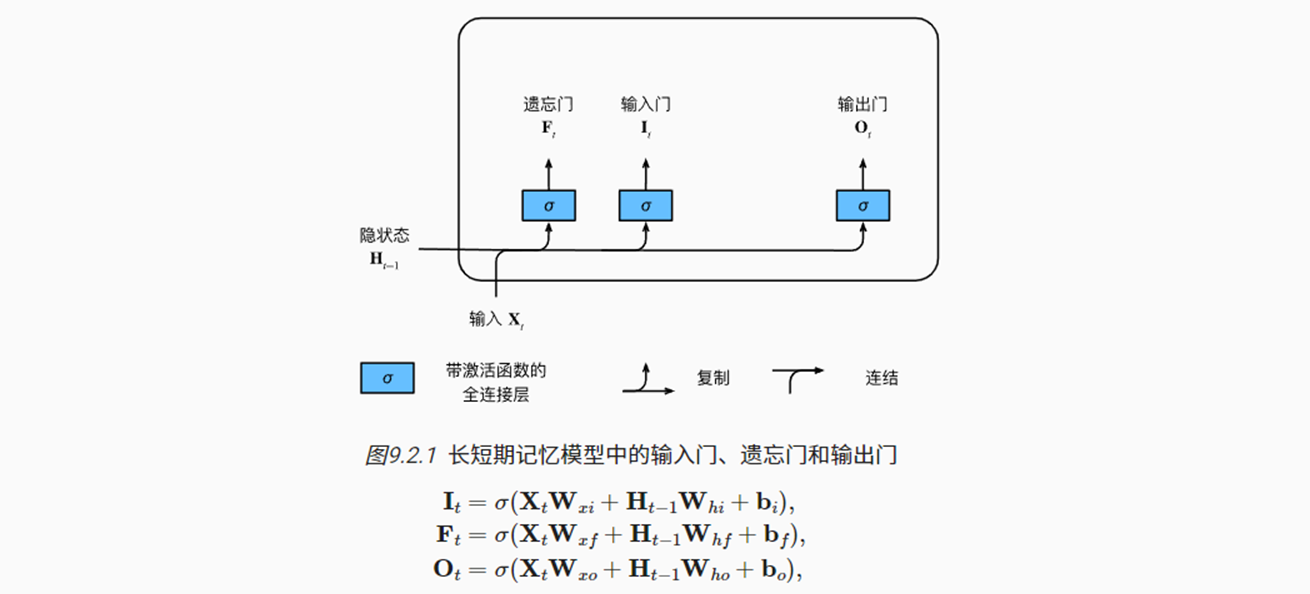
(1)输入门、输出门和输出门
- 共有三个门被提出用于控制记忆元:
- 输出门用来控制从记忆元输出到隐状态;
- 输入门用来控制如何从上一步的隐状态以及当前的观测中学习记忆元;
- 遗忘门用来控制多大程度继承上一步的记忆元。
- 这三个门的计算方式与之前都类似
(2)候选记忆元
- 候选记忆元的计算方式与上述也类似,只是激活函数为tanh,因此变换后的范围是(-1, 1)
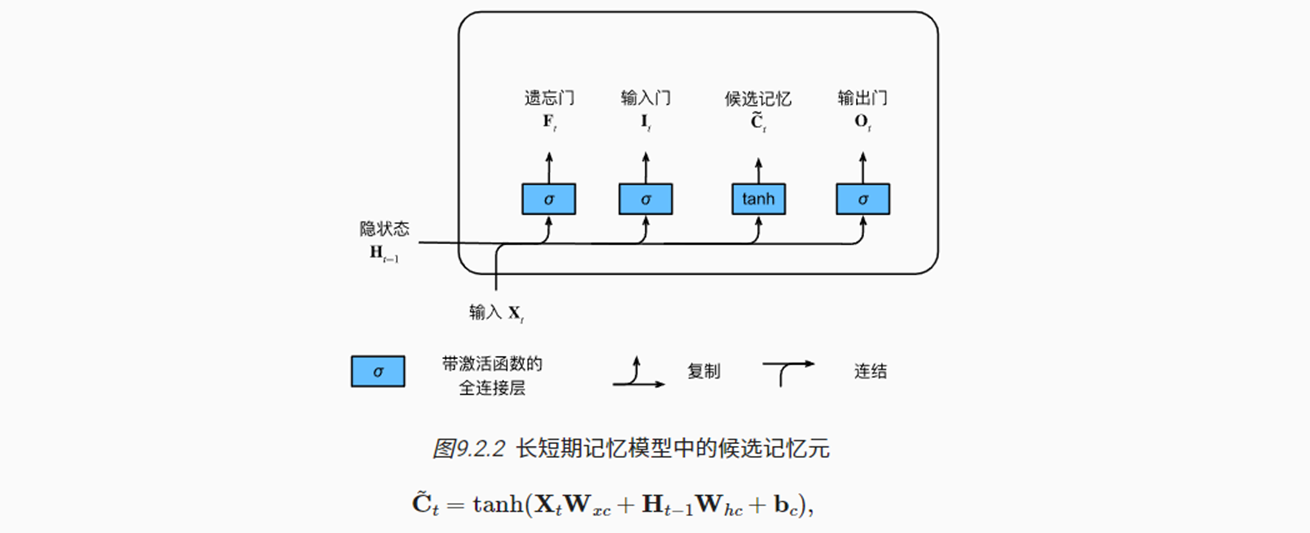
(3)记忆元
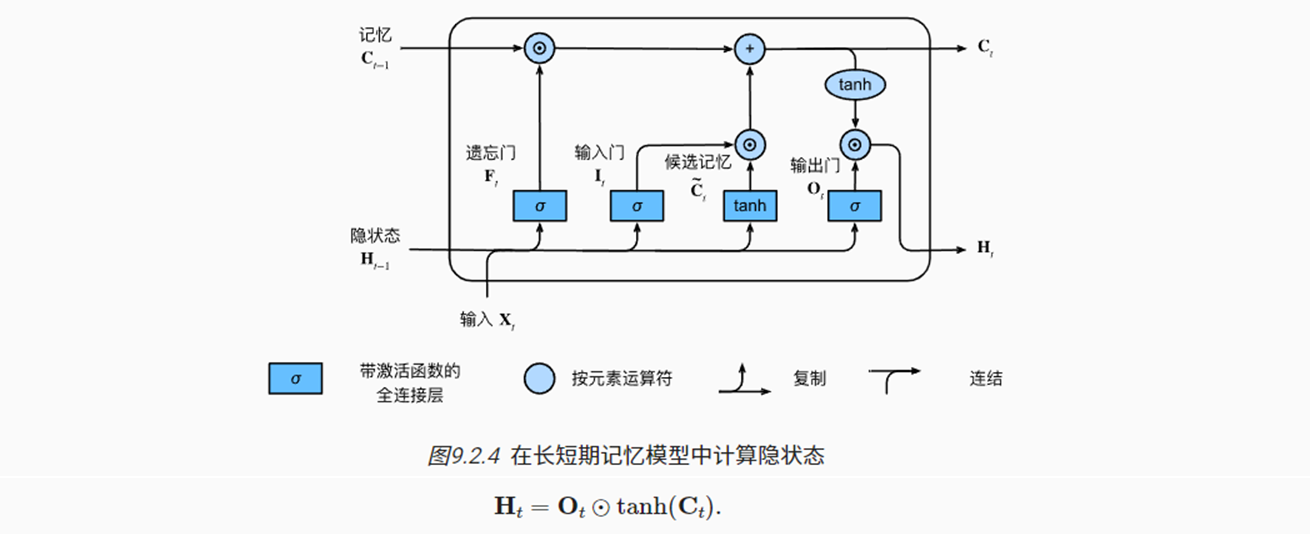
- 如下图,计算当前时间步的记忆元基于两个门的控制;
- 输入门It控制多大程度来自于上述计算的候选记忆元;
- 遗忘门Ft控制多大程度来自于上一时间步的记忆元;

(4)隐状态
- 基于上述的计算,最终通过输出门Ot决定多大程度将记忆元输出作为隐状态
2.2 从零开始实现
- 加载数据
|
|
(1)初始化模型参数
|
|
(2)定义模型
- 初始化隐状态以及记忆元,二者的形状相同
|
|
- 参照上述思路,定义LSTM的前向传播方式
|
|
(3)训练和预测
|
|
2.3 简洁实现
- 基于torch的
nn.LSTM(),快速实现
|
|
3. 深度RNN
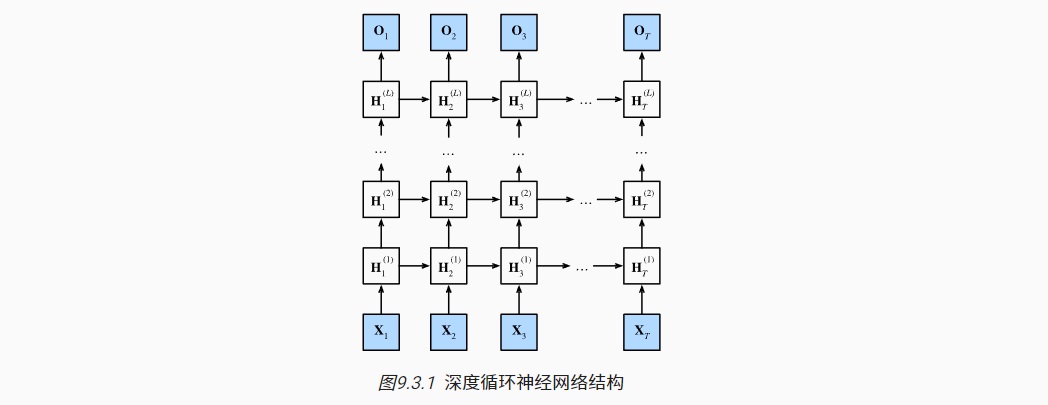
- 对于之前学习的RNN,以及更加复杂的GRU、LSTM,本质上都可以理解为单隐藏层(Ht)的MLP。
- 可以搭建具有L个隐藏层的深度循环神经网络, 每个隐状态都连续地传递到当前层的下一个时间步和下一层的当前时间步。
3.1 简洁实现
- 加载数据
|
|
- 如下以LSTM模型为例,仅需要在
nn.LSTM()模型中的第三个参数中设置层数即可
|
|
3.2 训练与预测
|
|
4. 双向RNN
4.1 定义
-
有时,序列的下文也对当前步的预测有帮助,例如
我__, 请给我点吃的。 -
双向RNN可以理解为有两个隐藏层的RNN模型,使用序列两端的信息预测输出。
- 其中两层遍历序列的方向相反,分别计算前向与反向隐状态
- 最后将两个隐状态结果合并起来,共同用于计算Ot
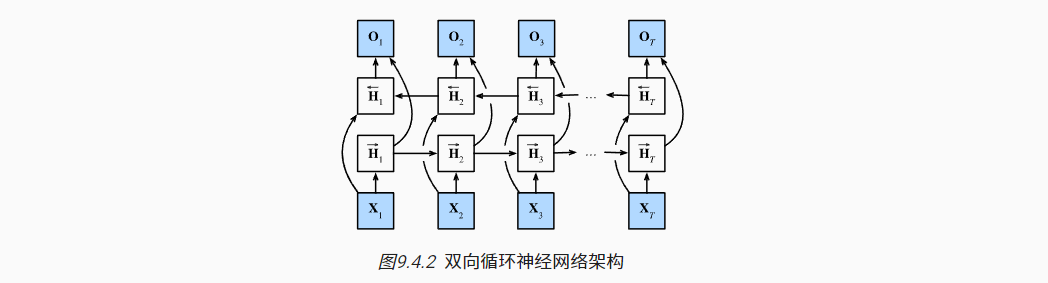
- 双向RNN模型的计算速度较慢,主要原因是网络的前向传播需要在双向层中进行前向和后向递归, 并且网络的反向传播还依赖于前向传播的结果。 因此,梯度求解将有一个非常长的链。
- 此外,双向RNN模型的应用场景有限,不适合用于下文预测;可以用于填充缺失的单词、词元注释,机器翻译等。
4.2 错误应用
- 如上,双向RNN在预测时需要用到过去和未来的数据,不适合用于预测未来词元,尽管有时模型训练性能较好。
- 在torch中实现也很简单,仅需要设置相应的参数即可。
|
|
5. 机器翻译与数据集
- 机器翻译是将一种语言翻译为另一种语言;
- 可以理解为是将输入序列转换成输出序列的序列转换模型。
- 接下来的后面几节都将学习如何实现
|
|
5.1 下载和预处理
- 示例数据是一个’英语—法语’文本数据集。
- 每一行都是由制表符分割的文本序列对。
- 文本序列可以是单词,句子,段落(包含标点)
|
|
- 文本预处理操作
|
|
5.2 词元化
- 将单词以及标点符号认为是词元
- 在每一行中,对制表符前后的文本分别进行词元化,作为source与target
|
|
5.3 词表
- 分别为源语言(英语)以及目标(法语)语言构建词表;
- 将词频低于2的词元设置为’<unk>'
- 此外,额外指定几个特殊词元
- ‘<pad>’ 填充词元
- ‘<bos>’ 开始词元
- ‘<eos>’ 结束词元
|
|
5.4 加载数据集
- 为了便于训练,需要将输入序列为设置为固定长度。此时会有如下两种情况
- 截断:仅取前面预期序列长度的词元,丢弃后面的词元
- 填充:当不满足预期序列长度时,在后面填充补齐
|
|
- 定义一个函数,对source/target进行上述处理,并在序列结尾加上一个’<eos>‘词元
- 此外,会统计一下每个序列的有效长度(除去填充词元)
|
|
5.5 最终形式
- 定义一个综合函数,返回数据迭代器,源语言词表,目标语言词表
- 数据迭代器每次返回一个批量的输入序列与输出序列
|
|
- 示例
|
|
6. 编码器与解码器架构
- 对于之前学习的CNN以及现在学习的RNN,都可以理解为编码器与解码器架构;
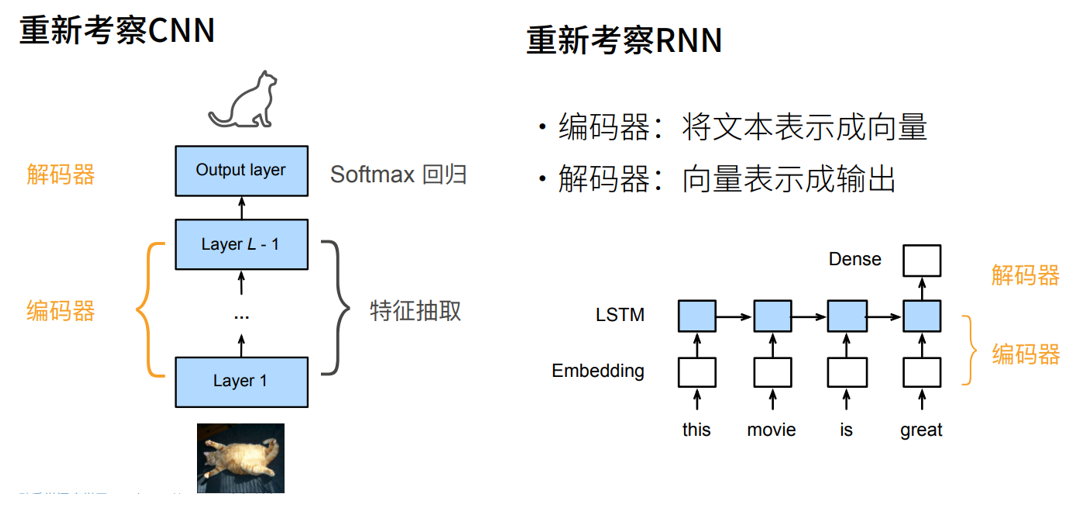
- 编码器:将输入变换为中间表达形式(特征);
- 对于RNN,可将长度可变的序列作为输入,转换为具有固定形状的编码状态
- 解码器:将提取的中间表示编码成输出。
- 对于RNN,将固定形状的编码状态映射到长度可变的序列

接下来定义一个抽象的编码器-解码器接口,以方便后续的实现
6.1 编码器
- 在编码器接口中,指定长度可变的序列作为输入X
|
|
raise NotImplementedError是一种编程模式,用于表明某个方法或功能还没有准备好或者需要被子类覆盖以提供实际的行为。
6.2 解码器
init_state用于初始化解码器的状态。- 主要是将编码器的输出转换为编码后的状态
- 根据RNN思路,解码器在每个时间步都会将输入X (例如:在前一时间步生成的词元)和编码后的状态 映射成当前时间步的输出词元。
|
|
6.3 合并编码器与解码器
在前向传播中,
- 编码器的输出用于生成编码状态;
- 这个状态又被解码器作为其输入的一部分。
|
|
7. 序列到序列学习(seq2seq)
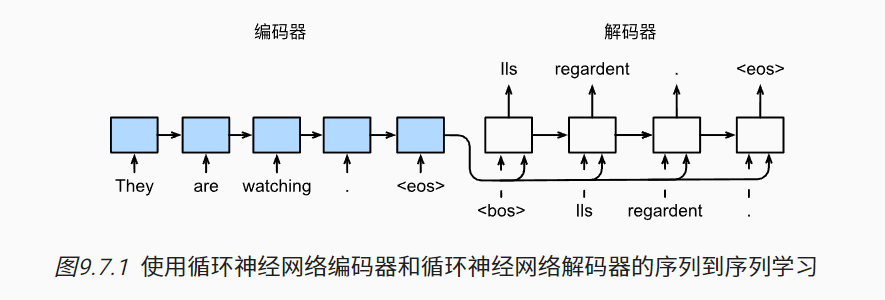
- 序列到序列学习模型由两个RNN的编码器与解码器组成
- 编码器RNN:将输入序列的信息编码为固定形状的隐状态。
- 解码器RNN:基于编码器输入序列的编码信息以及当前时间步的词元,来预测下一个词元。
|
|
7.1 编码器
- 在编码器RNN部分,主要目的是得到输入序列最后一个时间步的隐状态表示(可以有多层)。
|
|
output是基于每个时间步最后一层的隐状态(一般情况下后面需要跟全连接层进行预测输出);
state是最后一个时间步的多层的隐状态。
- 示例
|
|
7.2 解码器
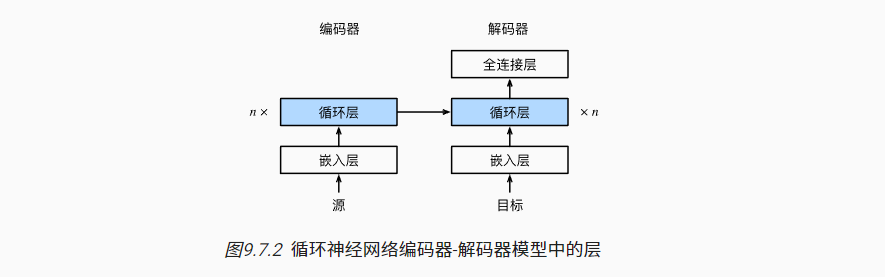
在解码器RNN中,
- 一方面,会继承编码器RNN的最后一个时间步的所有隐状态,作为解码器输入序列的初始化隐状态;
- 另一方面会将编码器RNN的最后一个时间步的最后一层隐状态,作为解码器输入序列中每个观测词元的一部分特征(参考上图)。
|
|
7.3 损失函数
- 对于解码器的预测输出,一般使用平均交叉熵损失(Softmax)评价与标签序列的差异损失;
- 在计算损失时,应不需要关注对于序列中的填充词元的预测正确与否
- 换句话说,仅关注序列中有效词元的预测结果
|
|
- 据此自定义一个损失函数
|
|
7.4 训练
- 在解码器中,’<bos>‘与原始的输出序列(不包含’<eos>’)连接在一起共同作为输入。
|
|
- 实例化模型,并训练
|
|
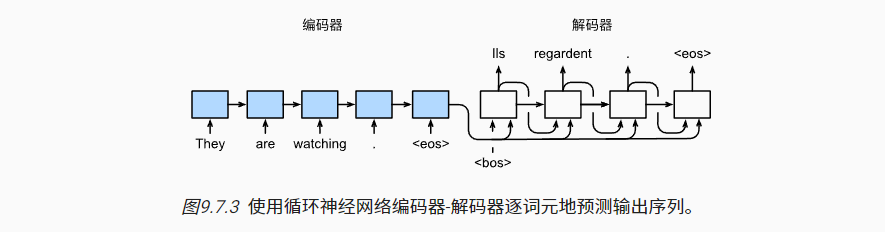
7.5 预测
- 与训练部分不同之处在于, 每个解码器当前时间步的输入都将来自于前一时间步的预测词元。而在训练时的解码器输入都是来自真实的词元。
- src_sentence 表示用户的输入英语句子
- src_vocab表示英语的索引词表
- tgt_vocab表示法语的索引词表
|
|
7.6 预测序列的评估
- 可使用Bleu值评估预测序列与真实序列的差异;值越大,且接近1表示效果越好
- 当预测的序列长度小于真实序列长度时,前面的exp系数运算就会小于1,即对Bleu值惩罚;
- 当n值较大时的n元预测准确率越高时,Pn项就越大。
具体地说,给定标签序列A、B、C、D、E、F 和预测序列A、B、B、C、D, 我们有p1=4/5、p2=3/4、p3=1/3和p4=0。
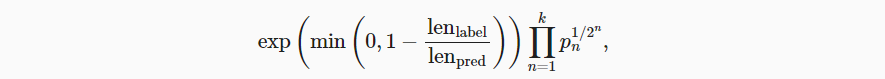
|
|
- 示例
|
|