1. 深度卷积神经网络(AlexNet)

1.1 学习表征

LeNet提出后，卷积神经网络并未占据主流，而是往往由其它机器学习方法所超越，如SVM。一个主要的原因是输入数据的特征处理上。

CNN模型是基于端到端的预测，由模型本身来学习、提取特征。例如直接从图片像素到分类结果的预测；
SVM等经典机器学习模型则依赖于精细的特征工程，即使用经过人的手工精心设计的特征来建模。

在2012年，AlexNet模型取得了当年ImageNet挑战赛的冠军，标志着深层神经网络相关研究的起点。

在CNN的底层（例如第一层、第二层等）中的每一个通道可以’理解’为对某种模式特征的提取表示，用于更高层的综合学习。

此外，限制神经网络取得良好性能的因素还包括数据与硬件两方面——

数据：深度模型需要大量的有标签数据才能显著优于基于凸优化的传统方法（如线性方法和核方法）
- 2009年，由斯坦福教授李飞飞小组发布了ImageNet数据集，并发起ImageNet挑战赛：要求研究人员从100万个样本中训练模型，以区分1000个不同类别的对象。
硬件：深度学习模型对计算资源要求很高，需要数百次迭代训练；每次迭代有需要许多线性代数层传递数据。
- 相比于CPU，GPU用于大量的计算核心，方便并行运算；此外也提供更高的浮点运算性能（FLOPS），并配备有高带宽的显存（VRAM）等优势。

1.2 AlexNet

本书在这里提供的是一个稍微精简版本的AlexNet

AlexNet与LeNet架构非常相似，在以下方面进行了提升：

模型设计：由8层组成，包括5个卷积层、3个全连接层
- 考虑ImageNet图像宽高显著多于MNIST，第1个卷积层的卷积核窗口为11×11，第二个为5×5，往后都是3×3；
- 卷积输出通道数也是LeNet的10倍以上；
- 在第1、第2、第5层卷积层后加入最大汇聚层；
- 两个全连接隐藏层有4096个输出，用于接近1GB的模型参数；
激活函数：使用ReLU激活函数相比于Sigmoid计算更加简单，且更适应多种参数初始化方法。
容量控制：使用Dropout暂退法控制了全连接层的模型复杂度。

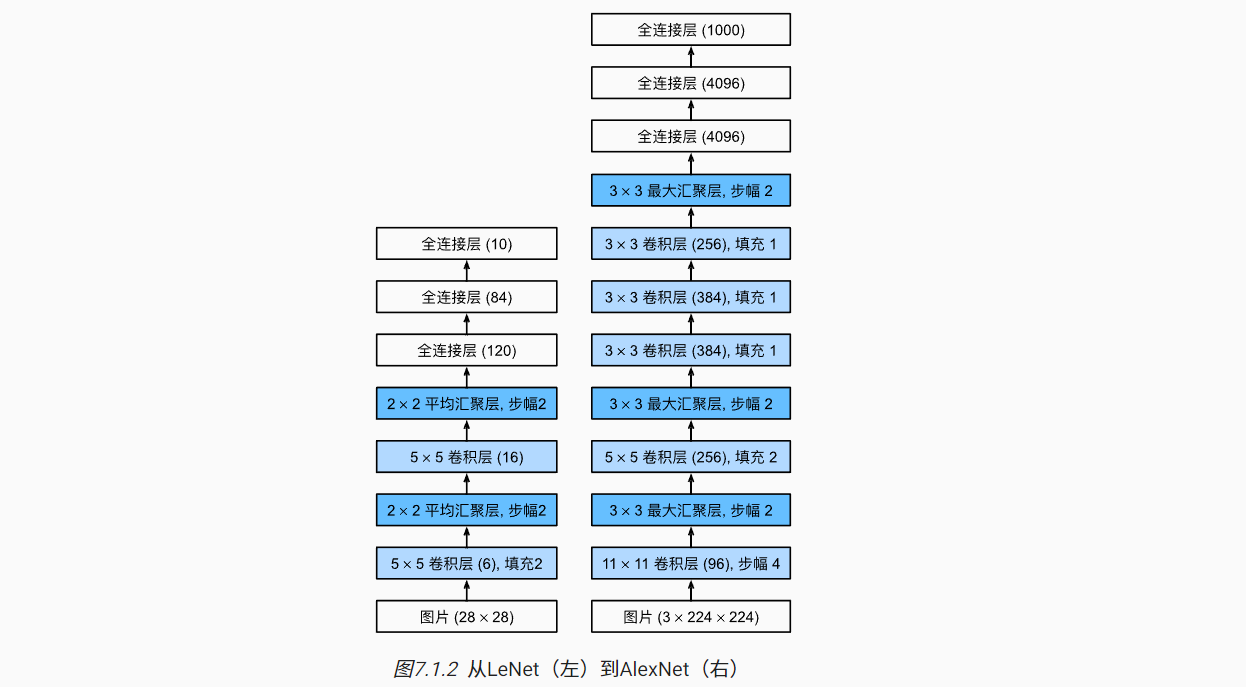
如下的模型架构是为Fashion-MNIST数据集修改后的设计，主要体现在第一层卷积层的输入通道数为1。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


import torch
from torch import nn
from d2l import torch as d2l

net = nn.Sequential(
    # 这里使用一个11*11的更大窗口来捕捉对象。
    # 同时，步幅为4，以减少输出的高度和宽度。
    # 另外，输出通道的数目远大于LeNet
    nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 减小卷积窗口，使用填充为2来使得输入与输出的高和宽一致，且增大输出通道数
    nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    # 使用三个连续的卷积层和较小的卷积窗口。
    # 除了最后的卷积层，输出通道的数量进一步增加。
    nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
    nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2),
    nn.Flatten(),
    # 这里，全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过拟合
    nn.Linear(6400, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    nn.Linear(4096, 4096), nn.ReLU(),
    nn.Dropout(p=0.5),
    # 最后是输出层。由于这里使用Fashion-MNIST，所以用类别数为10，而非论文中的1000
    nn.Linear(4096, 10))

以一个高度和宽度都为224的单通道输入数据为例

1
2
3
4


X = torch.randn(1, 1, 224, 224)
for layer in net:
    X=layer(X)
    print(layer.__class__.__name__,'output shape:\t',X.shape)

1.3 读取数据集

为了将Fashion-MNIST数据用于AlexNet模型框架，需要将像素分辨率重新设置为224×224

1
2


batch_size = 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)

1.4 训练AlexNet

1
2
3
4


lr, num_epochs = 0.01, 10
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
# loss 0.333, train acc 0.879, test acc 0.849
# 5523.8 examples/sec on cuda:0

2 使用块的网络(VGG)

AlexNet虽然证明深层网络有效，但未能提供通用的模板指导后续的设计；
VGG由牛津大学的视觉几何组于2013年提出，可以简洁地实现更深更窄的网络，在2014年ImageNet中取得优异的表现。

2.1 VGG块

VGG块提出了一种经典的卷积神经网络的组成架构，包括如下：

多个连续的卷积层
- 较小的3×3卷积核；
- 带填充以保持输出分辨率不变；
- 自定义输出通道。
ReLU激活函数；
步幅为2的2×2最大汇聚层，使得输出高宽减半

代码实现如下，可调整参数包括：

num_convs 块包含多少个卷积层；
in_channels 输入通道数
out_channels 输出通道数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


import torch
from torch import nn
from d2l import torch as d2l


def vgg_block(num_convs, in_channels, out_channels):
    layers = []
    for _ in range(num_convs):
        layers.append(nn.Conv2d(in_channels, out_channels,
                                kernel_size=3, padding=1))
        layers.append(nn.ReLU())
        in_channels = out_channels
    layers.append(nn.MaxPool2d(kernel_size=2,stride=2))
    return nn.Sequential(*layers)

2.2 VGG网络

参考AlexNet，VGG同样可以分为两部分：

第一部分由多个VGG块组成的卷积层部分；
第二部分由3个的全连接层组成。

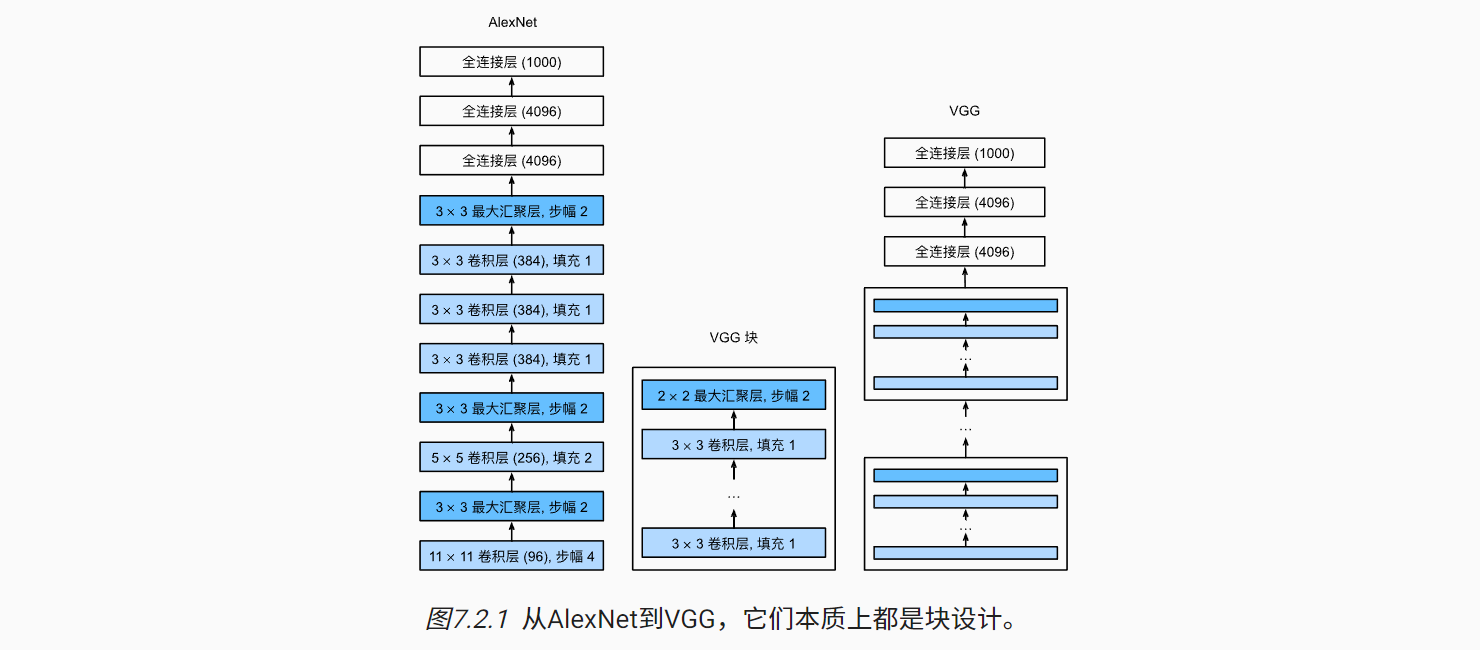
原始VGG网络包含如下5个VGG块，共有5个卷积层；结合三个全连接层，因此又称为VGG-11。

第一个块：1个卷积层，64个输出通道；
第二个块：1个卷积层，128个输出通道；
第三个块：2个卷积层，256个输出通道；
第四个块：2个卷积层，512个输出通道；
第五个块：2个卷积层，512个输出通道；

1

conv_arch = ((1, 64), (1, 128), (2, 256), (2, 512), (2, 512))

由于每个块的最后一层都是最大汇聚层，使得输出减半；同时增加输出通道数。这是经典的CNN设计思路。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


def vgg(conv_arch):
    conv_blks = []
    in_channels = 1  #Fashion-MNIST通道数为1
    # 卷积层部分
    for (num_convs, out_channels) in conv_arch:
        conv_blks.append(vgg_block(num_convs, in_channels, out_channels))
        in_channels = out_channels #前者的输出通道数等于后者的输入通道数

    return nn.Sequential(
        *conv_blks, nn.Flatten(),
        # 全连接层部分
        # 224/2/2/2/2/2 = 7
        nn.Linear(out_channels * 7 * 7, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096, 4096), nn.ReLU(), nn.Dropout(0.5),
        nn.Linear(4096, 10))

net = vgg(conv_arch)

X = torch.randn(size=(1, 1, 224, 224))
for blk in net:
    X = blk(X)
    print(blk.__class__.__name__,'output shape:\t',X.shape)

2.3 训练模型

由于VGG-11比AlexNet计算量更大，因此这里构建了一个通道数较少的网络

1
2
3
4
5
6
7
8
9


ratio = 4
small_conv_arch = [(pair[0], pair[1] // ratio) for pair in conv_arch]
net = vgg(small_conv_arch)

lr, num_epochs, batch_size = 0.05, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
# loss 0.174, train acc 0.936, test acc 0.908
# 3872.4 examples/sec on cuda:0

3. 网络中的网络(NiN)

在前述介绍的网络组成中，在最后通常会加入全连接层，会导致引入大量的模型参数；
1×1卷积核可以起到混合通道的作用，有点类似MLP的全连接层；
NiN网络在AlexNet的基础之上，使用了1×1卷积核，取代了上述全连接层部分的作用。

3.1 NiN块

NiN块提出了一种特殊的组成架构，包括如下：

第一层为用户自定义的卷积层，以及ReLU激活函数；
第二、三层为1×1卷积核的卷积层，输出通道数不变，同样分别加入ReLU激活函数；

使用1×1卷积核时，相当于对同一位置，不同通道的元素进行全连接层

代码实现如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


import torch
from torch import nn
from d2l import torch as d2l

def nin_block(in_channels, out_channels, kernel_size, strides, padding):
    return nn.Sequential(
        nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
        nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())

3.2 NiN模型

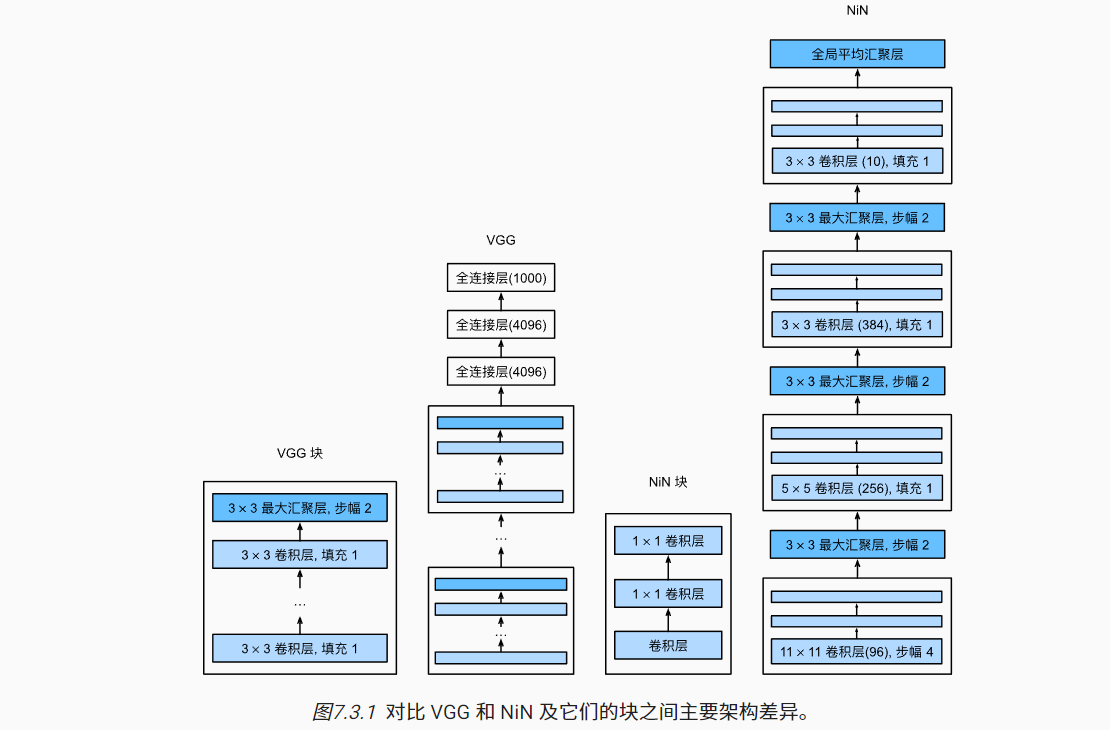
由4个NiN块组成，每个NiN块中的卷积核窗口参考AlexNet设置为11×11，5×5，3×3，3×3
前3个NiN块后接一个最大池化层；
最后一个NiN块的输出通道数等于类别数，且后面接一个全局平均池化层，输出为1×1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


net = nn.Sequential(
    nin_block(1, 96, kernel_size=11, strides=4, padding=0),
    nn.MaxPool2d(3, stride=2),
    nin_block(96, 256, kernel_size=5, strides=1, padding=2),
    nn.MaxPool2d(3, stride=2),
    nin_block(256, 384, kernel_size=3, strides=1, padding=1),
    nn.MaxPool2d(3, stride=2),
    nn.Dropout(0.5),
    # 标签类别数是10
    nin_block(384, 10, kernel_size=3, strides=1, padding=1),
    nn.AdaptiveAvgPool2d((1, 1)),
    # 将四维的输出转成二维的输出，其形状为(批量大小,10)
    nn.Flatten())

X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t', X.shape)

3.3 训练模型

1
2
3
4
5
6


lr, num_epochs, batch_size = 0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)

d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
# loss 0.341, train acc 0.873, test acc 0.875
# 4756.1 examples/sec on cuda:0

4. 含并行连接的网络(GoogLeNet)

基于NiN中串联网络的思想，GoogLeNet在2014年ImageNet图像识别挑战赛的取得佳绩；

4.1 Inception块

如下图，Inception块由4条并行的路径组成，每个路径仅改变通道数，不改变高宽。

第一条：1×1卷积
第二条：1×1卷积，加上3×3卷积(填充1)
第三条：1×1卷积，加上5×5卷积(填充2)
第四条：3×3最大汇聚(填充1)，加上1×1卷积

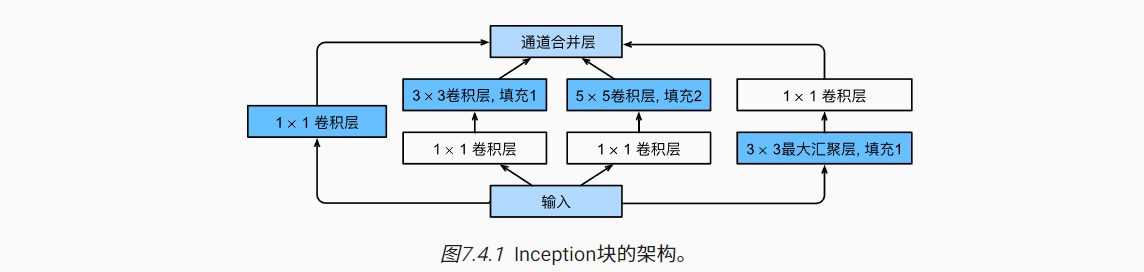
如下是定义Inception块的代码，其中可调参数均是输入以及每条路径中的通道数。

in_channels 输入通道数;
c1 第一条路径的输出通道数;
c2 第二条路径每个卷积层的输出通道数;
c3 第三条路径每个卷积层的输出通道数;
c4 第四条路径每个卷积层的输出通道数;

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l


class Inception(nn.Module):
    # c1--c4是每条路径的输出通道数
    def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):
        super(Inception, self).__init__(**kwargs)
        # 线路1，单1x1卷积层
        self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
        # 线路2，1x1卷积层后接3x3卷积层
        self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        # 线路3，1x1卷积层后接5x5卷积层
        self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        # 线路4，3x3最大汇聚层后接1x1卷积层
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)

    def forward(self, x):
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        # 在通道维度上连结输出
        return torch.cat((p1, p2, p3, p4), dim=1)

4.2 GoogLeNet模型

如下示意图，GoogLeNet模型共有5个部分组成(从下到上)：

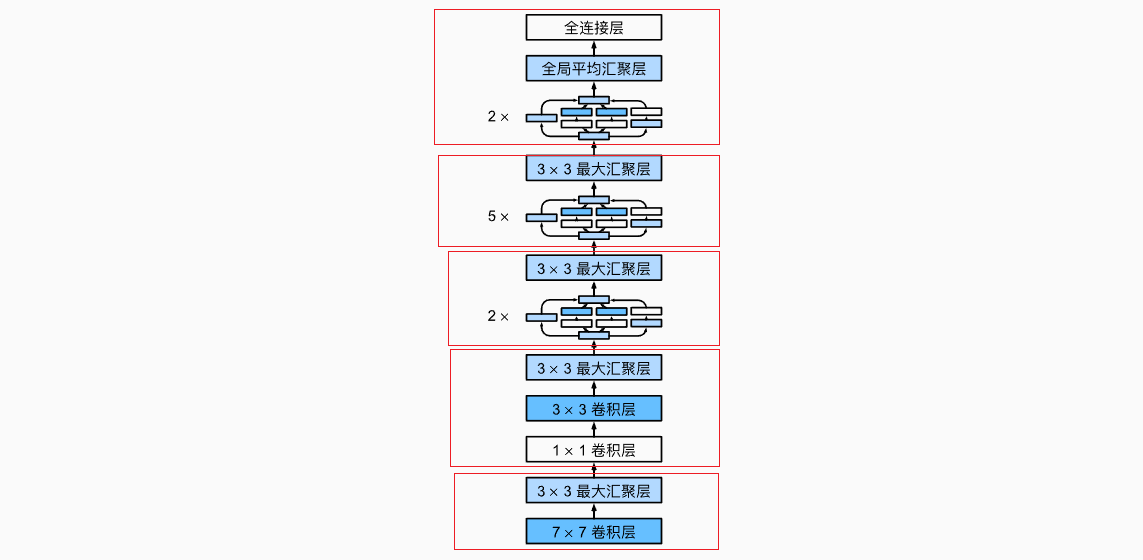
第一部分：类似于AlexNet，一个卷积层加上一个最大汇聚层；

1
2
3


b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

第二部分：两个卷积层加上一个最大汇聚层

1
2
3
4
5


b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1),
                   nn.ReLU(),
                   nn.Conv2d(64, 192, kernel_size=3, padding=1),
                   nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

第三部分：2个Inception块，加上最大汇聚层
- e.g. 第一个卷积层：输入通道=192，输出通道=64+128+32+32=256

1
2
3


b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32),
                   Inception(256, 128, (128, 192), (32, 96), 64),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

第四部分：5个Inception块，加上最大汇聚层
- e.g. 第一个卷积层：输入通道=480，输出通道=192+208+48+64=512

1
2
3
4
5
6


b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64),
                   Inception(512, 160, (112, 224), (24, 64), 64),
                   Inception(512, 128, (128, 256), (24, 64), 64),
                   Inception(512, 112, (144, 288), (32, 64), 64),
                   Inception(528, 256, (160, 320), (32, 128), 128),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

第五部分：2个Inception块，加上全局平均汇聚层以及全连接层
- e.g. 最后一层卷积层：输入通道=832，输出通道=384+384+128+128=1024
- 全局平均汇聚层以及Flatten将输出变为1024的特征向量，后面再根据类别数接一个全连接层

1
2
3
4
5
6


b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128),
                   Inception(832, 384, (192, 384), (48, 128), 128),
                   nn.AdaptiveAvgPool2d((1,1)),
                   nn.Flatten())

net = nn.Sequential(b1, b2, b3, b4, b5, nn.Linear(1024, 10))

查看模型架构（仍是高宽变小，通道数变多的思想）

1
2
3
4


X = torch.rand(size=(1, 1, 96, 96))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t', X.shape)

4.3 训练模型

1
2
3
4
5
6


lr, num_epochs, batch_size = 0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)

d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
# loss 0.249, train acc 0.905, test acc 0.827
# 3811.4 examples/sec on cuda:0

5. 批量规范化

加速深层神经网络的收敛

5.1 训练深层网络

批量规范化(Batch Normalization, BN)用于对特定神经网络层中，每次训练迭代的小批量输入数据进行’归一化’处理。
这使得不同层之间的参数量级得到统一，防止模型参数的更新是为了补偿不同层之间的数据差异，从而针对性的对预测问题本身进行学习，加速模型收敛。
具体实现其实也并不复杂：

（1）首先对一个小批量B，计算其（feature）均值与方差

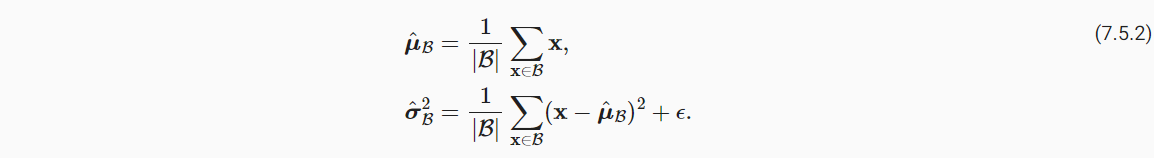
（2）然后，进行均值为0，方差为1的归一化处理后，进一步进行拉伸与偏移。γ可以变换方差，β可以变换均值，均属于可学习的参数，从而拟合最适合的规范化分布。

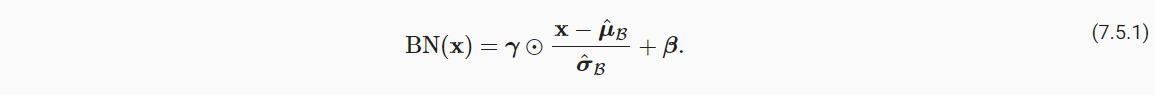
一种角度的解释是BN操作中会引入一定的噪声，控制了模型复杂度。因为随机抽样的小批量分布不能代表总体情况。

5.2 批量规范化层

对于全连接层：
- BN操作位于全连接层与激活函数之间；
- 对于[小批量数，特征数]的输入数据，会对每一列特征进行BN操作。即每个特征学习的γ与β都是不同的；
对于卷积层
- BN操作位于卷积层与激活函数之间；
- 对于多通道输出，会将每个通道作为一个特征，即计算小批量样本对于特定通道的，所有元素的均值与方差。
此外，BN操作在预测过程是估算特征在整个训练数据集的均值与方差，再进行规范化。

5.3 从零实现

首先定义一个函数，进行BN操作

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


import torch
from torch import nn
from d2l import torch as d2l

def batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):
    # 通过is_grad_enabled来判断当前模式是训练模式还是预测模式
    if not torch.is_grad_enabled():
        # 如果是在预测模式下，直接使用传入的移动平均所得的均值和方差
        X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)
    else:
        assert len(X.shape) in (2, 4)
        if len(X.shape) == 2:
            # 使用全连接层的情况，计算特征维上的均值和方差
            mean = X.mean(dim=0)
            var = ((X - mean) ** 2).mean(dim=0)
        else:
            # 使用二维卷积层的情况，计算通道维上（axis=1）的均值和方差。
            # 这里我们需要保持X的形状以便后面可以做广播运算
            mean = X.mean(dim=(0, 2, 3), keepdim=True)
            var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)
        # 训练模式下，用当前的均值和方差做标准化
        X_hat = (X - mean) / torch.sqrt(var + eps)
        # 更新移动平均的均值和方差
        moving_mean = momentum * moving_mean + (1.0 - momentum) * mean
        moving_var = momentum * moving_var + (1.0 - momentum) * var
    Y = gamma * X_hat + beta  # 缩放和移位
    return Y, moving_mean.data, moving_var.data

然后定义一个BatchNorm层

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


class BatchNorm(nn.Module):
    # num_features：完全连接层的输出数量或卷积层的输出通道数。
    # num_dims：2表示完全连接层，4表示卷积层
    def __init__(self, num_features, num_dims):
        super().__init__()
        if num_dims == 2:
            shape = (1, num_features)
        else:
            shape = (1, num_features, 1, 1)
        # 参与求梯度和迭代的拉伸和偏移参数，分别初始化成1和0
        self.gamma = nn.Parameter(torch.ones(shape))
        self.beta = nn.Parameter(torch.zeros(shape))
        # 非模型参数的变量初始化为0和1
        self.moving_mean = torch.zeros(shape)
        self.moving_var = torch.ones(shape)

    def forward(self, X):
        # 如果X不在内存上，将moving_mean和moving_var
        # 复制到X所在显存上
        if self.moving_mean.device != X.device:
            self.moving_mean = self.moving_mean.to(X.device)
            self.moving_var = self.moving_var.to(X.device)
        # 保存更新过的moving_mean和moving_var
        Y, self.moving_mean, self.moving_var = batch_norm(
            X, self.gamma, self.beta, self.moving_mean,
            self.moving_var, eps=1e-5, momentum=0.9)
        return Y

5.4 使用批量规范化层的LeNet

定义模型

1
2
3
4
5
6
7
8


net = nn.Sequential(
    nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2),
    nn.Conv2d(6, 16, kernel_size=5), BatchNorm(16, num_dims=4), nn.Sigmoid(),
    nn.AvgPool2d(kernel_size=2, stride=2), nn.Flatten(),
    nn.Linear(16*4*4, 120), BatchNorm(120, num_dims=2), nn.Sigmoid(),
    nn.Linear(120, 84), BatchNorm(84, num_dims=2), nn.Sigmoid(),
    nn.Linear(84, 10))

训练模型

1
2
3
4
5
6


lr, num_epochs, batch_size = 1.0, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
# loss 0.272, train acc 0.899, test acc 0.863
# 23764.9 examples/sec on cuda:0

查看模型BN层的γ与β参数

1
2
3
4
5


net[1].gamma.reshape((-1,)), net[1].beta.reshape((-1,))
# (tensor([3.3490, 3.2102, 4.1508, 1.7645, 2.7210, 0.5482], device='cuda:0',
#         grad_fn=<ViewBackward0>),
#  tensor([ 0.3007,  2.3391,  4.3099, -0.4318, -0.8200, -0.5383], device='cuda:0',
#         grad_fn=<ViewBackward0>))

6. 残差网络(ResNet)

残差网络主要由何凯明等人提出，在2015年ImageNet挑战赛中取得了冠军。

6.1 函数类

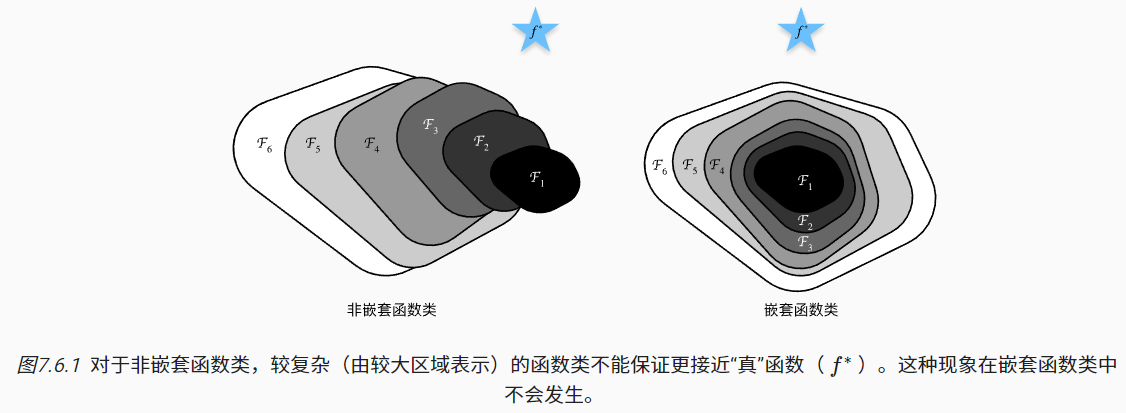
（1）非嵌套函数类

新模型 = 新添加的层 ← 原模型
在先前学习的深度神经网络中，每个神经网络层/块基本独立非嵌套关系，即前者的输出直接作为后者的输入。对于复杂的模型架构，有时新添加的层并不能使模型接近最优解，甚至可能更糟；

（2）嵌套函数类

新模型 = 新添加的层 + 原模型
如果新添加的层效果不明显，新模型仍然有机会基于原模型更新梯度。即新模型可能得出更优的解来拟合数据集（至少不会变差）。

6.2 残差块

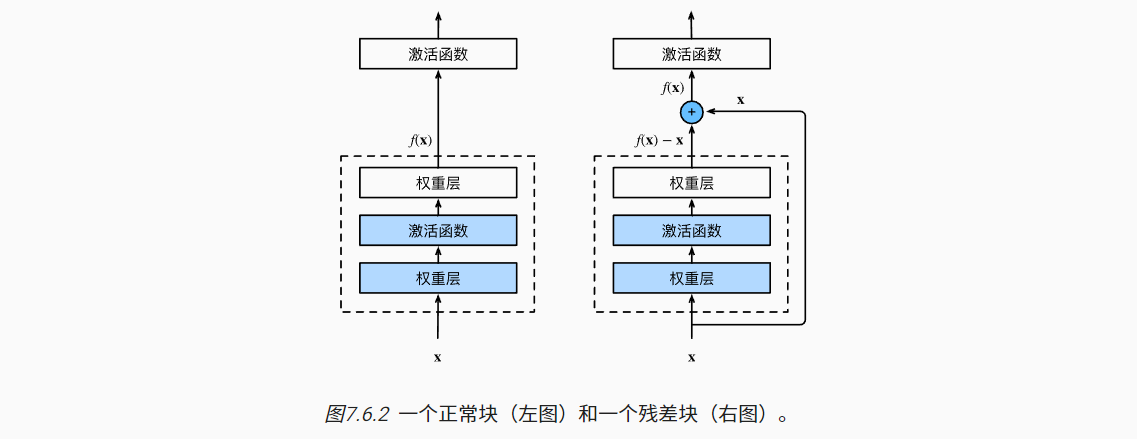
如下左图，为一个正常的神经网络架构，若输出为f(x)。
- 由输入x，经神经网络层映射，得到输出f(x)
如下右图，为一个残差块架构，若输出为f(x)。
- 由输入x，经神经网络层与原数据共同组成f(x)。

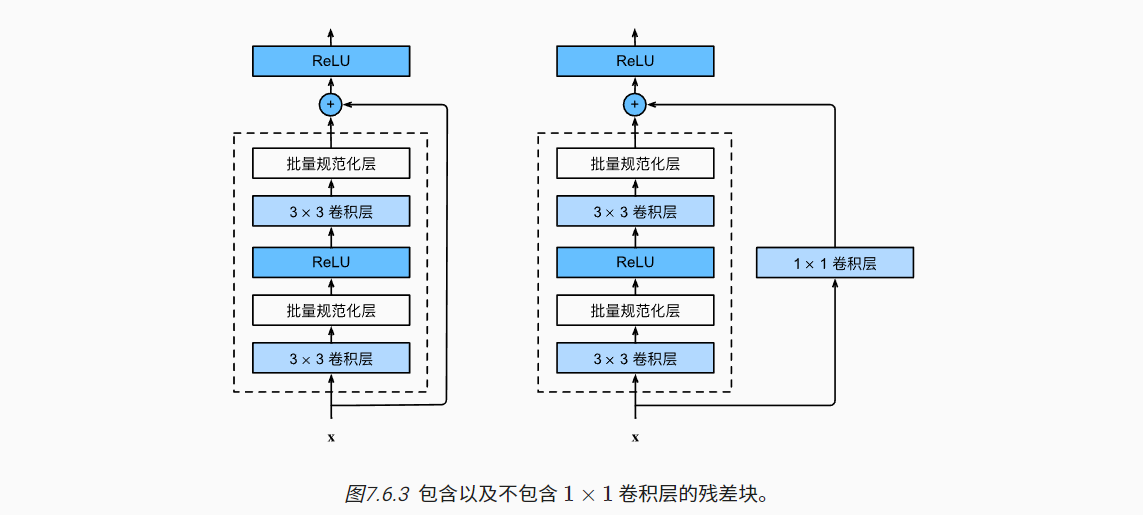
ResNet网络中残差块共有两种，区别在于原模型数据的输入：
- 一种是原模型的x直接输入
- 另一种是原模型的x经1×1卷积层后再输入

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

# input_channels 输入的通道
# num_channels 输出的通道
# use_1x1conv参数声明是否考虑对x进行1×1卷积
# strides 对于第一层卷积以及1×1卷积进行高宽缩减
class Residual(nn.Module):  #@save
    def __init__(self, input_channels, num_channels,
                 use_1x1conv=False, strides=1):
        super().__init__()
        self.conv1 = nn.Conv2d(input_channels, num_channels,
                               kernel_size=3, padding=1, stride=strides)
        self.conv2 = nn.Conv2d(num_channels, num_channels,
                               kernel_size=3, padding=1)
        if use_1x1conv:
            self.conv3 = nn.Conv2d(input_channels, num_channels,
                                   kernel_size=1, stride=strides)
        else:
            self.conv3 = None
        self.bn1 = nn.BatchNorm2d(num_channels)
        self.bn2 = nn.BatchNorm2d(num_channels)

    def forward(self, X):
        Y = F.relu(self.bn1(self.conv1(X)))
        Y = self.bn2(self.conv2(Y))
        if self.conv3:
            X = self.conv3(X)
        Y += X
        return F.relu(Y)

查看示例输出

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


# 输入通道为3，输出通道为3
blk = Residual(3,3) 
X = torch.rand(4, 3, 6, 6) # 4个样本
Y = blk(X)
Y.shape 
# torch.Size([4, 3, 6, 6])

# 输入通道为3，输出通道为6，高宽减半（必须调用1×1卷积）
blk = Residual(3,6, use_1x1conv=True, strides=2)
blk(X).shape
# torch.Size([4, 6, 3, 3])

6.3 ResNet模型

ResNet模型由如下部分组成

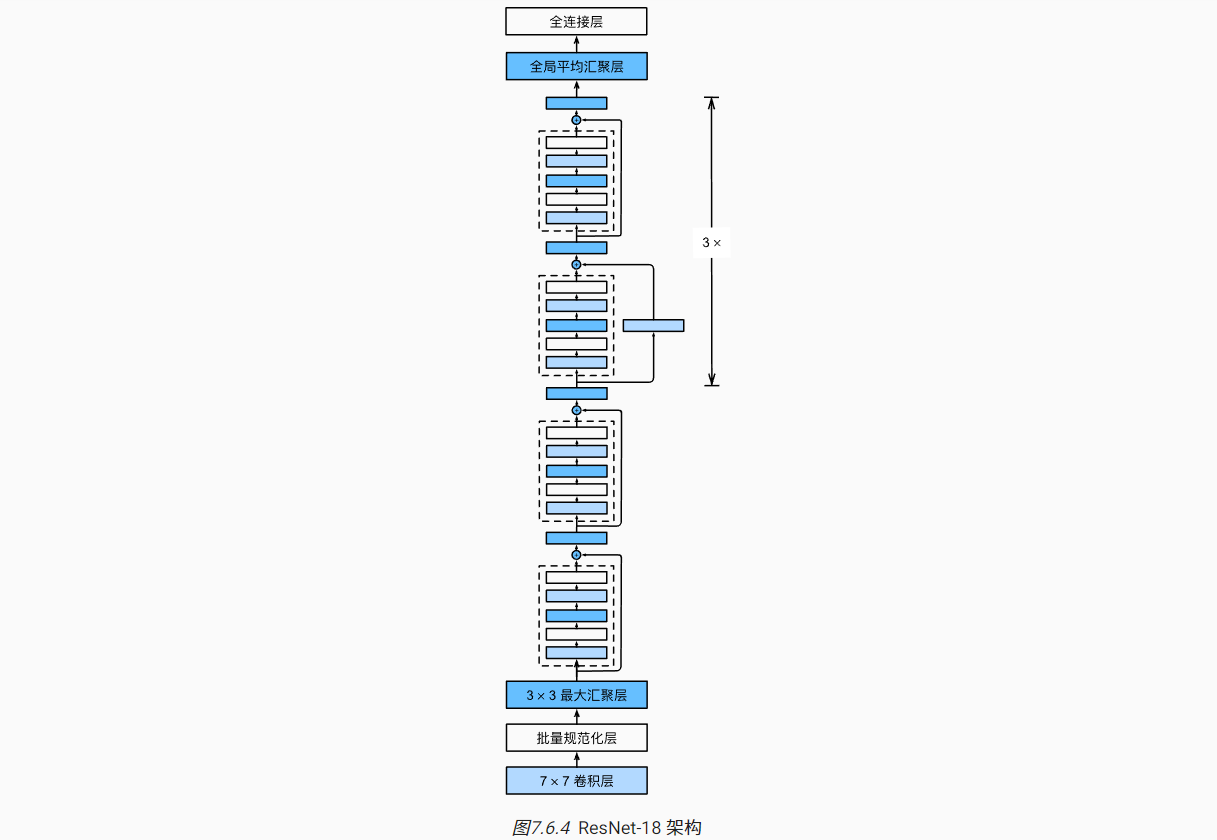
第1部分：卷积层+BN+最大汇聚层，64通道输出，高宽降低四倍

1
2
3


b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
                   nn.BatchNorm2d(64), nn.ReLU(),
                   nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

第2~5部分由4个block组成，每个block包含两个2残差块
- 除了第1个Block以外的第1个残差块都需要将高宽减半，通道数加倍

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


def resnet_block(input_channels, num_channels, num_residuals,
                 first_block=False):
    blk = []
    for i in range(num_residuals):
        if i == 0 and not first_block:
            blk.append(Residual(input_channels, num_channels, #输出通道数是输入的2倍
                                use_1x1conv=True, strides=2))
        else:
            blk.append(Residual(num_channels, num_channels)) #输入输出通道数相同
    return blk

b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))

最后的第6部分连接全局平均汇聚层以及全连接输出层

1
2
3


net = nn.Sequential(b1, b2, b3, b4, b5,
                    nn.AdaptiveAvgPool2d((1,1)),
                    nn.Flatten(), nn.Linear(512, 10))

4个Block包含共包含8个残差块，共16个卷积层，加上第一个卷积层以及最后一个全连接层，共有18层，因此又称为ResNet-18。

查看示例形状输出

1
2
3
4


X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t', X.shape)

6.4 训练模型

1
2
3
4
5
6


lr, num_epochs, batch_size = 0.05, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)

d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
# loss 0.010, train acc 0.998, test acc 0.904
# 10662.5 examples/sec on cuda:0

7. 稠密连接网络(DenseNet)

DenseNet相当于是ResNet的逻辑扩展。

7.1 从ResNet到DenseNet

ResNet和DenseNet的关键区别在于，DenseNet输出是连接（用图中的[,]表示）而不是如ResNet的简单相加。
稠密网络主要由2部分构成：稠密块（dense block）和过渡层（transition layer）。前者定义如何连接输入和输出，而后者则控制通道数量，使其不会太复杂。

7.2 稠密块

基本的“批量规范化、激活和卷积”架构

1
2
3
4
5
6
7
8


import torch
from torch import nn
from d2l import torch as d2l

def conv_block(input_channels, num_channels):
    return nn.Sequential(
        nn.BatchNorm2d(input_channels), nn.ReLU(),
        nn.Conv2d(input_channels, num_channels, kernel_size=3, padding=1)) #高宽不变

一个稠密块由多个卷积块组成，每个卷积块使用相同数量的输出通道；
在前向传播中，我们将每个卷积块的输入和输出在通道维上连结。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


# num_convs 卷积层数, 
# input_channels 输入通道数, 
# num_channels 输出通道数
class DenseBlock(nn.Module):
    def __init__(self, num_convs, input_channels, num_channels):
        super(DenseBlock, self).__init__()
        layer = []
        for i in range(num_convs):
            # 每多一个卷积层，其输入通道数不断增加
            layer.append(conv_block(
                num_channels * i + input_channels, num_channels))
        self.net = nn.Sequential(*layer)

    def forward(self, X):
        for blk in self.net:
            Y = blk(X)
            # 连接通道维度上每个块的输入和输出，即通道数增加
            X = torch.cat((X, Y), dim=1)
        return X

示例展示：第一层输入通道数为3，第二层输入通道数是10+3，第二次输出通道数是10 + 10 + 3

1
2
3
4
5


blk = DenseBlock(2, 3, 10) 
X = torch.randn(4, 3, 8, 8)
Y = blk(X)
Y.shape
# torch.Size([4, 23, 8, 8])

7.3 过渡层

上述稠密层会导致通道数的不断累加、增多
过渡层用来控制模型复杂度，通过1×1卷积层来减小通道数，并使用步幅为2的平均汇聚层减半高和宽。

1
2
3
4
5
6
7
8
9


def transition_block(input_channels, num_channels):
    return nn.Sequential(
        nn.BatchNorm2d(input_channels), nn.ReLU(),
        nn.Conv2d(input_channels, num_channels, kernel_size=1),
        nn.AvgPool2d(kernel_size=2, stride=2))
    
blk = transition_block(23, 10)
blk(Y).shape
# torch.Size([4, 10, 4, 4])

7.4 DenseNet模型

架构基本类似ResNet。

第一部分由单卷积层和最大汇聚层组成

1
2
3
4


b1 = nn.Sequential(
    nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),
    nn.BatchNorm2d(64), nn.ReLU(),
    nn.MaxPool2d(kernel_size=3, stride=2, padding=1))

后面再接4个稠密快，每个块由4个卷积层组成

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


# num_channels为当前的通道数
num_channels, growth_rate = 64, 32
num_convs_in_dense_blocks = [4, 4, 4, 4]
blks = []
for i, num_convs in enumerate(num_convs_in_dense_blocks):
    blks.append(DenseBlock(num_convs, num_channels, growth_rate))
    # 上一个稠密块的输出通道数
    num_channels += num_convs * growth_rate
    # 在稠密块之间添加一个转换层，使通道数量减半
    if i != len(num_convs_in_dense_blocks) - 1:
        blks.append(transition_block(num_channels, num_channels // 2))
        num_channels = num_channels // 2

最后接上全局汇聚层和全连接层来输出结果。

1
2
3
4
5
6


net = nn.Sequential(
    b1, *blks,
    nn.BatchNorm2d(num_channels), nn.ReLU(),
    nn.AdaptiveAvgPool2d((1, 1)),
    nn.Flatten(),
    nn.Linear(num_channels, 10))

7.5 训练模型

1
2
3
4
5
6


lr, num_epochs, batch_size = 0.1, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)

d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())
# loss 0.140, train acc 0.949, test acc 0.887
# 8501.4 examples/sec on cuda:0

1. 深度卷积神经网络(AlexNet)#

1.1 学习表征#

1.2 AlexNet#

1.3 读取数据集#

1.4 训练AlexNet#

2 使用块的网络(VGG)#

2.1 VGG块#

2.2 VGG网络#

2.3 训练模型#

3. 网络中的网络(NiN)#

3.1 NiN块#

3.2 NiN模型#

3.3 训练模型#

4. 含并行连接的网络(GoogLeNet)#

4.1 Inception块#

4.2 GoogLeNet模型#

4.3 训练模型#

5. 批量规范化#

5.1 训练深层网络#

5.2 批量规范化层#

5.3 从零实现#

5.4 使用批量规范化层的LeNet#

6. 残差网络(ResNet)#

6.1 函数类#

6.2 残差块#

6.3 ResNet模型#

6.4 训练模型#

7. 稠密连接网络(DenseNet)#

7.1 从ResNet到DenseNet#

7.2 稠密块#

7.3 过渡层#

7.4 DenseNet模型#

7.5 训练模型#