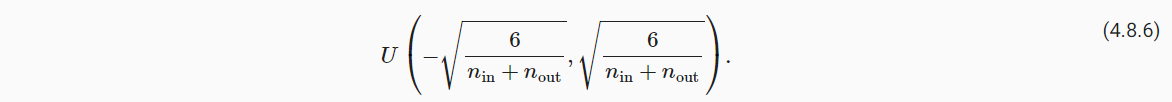1. 多层感知机
1.1 隐藏层
- 之前所学的线性模型意味着单调假设,并不适用于更复杂的建模问题,例如体温与疾病;图片某个像素点的强度与猫或狗的关系等;
- 多层感知机(MLP):在输入层与输出层之间加入一个或多个隐藏层,以学习更加复杂的模型情况;
- 只有隐藏层与输出层涉及到神经元计算与参数更新,因此如下示例MLP的层数是2;
- 对于其中的隐藏层需要应用非线性的激活函数(σ),以突破对仍为线性本质的限制。
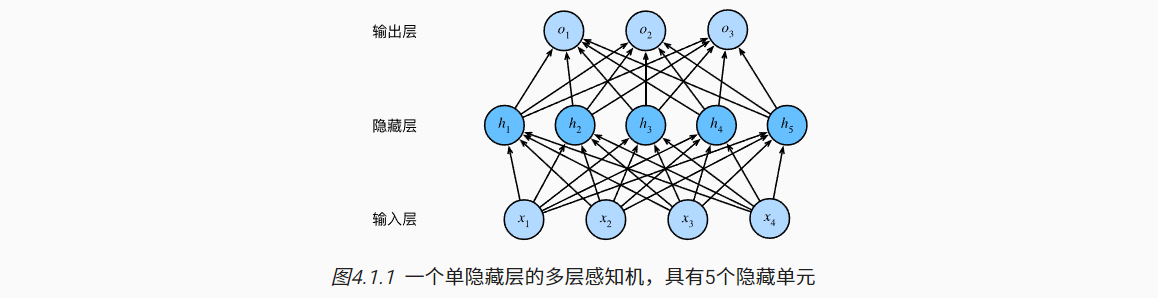
- 对于n个样本,d个特征的输入X (n×d)。中间隐藏层的神经元个数为h,权重参数为W1(d×h),偏置参数为b1(1×h)。输出层神经元个数为q,权重参数为W2(h×q),偏置参数为b2(1×q)。
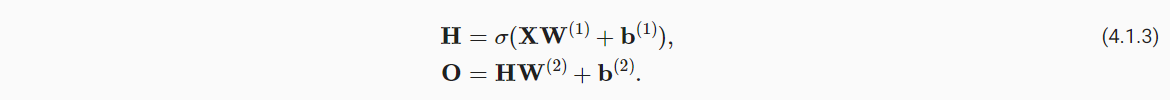
1.2 激活函数
|
|
(1)ReLu函数
- 变换方式:隐藏层输出的结果若为负数,变为0;正数保持不变;
- 实现简单,表现良好。
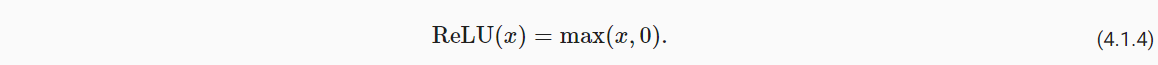
|
|
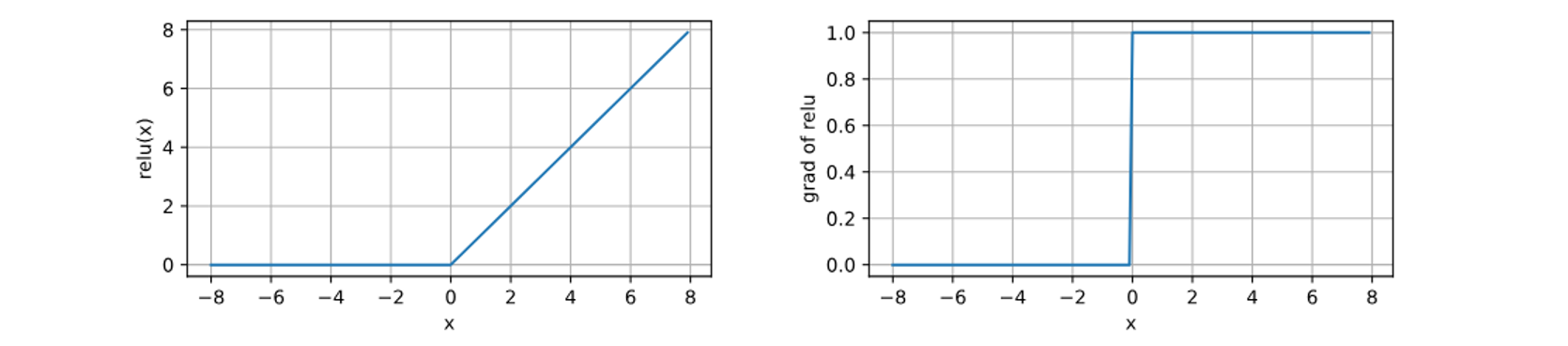
不要太纠结x=0的情况—“如果微妙的边界条件很重要,我们很可能是在研究数学而非工程”
(2)sigmoid函数
- 变换方式:隐藏层输出的结果变换到0与1之间;
- 如今在隐藏层中已经不常用,多用于二分类问题中输出层的激活函数
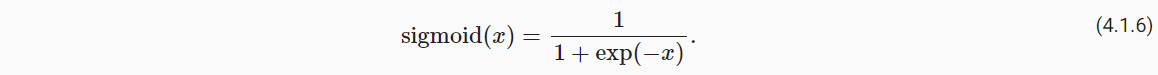
|
|
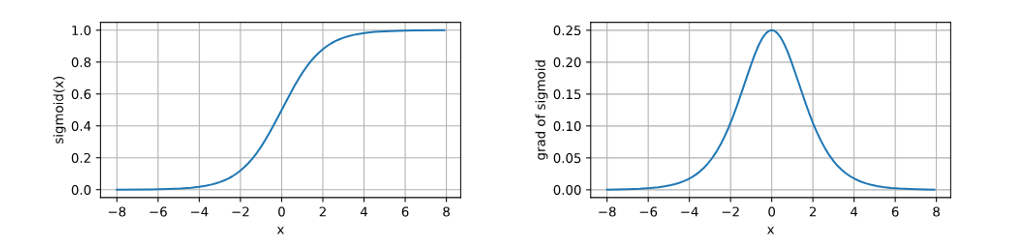
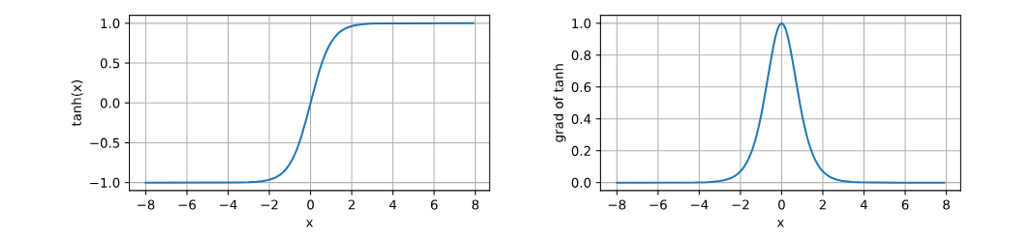
(3)tanh函数(双曲正切)
- 变换方式:隐藏层输出的结果变换到-1与1之间;
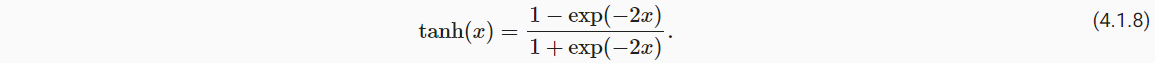
|
|
2. 多层感知机的从零实现
|
|
2.1 初始化模型参数
|
|
2.2 激活函数
- 自定义ReLu函数
|
|
2.3 模型
- 2层MLP结构
|
|
2.4 损失函数
- 交叉熵损失函数
|
|
2.5 训练
- 调用第三章的训练函数
|
|
3. 多层感知机的简洁实现
|
|
|
|
|
|
4. 模型欠拟合和过拟合
4.1 训练误差和泛化误差
- 训练误差:模型在训练数据集上计算得到的误差;
- 泛化误差:模型应用在同样从原始样本的分布中抽取的无限多数据样本时,模型误差的期望(理论);
- 过拟合:模型在训练数据上拟合的比在潜在分布中更接近的现象。
- 影响模型泛化的因素:
- (1)参数数量:可调整参数的数量越多,越容易过拟合;
- (2)参数取值:参数的取值范围越大,越容易过拟合;
- (3)训练样本的数量:原则上,训练样本越少,越容易过拟合。【DL至少要上千样本】
4.2 模型选择
- 比较不同超参数设置下的同一类模型,会涉及到数据集的多种划分方式。
- 方式1:将数据分为3份
- 训练数据集用于训练模型
- 验证数据集用于比较、选择模型
- 测试数据集用于最终的泛化评估(联想高考)
在代码实现部分,教材所写的测试集其实还是验证集。
- 方式2:K折交叉验证(样本量不多时)
- 将数据分为K个子集
- 每次选取K-1个子集训练,在剩余的一个自己验证;
- 取K次实验的均值。
在DL中,由于训练成本较高,不会太常用;在ML中常用。
4.3 欠拟合还是过拟合
- 欠拟合
- 训练误差与验证误差都很大,差距较小;
- 模型可能过于简单,有理由相信可训练更复杂的模型减小训练误差
- 过拟合
- 训练误差明显小于验证误差;
- 值得注意,过拟合并不总是坏事。最终还是更关心验证误差。
4.4 多项式回归
- 教材中举了一个例子直观的解释了模型复杂度(参数数量)对于模型拟合的影响。
- 首先生成了200个样本的20个特征数据;特征分别来自于0~19次幂的结果,而真实的标签y仅来自如下图所示的前四个多项式。
- 第一次训练:取前4列特征,拟合正常;
- 第二次训练:取前2列特征,欠拟合(参数过少);
- 第三次训练:取全部20列数据,过拟合(参数过多)。
- 详见教材代码:https://zh-v2.d2l.ai/chapter_multilayer-perceptrons/underfit-overfit.html
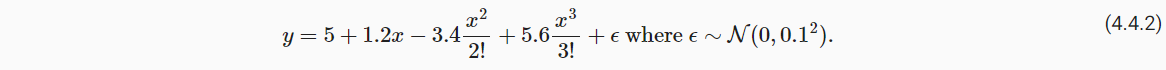
5. 权重衰减
5.1 范数与权重衰减
- 模型复杂度的影响因素之一是参数的大小取值范围,可通过L2范数衡量;
- 可将参数的范数作为惩罚项,和预测损失共同作为最小化的训练目标;
- 如下公式,具体可通过正则化常数λ控制惩罚项的影响程度。
- 较小的λ值对w约束较小;
- 较大的λ值对w约束较大;
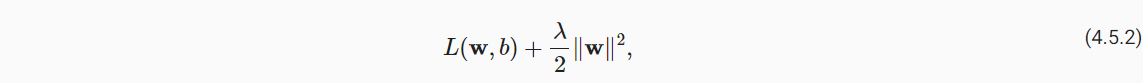
通常,网络输出层的偏置项不会被正则化。
5.2 高维线性回归
- 模拟数据,在5.3演示权重衰减的作用
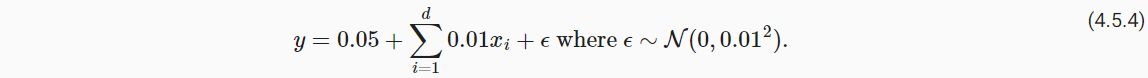
|
|
5.3 从零开始实现
- 初始化模型参数
|
|
- 定义L2范数
|
|
- 定义训练代码实现
|
|
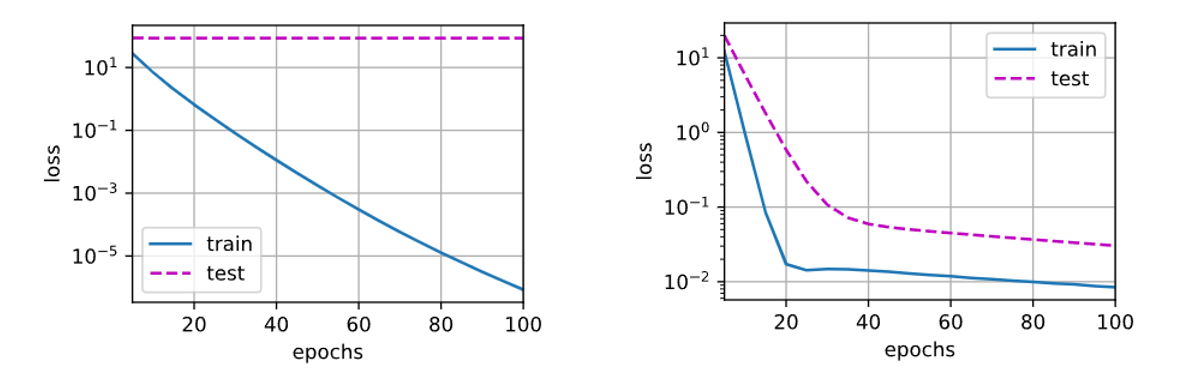
- 训练
|
|
5.4 简洁实现
|
|
|
|
沐神推荐,一般可设置weight_decay为0.01, 0.001, 0.0001
6. 暂退法
6.1 扰动的稳健性
- 防止模型过拟合的另一个角度是增加平滑性,不会对输入的微小变化敏感;
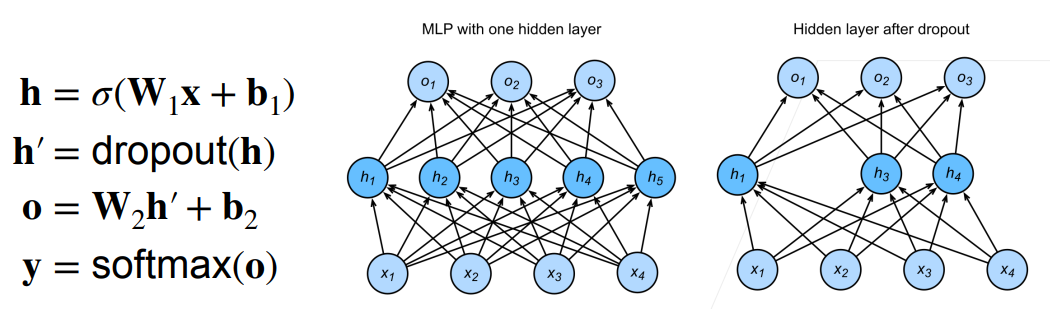
- 暂退法是在前向传播过程中,计算每一内部层的同时引入噪声,表现为随机丢弃(drop out)一些神经元;
- 在标准暂退法正则化中,每个中间隐藏层的激活值h以暂退概率p被随机变量*h’*替换。
上述公式表示按一种无偏向的方式引入噪声,每层的期望值等于没有噪音的值。
6.2 实践中的暂退法
- 暂退法仅用于隐藏层的(激活后)输出结果中,使得不过度依赖隐藏层中的任意一个元素;
- 仅在训练过程中使用Dropout,在预测过程中不需要使用;
- Dropout多应用于MLP神经网络,而较少应用于CNN等
6.3 从零开始实现
- 自定义dropout函数
|
|
- 定义模型
|
|
- 训练测试
|
|
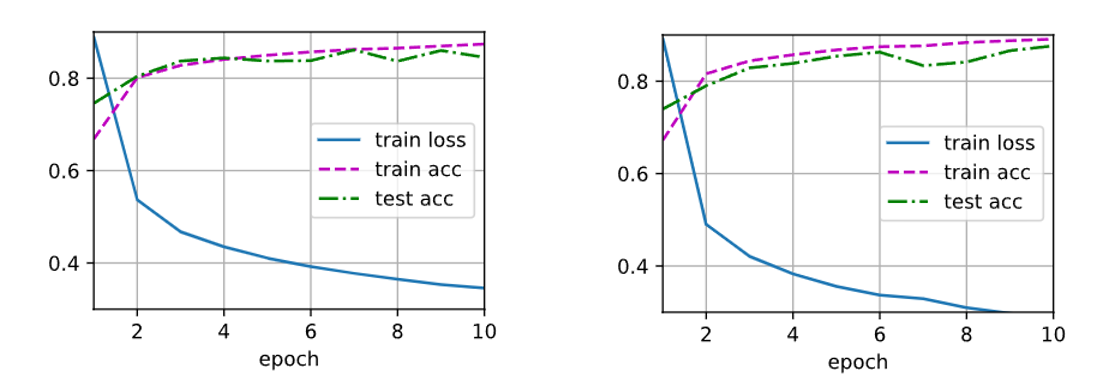
右图:Dropout均设为0的训练结果。
6.4 简洁实现
|
|
7. 前向传播、后向传播和计算图
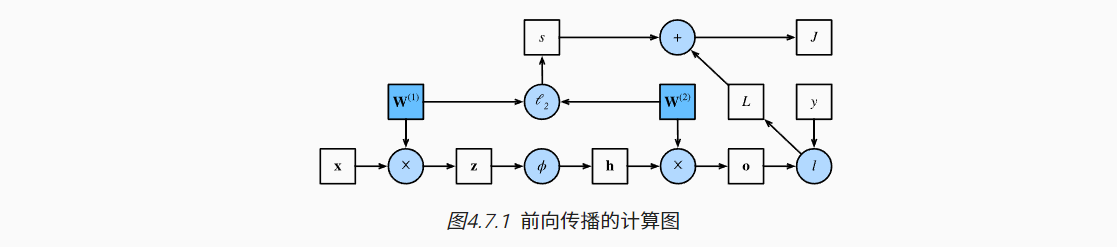
7.1 前向传播
- 前向传播:按顺序(从输入到输出)计算和存储神经网络中每层的结果;
- 如下图举例(简单起见,隐藏层不包括偏置项b)
- 输入层:x
- 隐藏层:参数W(1),输出结果z;激活函数(Φ)输出结果h
- 输出层:参数W(2),输出结果o
- 预测损失:L = l(o, y)
- 惩罚项:s ~ W(1), W(2)
- 目标函数(正则化损失):J = L + s
7.2 反向传播
- 反向传播:从输出层到输入层计算和存储神经网络的参数梯度;
- 如上示例
- 首先计算J分别关于L与s的梯度;
- 然后可计算J关于o的梯度,s关于W(1)、W(2)的梯度;
- 再依次计算J关于W(2)的梯度,J关于h的梯度,J关于z的梯度,J关于W(1)的梯度
7.3 训练神经网络
- 前向传播与反向传播相互依赖;
- 例如
- 前向传播计算的正则化项s取决于模型w1与w2的当前值,由优化算法根据最近迭代的反向传播给出的;
- 反向传播参数的梯度计算,取决于由前向传播给出的隐藏变量h的当前值。
- 反向传播需要重复利用前向传播中储存的中间值,副作用是需要暂用较多的内存。
8. 数值稳定性和模型初始化
8.1 梯度消失与梯度爆炸
- 向量对于向量的梯度为矩阵。当计算目标函数对于特定隐藏层参数的导数可能涉及多个矩阵的乘积。

- 梯度消失:参数更新过小,在每次更新时几乎不会移动,导致模型无法学习
- 一个常见的例子是Sigmoid函数,参考上述2.2部分介绍
- 当Sigmoid函数的输入与输出很大或很小时,梯度近乎消失。
- 梯度爆炸:参数更新过大,破坏了模型的稳定收敛
|
|
8.2 参数初始化
- Xavier初始化:对全连接层权重的初始化取决于输入与输出层的神经元数量
(1)若是正态分布,则从均值为0,方差如下的高斯分布中抽样权重;

(2)也可以改为从下述范围的均匀分布中抽样权重