1. 线性回归

1.1 线性回归的基本元素

  • 线性模型：目标(y)可以表示为输入特征的加权和，参数包括权重向量w和偏置b
  • 损失函数：表示目标的实际值与预测值之间的差距；一般数值越小，损失越小。回归问题常用平方误差函数，如下公式。

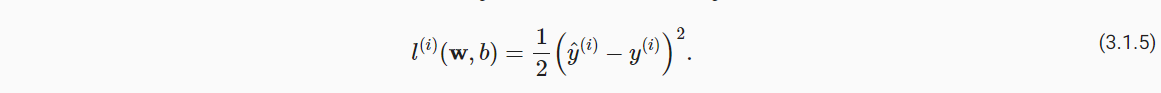
image-20240720171253170

  • 解析解：可以直接计算梯度为0时的参数值。仅对于线性回归类简单问题存在，大部分深度学习问题不存在。

  • 随机梯度下降：不断在损失函数递减的方向上更新参数来降低误差。

    在实际应用中，常采用小批量随机梯度下降。

    1. 即随机抽取少量样本(B)，计算该批量的损失均值关于模型参数的导数；
    2. 然后，将梯度乘以一个预先确定的正数(η，学习率)，并从当前参数的值中减去（梯度负方向上更新参数）。

    这里的B，η为超参数，需要人为指定，不会在训练中更新。模型调参即选择超参数的过程。

  • 用模型预测：基于训练的模型，预测新的样本的结果。

1.2 向量化加速

  • 向量化运算可以显著提高运算时间
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

n = 10000
a = torch.ones(n)
b = torch.ones(n)

#一般操作
c = torch.zeros(n)
for i in range(n):
    c[i] = a[i] + b[i]
    
#向量化操作
d = a + b

1.3 正态分布与平方损失

  • 假设线性回归（的噪声）遵循正态分布，我们可以计算通过给定的x样本观测到特定y标签的似然；
  • 根据极大似然估计法，参数w与b的最优值是使得整个数据集的似然最大的值；
  • 由于损失问题通常是最小化计算，因此需要对计算公式取-log转换；
  • 最后可证明在高斯噪声的假设下，最小化均方误差等价于对线性模型的极大似然估计。

image-20240720174910064

1.4 从线性回归到深度网络

  • 线性回归可以理解为一个单层神经网络；其中每个输入都与每个输出（线性回归只有一个输出）连接。这种变换又称为全连接层，或者稠密层。

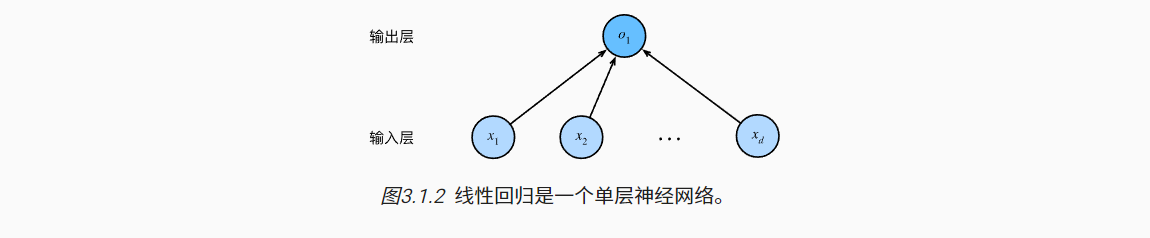
image-20240720175336770

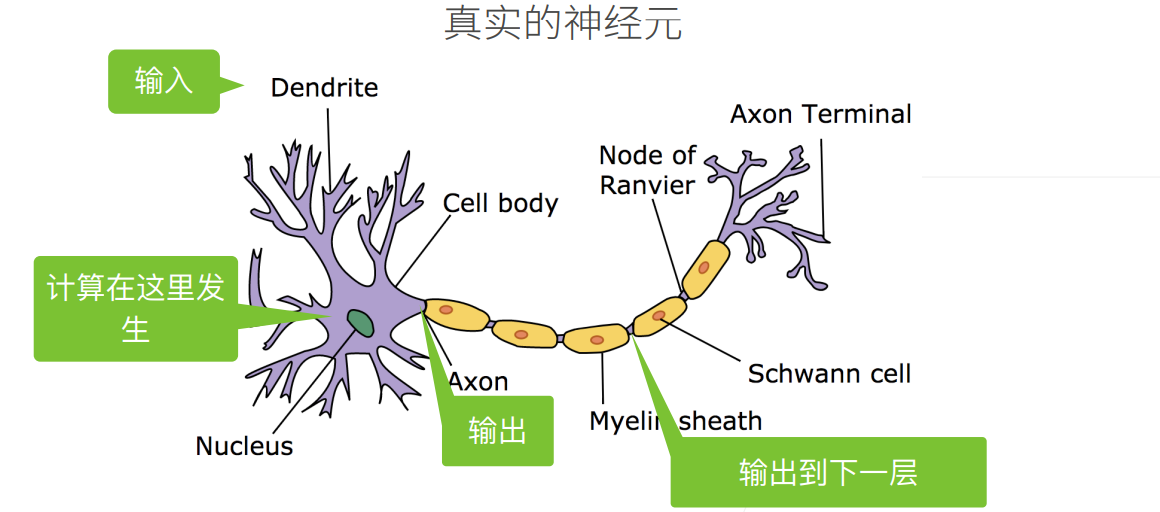
  • 线性回归其实早于神经科学。
image-20240720175457592

2. 线性回归从零实现

2.1 生成数据集

  • 生成一个模拟数据集，两个输入特征，一个输出：y = 2x - 3.4z
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

def synthetic_data(w, b, num_examples):  #@save
    """生成y=Xw+b+噪声"""
    X = torch.normal(0, 1, (num_examples, len(w)))  # (样本数，特征数)矩阵
    y = torch.matmul(X, w) + b		#广播机制
    y += torch.normal(0, 0.01, y.shape)    #随机噪声
    return X, y.reshape((-1, 1))   #y转置为具有1列的矩阵

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = synthetic_data(true_w, true_b, 1000)
features, labels

2.2 小批量读取数据集

  • 小批量数据迭代生成
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

def data_iter(batch_size, features, labels):
    num_examples = len(features)   #总样本数
    indices = list(range(num_examples))
    # 这些样本是随机读取的，没有特定的顺序
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):  #间隔值
        batch_indices = torch.tensor(
            indices[i: min(i + batch_size, num_examples)])  #min操作主要用于最后一个样本（乱序后）
        yield features[batch_indices], labels[batch_indices] #yield专门用于生成样本迭代
        
batch_size = 10
for X, y in data_iter(batch_size, features, labels):
    print(X, '\n', y)
    break

2.3 初始化参数

  • 随机初始化模型的参数
1
2

w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

2.4 定义模型

  • y = Xw + b
1
2
3

def linreg(X, w, b):  #@save
    """线性回归模型"""
    return torch.matmul(X, w) + b

2.5 定义损失函数

  • 对于回归问题，常采用平方误差损失函数；
1
2
3

def squared_loss(y_hat, y):  #@save
    """均方损失"""
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2 #确保y的形状与y_hat一致

2.6 定义优化算法

  • 将模型参数按照梯度的反方向更新；更新大小由学习率η决定。
  • 由于是小批量样本的梯度，需要取均值；使其更新步长不受批量的影响
1
2
3
4
5
6

def sgd(params, lr, batch_size):  #@save
    """小批量随机梯度下降"""
    with torch.no_grad():  #不计算梯度，而是使用梯度结果
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

2.7 训练

  • 每个epoch扫一次全部的样本，涉及多个小批量（取决于Batch大小）；
    • （1）计算小批量的损失
    • （2）计算参数的梯度
    • （3）更新参数
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w, b), y)  # X和y的小批量损失【列向量】
        # 因为l形状是(batch_size,1)，而不是一个标量。l中的所有元素被加到一起，
        # 并以此计算关于[w,b]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():  #每个epoch结束后，返回当前模型的损失
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

3. 线性回归的简洁实现

在Pytorch中，对于数据迭代器、损失函数、优化器和神经网络都有简单、高效的实现方式

3.1 生成数据集

  • 操作步骤同前
1
2
3
4
5
6
7
8

import numpy as np
import torch
from torch.utils import data
from d2l import torch as d2l

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features, labels = d2l.synthetic_data(true_w, true_b, 1000)

3.2 读取数据集

  • 调用Pytorch的数据迭代器
1
2
3
4
5
6
7
8
9

def load_array(data_arrays, batch_size, is_train=True):  #@save
    """构造一个PyTorch数据迭代器"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

batch_size = 10
data_iter = load_array((features, labels), batch_size)

next(iter(data_iter)) #获取、打印一个小批量数据

3.3 定义模型

  • Sequential类可以将多个神经网络层串联在一起；
  • Linear类用于定义全连接层，其中第一个参数指定输入特征形状；第二个参数指定输出特征形状。
1
2
3
4
5

# nn是神经网络的缩写
from torch import nn

net = nn.Sequential(nn.Linear(2, 1))
net

3.4 初始化模型参数

1
2
3
4
5
6

net[0] #第一层
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

net[0].weight.data
net[0].bias.data

3.5 定义损失函数

1

loss = nn.MSELoss()

3.6 定义优化算法

  • SGD小批量随机梯度下降算法，交代模型参数以及学习率
1

trainer = torch.optim.SGD(net.parameters(), lr=0.03)

3.7 训练

  • 逻辑与2.7类似
    • 迭代小批量样本
    • 计算损失
    • 计算梯度
    • 参数更新
1
2
3
4
5
6
7
8
9

num_epochs = 3
for epoch in range(num_epochs):
    for X, y in data_iter:
        l = loss(net(X) ,y) #计算损失
        trainer.zero_grad()		
        l.backward()    #计算梯度
        trainer.step()  #更新参数
    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')

4. softmax回归

4.1 分类问题

  • 独热编码用于表示分类数据；
  • 其本质为一个向量，元素分量与类别数一样多；
  • 对于某个具体样本，真实类别对应的分量为1，其它分量为0。

4.2 网络架构

  • 具有多个输出的单层神经网络模型，以分别估计每个类别的概率；
  • 基于全连接层的特性，所有输入特征都与每个输出建立关系；

image-20240720205606452

4.3 全连接层的参数开销

  • 若具有d个（特征）输入，q的输出（类别）的全连接层，则参数开销为O(dq)

4.4 softmax运算

  • 将模型输出结果视为概率的前提是（1）非负，（2）和为1；
  • Softmax操作可以将输出进行转换，满足上述条件。（1）首先将输出结果求幂（2）每个求幂的结果除以结果的总和；

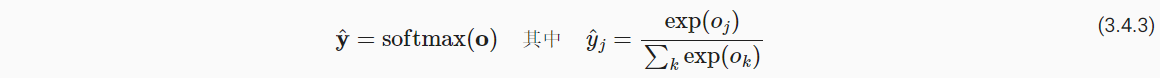
image-20240720210957383

虽然softmax是一个非线性函数，但softmax回归的输出还是由输出特征的全连接层得到的，因此softmax回归是线性模型

4.5 小批量样本的向量化

对于具有n个样本，特征维度为d，类别数为q的小批量数据：

  • 特征矩阵X： n × d
  • 权重W：d × q
  • 偏置b：1 × q
  • 输出结果O：n × q

4.6 损失函数

  • 多分类问题常使用交叉熵作为损失函数，其只关心（最大化）对于正确类别预测的预测概率；

image-20240720215934769

此外，也可从信息论的角度理解交叉熵损失，详见教材3.4.7小结

5 图像分类数据集

  • Fashion-MNIST数据集：10个类别图像组成；6000个训练样本，1000个测试样本
1
2
3
4
5
6
7
8

%matplotlib inline
import torch
import torchvision
from torch.utils import data
from torchvision import transforms
from d2l import torch as d2l

d2l.use_svg_display()

5.1 读取数据集

  • 下载到本地上一级的data目录下
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

# 通过ToTensor实例将图像数据从PIL类型变换成32位浮点数格式，
# 并除以255使得所有像素的数值均在0～1之间
trans = transforms.ToTensor()
mnist_train = torchvision.datasets.FashionMNIST(
    root="../data", train=True, transform=trans, download=True)
mnist_test = torchvision.datasets.FashionMNIST(
    root="../data", train=False, transform=trans, download=True)

len(mnist_train) #6000
len(mnist_train[0]) #2,长度为2的tuple
mnist_train[0][0].shape #特征形状 [1, 28, 28]
mnist_train[0][1]       #样本类别

5.2 读取小批量

  • 参考3.2，使用Pytorch的Dataloader类
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

batch_size = 256

def get_dataloader_workers():  #@save
    """使用4个进程来读取数据"""
    return 4

train_iter = data.DataLoader(mnist_train, batch_size, shuffle=True,
                             num_workers=get_dataloader_workers())

next(iter(train_iter))

5.3 整合所有组件

  • 合并上述操作于一个函数
  • resize参数表示调整，修改图片的形状
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

def load_data_fashion_mnist(batch_size, resize=None):  #@save
    """下载Fashion-MNIST数据集，然后将其加载到内存中"""
    trans = [transforms.ToTensor()]
    if resize:
        trans.insert(0, transforms.Resize(resize))
    trans = transforms.Compose(trans)
    mnist_train = torchvision.datasets.FashionMNIST(
        root="../data", train=True, transform=trans, download=True)
    mnist_test = torchvision.datasets.FashionMNIST(
        root="../data", train=False, transform=trans, download=True)
    return (data.DataLoader(mnist_train, batch_size, shuffle=True,
                            num_workers=get_dataloader_workers()),
            data.DataLoader(mnist_test, batch_size, shuffle=False,
                            num_workers=get_dataloader_workers()))

    
train_iter, test_iter = load_data_fashion_mnist(32, resize=64)
for X, y in train_iter:
    print(X.shape, X.dtype, y.shape, y.dtype)
    break

6 softmax回归的从零开始实现

  • 设置数据迭代器的批量大小为256
1
2
3
4
5
6

import torch
from IPython import display
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

6.1 初始化模型参数

  • 这里将每个样本视为长度为784的向量
1
2
3
4
5

num_inputs = 784  # 1 * 28 * 28
num_outputs = 10

W = torch.normal(0, 0.01, size=(num_inputs, num_outputs), requires_grad=True)
b = torch.zeros(num_outputs, requires_grad=True)

6.2 定义Softmax操作

  • （1）非负；（2）和为1
1
2
3
4
5
6
7
8

def softmax(X):
    X_exp = torch.exp(X) # 求幂
    partition = X_exp.sum(1, keepdim=True) #得到了列向量，表示每一行的和
    return X_exp / partition  # 这里应用了广播机制

X = torch.normal(0, 1, (2, 5))
X_prob = softmax(X)
X_prob, X_prob.sum(1)

6.3 定义模型

  • 先计算原始计算结果；在进行softmax转换
1
2
3
4

X.reshape((-1, W.shape[0])).shape # [256, 784]

def net(X):
    return softmax(torch.matmul(X.reshape((-1, W.shape[0])), W) + b)

6.4 定义损失函数

  • 参考4.6步骤，交叉熵损失函数主要计算模型对于真实标签类别的负对数似然
1
2
3
4
5
6
7
8

# 表示真实类别的预测概率
y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y_hat[[0, 1], y]

def cross_entropy(y_hat, y):
    return - torch.log(y_hat[range(len(y_hat)), y])
cross_entropy(y_hat, y)

6.5 分类精度

  • 通常取预测概率最高的类别作为预测结果；
  • 分类精度是正确预测数与预测总数之比。
1
2
3
4
5
6
7
8

def accuracy(y_hat, y):  #@save
    """计算预测正确的数量"""
    if len(y_hat.shape) > 1 and y_hat.shape[1] > 1:
        y_hat = y_hat.argmax(axis=1)  #沿轴1，最大值元素所对应的位置
    cmp = y_hat.type(y.dtype) == y  #逻辑值
    return float(cmp.type(y.dtype).sum()) #求和

accuracy(y_hat, y) / len(y)
  • 对于数据迭代器，评估其在全部数据集的精度
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

def evaluate_accuracy(net, data_iter):  #@save
    """计算在指定数据集上模型的精度"""
    if isinstance(net, torch.nn.Module):
        net.eval()  # 将模型设置为评估模式
    metric = Accumulator(2)  # 正确预测数、预测总数
    with torch.no_grad():
        for X, y in data_iter:  #每次迭代一次小批量，分别累加正确预测数、预测总数
            metric.add(accuracy(net(X), y), y.numel())
    return metric[0] / metric[1]

class Accumulator:  #@save
    """在n个变量上累加"""
    def __init__(self, n):
        self.data = [0.0] * n

    def add(self, *args):
        self.data = [a + float(b) for a, b in zip(self.data, args)]

    def reset(self):
        self.data = [0.0] * len(self.data)

    def __getitem__(self, idx):
        return self.data[idx]

6.6 训练

  • 定义一个函数训练一轮
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

def train_epoch_ch3(net, train_iter, loss, updater):  #@save
    """训练模型一个迭代周期（定义见第3章）"""
    # 将模型设置为训练模式
    if isinstance(net, torch.nn.Module):
        net.train()
    # 训练损失总和、训练准确度总和、样本数
    metric = Accumulator(3)
    for X, y in train_iter:
        # 计算梯度并更新参数
        y_hat = net(X)
        l = loss(y_hat, y)
        if isinstance(updater, torch.optim.Optimizer):
            # 使用PyTorch内置的优化器和损失函数
            updater.zero_grad()
            l.mean().backward()
            updater.step()
        else:
            # 使用定制的优化器和损失函数
            l.sum().backward()
            updater(X.shape[0])
        metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
    # 返回训练损失和训练精度
    return metric[0] / metric[2], metric[1] / metric[2]
  • 定义一个训练函数，会运行多个epoch。每个epoch训练完，会评估在test测试数据的效果
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):  #@save
    """训练模型（定义见第3章）"""
    animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                        legend=['train loss', 'train acc', 'test acc'])
    for epoch in range(num_epochs):
        train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
        test_acc = evaluate_accuracy(net, test_iter)
        animator.add(epoch + 1, train_metrics + (test_acc,))
    train_loss, train_acc = train_metrics
    assert train_loss < 0.5, train_loss
    assert train_acc <= 1 and train_acc > 0.7, train_acc
    assert test_acc <= 1 and test_acc > 0.7, test_acc
  • 优化函数
1
2
3
4

lr = 0.1

def updater(batch_size):
    return d2l.sgd([W, b], lr, batch_size)
  • 开始训练
1
2

num_epochs = 10
train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater)

7. softmax回归的简洁实现

  • 设置数据迭代器的批量大小为256
1
2
3
4
5
6

import torch
from IPython import display
from d2l import torch as d2l

batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

7.1 初始化模型参数

1
2
3
4
5
6
7
8
9

# PyTorch不会隐式地调整输入的形状。因此，
# 我们在线性层前定义了展平层（flatten），来调整网络输入的形状
net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

7.2 损失函数

1

loss = nn.CrossEntropyLoss(reduction='none')

7.3 优化算法

1

trainer = torch.optim.SGD(net.parameters(), lr=0.1)

7.4 训练

1
2

num_epochs = 10
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)