1. 数据操作

1.1 入门

  • 张量：具有多个维度（轴）的数组。

    具有一个轴的张量，对应数学上的向量；

    具有两个轴的张量，对应数学上的矩阵。

  • 创建张量

1
2
3
4
5
6
7
8
9

import torch

x = torch.arange(12) # 长度为12个行向量

torch.zeros((2, 3, 4))
torch.ones((2, 3, 4))
torch.randn(3, 4)

torch.tensor([[2,1,4,3],[1,2,3,4],[4,3,2,1]])
  • 基本信息
1
2
3
4
5

x.shape
x.numel #元素个数
X = x.reshape(3, 4) #修改形状
x.reshape(-1, 4)
x.reshape(3, -1)

1.2 运算符

  • 任意两个形状相同的张量，执行基本运算符时，均为按元素操作，结果的形状不变。
1
2
3
4

x = torch.tensor([1.0, 2, 3, 4])
y = torch.tensor([2, 2, 2, 2])

x-y, x+y, x*x, x/y, x**y
  • 张量连接操作concatenate
1
2
3
4
5

x = torch.arange(12, dtype = torch.float32).reshape(3, 4)
y = torch.tensor([[2,1,4,3],[1,2,3,4],[4,3,2,1]])

torch.cat((x, y), dim = 0) #纵向拼接，增加轴0的维度/行
torch.cat((x, y), dim = 1) #横向拼接，增加轴1的维度/列
  • 逻辑运算符构建逻辑张量
1

x == y

1.3 广播机制

  • 形状不同的两个张量执行基本运算时，会适当复制元素扩展数组，使二者具有相同形状，再按元素计算
1
2
3
4
5
6

x = torch.arange(6)
x + torch.tensor(1)

a = torch.arange(3).reshape(3, 1)
b = torch.arange(2).reshape(1, 2)
a + b

1.4 索引切片

  • 类似Python数组操作
1
2
3
4

X = torch.arange(12).reshape(3, 4)
X[-1]  #最后一行
X[1:3] #第二、三行
X[:, 1:3] #第二、三列

1.5 节省内存

  • 变量名赋值新的计算结果时，会重新分配内存
1
2
3
4
5
6

a = torch.tensor(0)
before = id(a) #内存地址

a = a + torch.tensor(1) # 重新分配内存
id(a) == before
# False
  • 原地更新、覆盖先前的计算结果
1
2
3
4
5

a = torch.tensor(0)
before = id(a) #内存地址

a[:] = a + torch.tensor(1)
id(a) == before

1.6 转为其它Python对象

  • 转为Numpy数组
1
2
3

A = X.numpy() # tensor→numpy

torch.tensor(A) # numpy→tensor
  • 大小为1的张量转为Python标量
1
2
3
4
5

a = torch.tensor(3.0)

a.item()
float(a)
int(a)

2. 数据预处理

2.1 读取数据集

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

import os
import pandas as pd

os.makedirs(os.path.join('..','data'), exist_ok=True) #上一级目录创建data文件夹
data_file = os.path.join('..', 'data', 'house_tiny.csv')
with open(data_file, 'w') as f:
    f.write('NumRooms,Alley,Price\n') #列名
    f.write('NA,Pave,127500\n') #每行一个样本
    f.write('2,NA,106000\n')
    f.write('4,NA,178100\n')
    f.write('NA,NA,140000\n')    
    
data = pd.read_csv(data_file)
data

2.2 处理缺失值

1
2
3
4
5
6
7
8
9

inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2] #按列拆分为两个表

# 数值缺失值填充
inputs = inputs.fillna(inputs.mean(numeric_only=True))
inputs

# 类别缺失值填充
inputs = pd.get_dummies(inputs, dummy_na=True, dtype = float)
inputs

2.3 转换为张量

1
2
3
4

import torch
X, y = torch.tensor(inputs.values), torch.tensor(outputs.values)
X, y
# 深度学习通常用float32

3. 线性代数

3.1 标量

  • 只有一个元素的张量
  • 普通、小写的字母表示
1
2
3
4
5
6

import torch

x = torch.tensor(3.0)
y = torch.tensor(4.0)

x + y, x - y, x / y, x ** y

3.2 向量

  • 具有一个轴的张量
  • 粗体、小写的字母表示
1
2
3

x = torch.arange(4)
x
x.shape

向量/轴的维度表示向量或轴的长度；

张量的维度表示张量具有的轴数。

3.3 矩阵

  • 具有两个轴的张量
  • 粗体、大写的字母表示
1
2
3
4
5
6
7

A = torch.arange(20).reshape(5, 4)
A.shape

B = A.T  #转置矩阵

## 对称矩阵，转置后等于转置前
A == A.T

3.4 张量

  • 具有任意数量轴的n维数组
1
2

X = torch.arange(24).reshape(2, 3, 4)
X.shape

3.5 张量算法的基本性质

  • 张量与一个标量的基本运算不会改变张量的形状；
  • 相同形状的两个张量运算（按元素）结果仍是相同形状的张量
1
2
3
4
5
6
7
8

a = 2
X = torch.arange(24).reshape(2, 3, 4)
X + a

A = torch.arange(20, dtype = float32).reshape(5, 4)
B = A.clone()   #分配新内存，隔离
A, A + B
A * B      #哈达玛积

3.6 降维

  • 默认调用求和函数会计算张量所有元素的和，返回一个标量
1
2

x = torch.arange(4, dtype = float32)
x.sum()
  • 指定轴进行求和，会消除该轴，得到降维结果
1
2
3

A = torch.arange(20, dtype = float32).reshape(5, 4)
A.sum(axis = 0)
A.sum(axis = 1)

.mean()求平均值，操作与上述类似。

  • 非降维求和，方便应用广播机制（前提是张量的轴数相同）
1

A.sum(axis = 0, keepdims = True)

3.7 点积

  • 两个向量按相同位置乘积的和
1
2
3
4
5

x = torch.arange(4, dtype = float32)
y = torch.ones(4, dtype = float32)
torch.dot(x, y)
# 等价于
torch.sum(x * y)

3.8 矩阵—向量积

  • 矩阵的列数（轴0的维度）等于向量的长度；
  • 矩阵的每一行与向量的点积；
  • 最大的用途：将向量的维度改变
1
2
3
4

A = torch.arange(20, dtype = float32).reshape(5, 4)
x = torch.arange(4, dtype = float32)

torch.mv(A, x) # length 5

3.9 矩阵乘法

  • 左边矩阵的列数等于右边矩阵的行数
  • 可以理解为右边矩阵的每一行与左边矩阵的计算结果，再拼接为矩阵
1
2
3
4

A = torch.arange(20, dtype = float32).reshape(5, 4)
B = torch.ones(4, 3)

torch.mm(A, B)  #(5, 3)

3.10 范数

  • 范数可以理解为距离大小的度量
  • 向量的L2范数：向量元素平方和的平方根
1
2

u = torch.tensor([3.0, 4.0])
torch.nom(u)
  • 向量的L1范数：向量元素的绝对值之和
1

torch.abs(u).sum()
  • 矩阵的F范数：矩阵元素平方和的平方根
1

torch.norm(torch.ones(4, 9))

4. 微积分

4.1 导数和微分

  • 微分是一种表达方式，表示当自变量有一个微小变化时，因变量的近似变化。
  • 导数是一个数值，其计算为：对于包含模型参数的损失函数，如果将参数增加或减少一个无穷小的量，损失会以多快的速度增加或减少
  • 导数的几何理解：曲线在特点处的切线的斜率

image-20240720110240386

4.2 偏导数

  • 上述导数计算的(损失)函数中，只有一个自变量（参数）；
  • 当函数有多个变量时，分别对每一个自变量（参数）的导数，称为偏导数；

image-20240720110455427

4.3 梯度

  • 标量y对于向量x（多个自变量）的求导结果是向量；
  • 梯度向量表示一个多元函数对于其每个变量的偏导数，综合指向梯度下降最快的方向。

image-20240720112132156

4.4 链式法则

  • 上述的方法方便理解，但难以计算梯度；
  • 对于复合函数，可应用链式法则求微分；

image-20240720112854141

  • 例如两层MLP神经网络。第一层有n个神经元（x1，x2…）；第二层有m个神经元（u1，u2，…），输出层为y。而y对于第一层中任意一个偏导数可以表示为：

image-20240720112834173

5. 自动微分

5.1 简单例子

  • 深度学习会根据模型框架，构建一个计算图，跟踪哪些数据通过那些操作组合起来产生输出；
  • 然后从输出项开始，通过反向传播梯度，计算关于每个参数的偏导数；
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

import torch

x = torch.arange(4.0)
# 声明需要储存梯度
x.requires_grad_(True)
# 查看梯度，默认值为None
x.grad

#给定一个函数
y = 2 * torch.dot(x, x)  # y = 2[(x1)2 + (x2)2 + (x3)2 + (x4)2]
y.backward  #反向传播每个参数的偏导数
x.grad      #梯度计算结果
  • 计算另一个函数的梯度时，需要清楚之前的值
1
2
3
4

x.grad.zero_()
y = x.sum()  # y = x1 + x2 + x3 + x4
y.backward()
x.grad

5.2 非标量的反向传播

  • 标量y对于向量x的导数是一个向量
  • 向量y对于向量x的导数是一个矩阵
  • 在深度学习应用场景中，多见于小批量样本训练。实现形式并非计算微分矩阵，而是单独计算批量中每个样本的偏导数之和。
1
2
3
4

x.grad.zero_()
y = x * x          # 向量
y.sum().backward()
x.grad

5.3 分离计算

  • y = f(x)

  • z = f(y, x)

  • 计算z关于x的梯度。但由于某种原因，希望将y视为一个常数，只考虑x在y被计算后的作用。

1
2
3
4
5
6
7

x.grad.zero_()
y = x * x
u = y.detach()  #视为常数
z = u * x       #x的导数为1

z.sum().backward()
x.grad() == u

6. 概率

6.1 联合概率

  • P(A, B)：表示事件A，B同时发生的概率
  • P(A, B) ≤ P(A)：事件A，B同时发生的概率小于等于事件A或B单独发生的概率

6.2 条件概率

  • P(B|A)：表示在事件A发生前提下，B发生的概率
  • P(B|A) = P(A, B) / P(A)

6.3 贝叶斯定理

  • 由条件概率可得：P(A, B) = P(B|A)*P(A)
  • 根据对称性可得：P(A, B) = P(A|B)*P(B)
  • 所以可推导： P(A|B) = P(B|A)*P(A) / P(B)
    • P(A) 称为先验概率
    • P(A|B)称为后验概率
    • P(B|A)称为似然
    • P(B)称为全概率

6.4 边际化

  • 事件B的概率相当于计算A的所有可能选择，并将所有选择的联合概率聚合在一起。

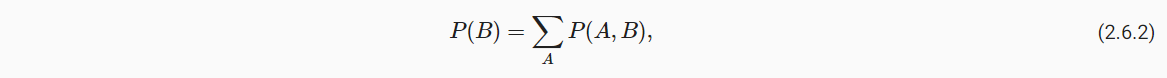
image-20240721200657400

6.5 独立性

  • 若事件A与B是独立的，意味着A的发生与B的发生无关
  • P(B|A) = P(A, B) / P(A) = P(B) 进一步可得 P(A, B) = P(A) * P(B)