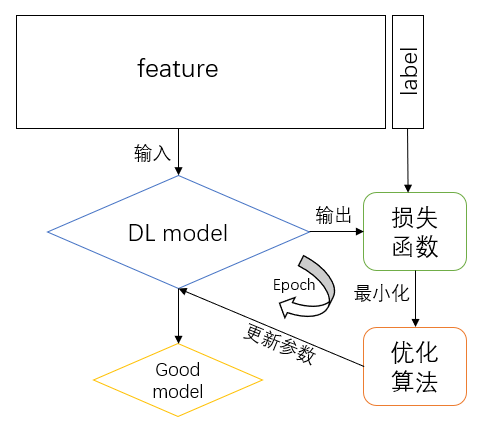
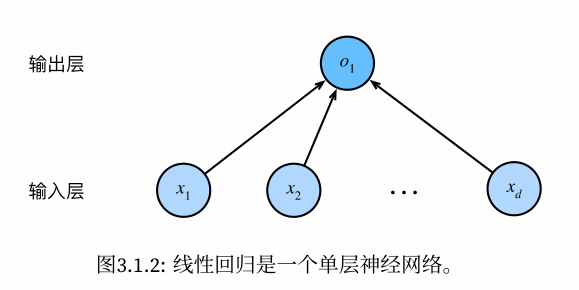
1
2
3

import numpy as np
import torch
import random

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

#模拟生成含有n个特征的线性回归数据
def synthetic_data(w, b, num_examples):
	X = torch.normal(0, 1, (num_examples, len(w)))
	y = torch.matmul(X, w) + b  
	y += torch.normal(0, 0.01, y.shape)
	return X, y.reshape((-1, 1))  

def data_iter(batch_size, features, labels):
	num_examples = len(features)
	indices = list(range(num_examples))
	random.shuffle(indices)
	for i in range(0, num_examples, batch_size):
		batch_indices = torch.tensor(
			indices[i:min(i+batch_size, num_examples)])
		yield features[batch_indices], labels[batch_indices]

# true_w = torch.tensor([2.5, -6.2])
# true_b = 1.2
# features, labels = synthetic_data(true_w, true_b, 10)
# next(iter(data_iter(2, features, labels)))
# # (tensor([[-0.0439, -0.0902],
# #          [ 1.2628,  1.4977]]),
# #  tensor([[ 1.6495],
# #          [-4.9359]]))

1
2
3
4
5

def linreg(X, w, b):
	return torch.matmul(X, w) + b
#初始化模型参数
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

1
2

def squard_loss(y_hat, y):
	return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

1
2
3
4
5

def sgd(params, lr, batch_size):
	with torch.no_grad():
		for param in  params:
			param -= lr * param.grad / batch_size
			param.grad.zero_()

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

true_w = torch.tensor([2.5, -6.2])
true_b = 1.2
features, labels = synthetic_data(true_w, true_b, 100)
batch_size = 10
lr = 0.01 
net = linreg
loss = squard_loss
num_epochs = 30

for epoch in range(num_epochs):
	for X, y in data_iter(batch_size, features, labels):
		l = loss(net(X, w, b), y)
		l.sum().backward()
		sgd([w, b], lr, batch_size)
	with torch.no_grad():
		train_l = loss(net(features, w, b), labels)
		print(f'epoch {epoch + 1}, loss {train_l.mean():f}')

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

## 2.1 示例数据
def synthetic_data(w, b, num_examples):
	X = torch.normal(0, 1, (num_examples, len(w)))
	y = torch.matmul(X, w) + b  
	y += torch.normal(0, 0.01, y.shape)
	return X, y.reshape((-1, 1))  

## 小批量传入样本特征与标签数据
def load_array(data_arrays, batch_size, is_train=True):
	# 类似zip，将两个具有相同行数的数据对应关联在一起
	dataset = data.TensorDataset(*data_arrays)
	# dataset[0:3]
	return data.DataLoader(dataset, batch_size, shuffle=is_train)


## 2.2 定义模型
net = nn.Sequential(nn.Linear(2, 1))

## 2.3 定义损失函数
loss = nn.MSELoss()

## 2.4 定义优化算法
optimizer = torch.optim.SGD(net.parameters(), lr=0.01)

## 2.5 训练模型
true_w = torch.tensor([2.5, -6.2])
true_b = 1.2
features, labels = synthetic_data(true_w, true_b, 50)
batch_size = 5
data_iter = load_array((features, labels), batch_size)
# next(iter(data_iter))

num_epochs = 100
for epoch in range(num_epochs):
	for X, y in data_iter: 
		l = loss(net(X), y)
		optimizer.zero_grad()
		l.backward()
		optimizer.step()
	l = loss(net(features), labels)
	print(f'epoch {epoch + 1}, loss {l:f}')