1、算法与工具简介#
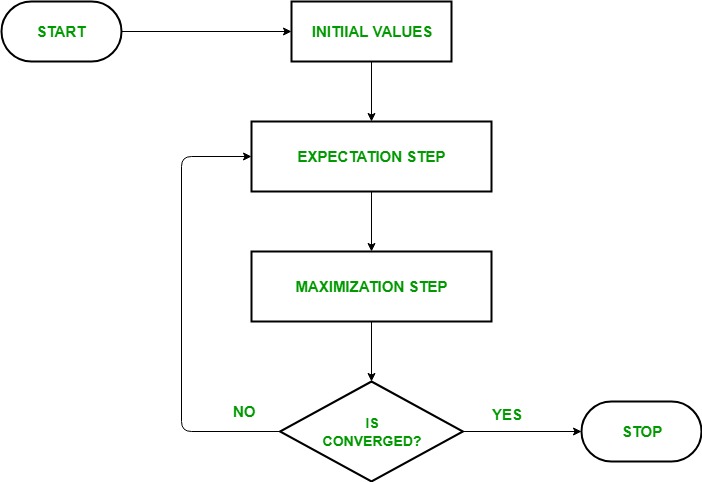
1.1 EM算法#
EM, Expectation-Maximization 期望最大化算法
混合分布:来自两种或两种以上概率分布(高斯分布最典型)的随机数据组成的一组混合数据所形成的分布。
混合模型聚类:识别混合分布中,样本的原始分布,从而进行聚类(一种原始分布对应一个聚类),属于软聚类。
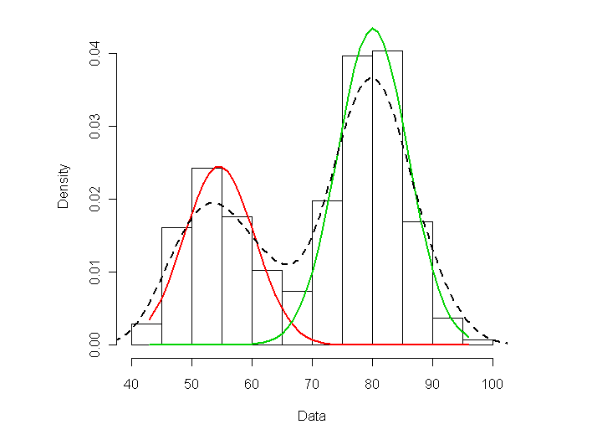
假设一组混合分布的30个数据,虚线为混合分布的概率密度。混合模型聚类的目的就是找到其中哪些样本属于红色分布类,哪些样本属于绿色分布类。
(已知:其中10个来自红色正态分布,20个来自绿色正态分布。在计算时是不知道这一信息)
后验概率(posterior probability):样本属于某种特定分布的概率
似然概率(likelihood probability):在某种特定分布中观察到样本的概率
先验概率(prior probability):在混合样本中,属于某种特定分布的样本数目
全概率:在混合样本中的概率密度
根据贝叶斯公式
$$
后验概率 = \frac{似然概率×先验概率}{全概率}
$$
- 某一样本的全概率等于:红色正态分布中出现该样本的概率加上绿色正态分布中出现该样本的概率。
$$
x_i = p(x_i|k_红)×p(k_红) + p(x_i|k_绿)×p(k_绿)
$$
$$
p(k_{红}|x_i) = \frac{p(x_i|k_红)×p(k_红)}{x_i}
$$
$$
p(k_{绿}|x_i) = \frac{p(x_i|k_绿)×p(k_绿)}{x_i}
$$
(1)首先假定混合分布中样本来自几种原始正态分布,这里假设为2。
(2)初始化每种正态分布的特征参数(均值、方差)与先验概率(属于两种分布的样本比例)。
(3)根据每种分布当前的特征参数,计算两种分布对于每个样本的似然概率。
(4)参考贝叶斯公式计算出每个样本对于每种分布的后验概率。
(5)根据每个样本属于每种分布的后验概率
- 更新每种分布的参数(均值与方差),以提高似然概率值;
- 简单来说将样本的后验概率作为权重,使得更新后的分布更接近“属于”(higher posterior probability)它的样本特征。
- 更新先验概率
- 如果有很多的样本对于特征分布有较高的后验概率,将具有较高的先验概率。
(6)重复步骤(3),如果总体似然概率的增幅小于预设的阈值(收敛),则结束;否则继续执行步骤4、5、6,不断更新高斯分布,提高似然概率(最大化)。
参考下图,EM算法主要分为两步:Expectation Step(对应上述步骤3、4);Maximization Step(对应上述步骤5)
1.2 mclust包#
mclust包是基于EM算法实现混合分布聚类的常用R包,现在已经更新的5.4.10。
官方示例教程:https://cran.r-project.org/web/packages/mclust/vignettes/mclust.html
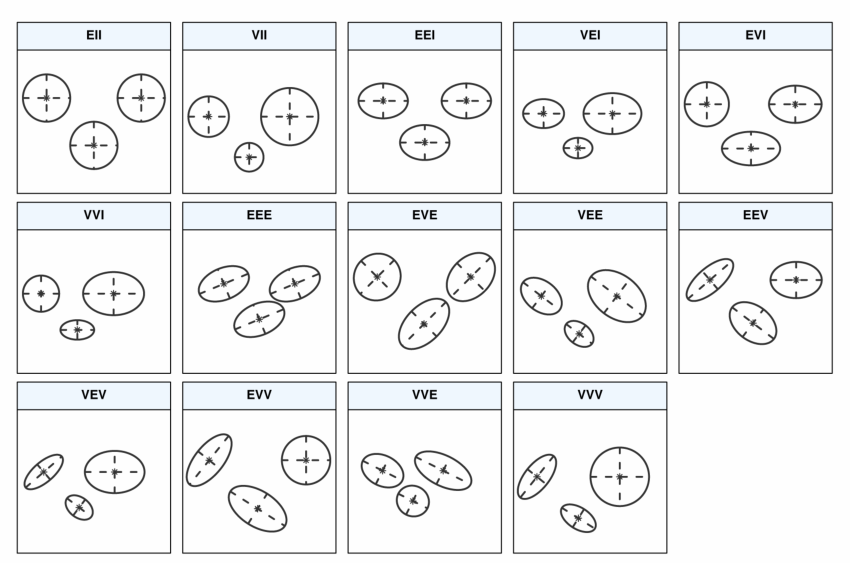
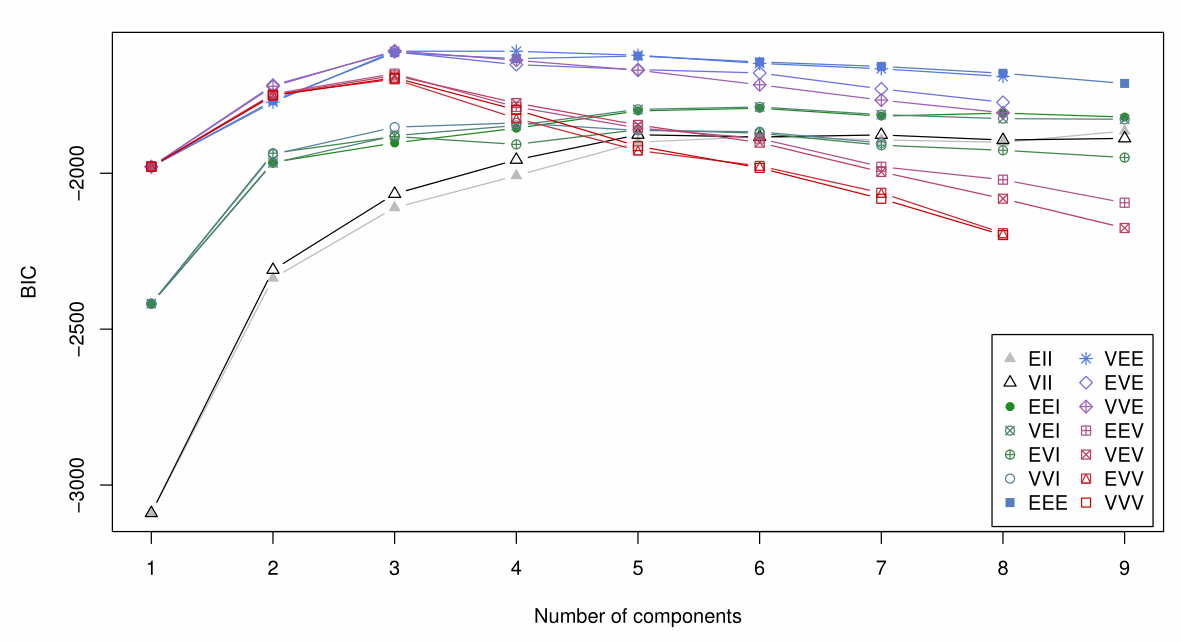
(1)在具体计算中,每一种Mclust模型结果由聚类数量与混合类型两个参数决定。其中混合类型表示:对于不同类型混合的高斯分布,使用3个字母组合表示14种特征的混合高斯分布。
- 第一个字母:(1)E表示等体积,V表示不同体积;
- 第二个字母:(1)E表示等长径比,V表示不同长径比,I表示球形;
- 第三个字母:(1)I表示与轴方向正交,E表示不正交,V表示每个分布方向不同。
(2)对于不同Mclust模型的结果,可通过BIC(贝叶斯信息准则)指标进行比较。在模型的似然概率结果的基础上,进一步考虑模型的参数。如果模型中包含太多的参数,BIC就会对模型进行惩罚。
- 简单来说在
Mclust()结果中,特定模型的BIC指标越小,表示该模型性能越好。
2、R实操#
2.1 多变量数据#
(1)基础操作#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
library(mclust)
data(banknote, package = "mclust")
table(banknote$Status)
# counterfeit genuine
# 100 100
swissTib <- select(banknote, -Status) #仅保留特征数据
dim(swissTib)
# [1] 200 6
head(swissTib)
# Length Left Right Bottom Top Diagonal
# 1 214.8 131.0 131.1 9.0 9.7 141.0
# 2 214.6 129.7 129.7 8.1 9.5 141.7
# 3 214.8 129.7 129.7 8.7 9.6 142.2
# 4 214.8 129.7 129.6 7.5 10.4 142.0
# 5 215.0 129.6 129.7 10.4 7.7 141.8
# 6 215.7 130.8 130.5 9.0 10.1 141.4
|
- 在不设置其它参数的情况下,
Mclust()默认计算1至9种聚类的14种混合类型的BIC指标结果;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
swissMclust <- Mclust(swissTib)
##(1) 结果概况
summary(swissMclust)
# ----------------------------------------------------
# Gaussian finite mixture model fitted by EM algorithm
# ----------------------------------------------------
#
# Mclust VVE (ellipsoidal, equal orientation) model with 3 components:
#
# log-likelihood n df BIC ICL
# -663.3814 200 53 -1607.574 -1607.71
#
# Clustering table:
# 1 2 3
# 18 98 84
#具体展示每种分布模型的分布特征
summary(swissMclust, parameters = TRUE)
##(2) 所有模型的BIC结果
dim(swissMclust$BIC)
# [1] 9 14
##(3) 最优模型的特征
swissMclust$G
# [1] 3
swissMclust$modelName
# [1] "VVE"
##(4) 模型计算结果可视化
#所有模型组合的BIC指标
plot(swissMclust, what = "BIC")
# plot(swissMclust, what = "classification")
# plot(swissMclust, what = "uncertainty")
# plot(swissMclust, what = "density")
|
(2)相关参数设置#
1
2
3
4
5
6
7
8
9
10
11
12
|
swissMclust2 <- Mclust(swissTib, G=1:3, modelNames = "VVE")
summary(swissMclust2)
swissMclust2$BIC
# Bayesian Information Criterion (BIC):
# VVE
# 1 -1978.941
# 2 -1721.311
# 3 -1607.574
#
# Top 3 models based on the BIC criterion:
# VVE,3 VVE,2 VVE,1
# -1607.574 -1721.311 -1978.941
|
1
2
3
4
5
6
|
hc1 <- hc(swissTib, modelName = "VVV", use = "SVD")
# hc2 <- hc(swissTib, modelName = "VVV", use = "VARS")
# hc3 <- hc(swissTib, modelName = "EEE", use = "SVD")
# swissMclust <- Mclust(swissTib, initialization = list(hcPairs = hc1)) #default
swissMclust <- Mclust(swissTib, initialization = list(hcPairs = hc2))
summary(swissMclust)
|
(3)Bootstrap法验证#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
bootClust <- MclustBootstrap(swissMclust)
summary(bootClust, what = "ci")
# summary(bootClust, what = "se")
# plot(bootClust, what = "mean")
# plot(bootClust, what = "pro")
# ----------------------------------------------------------
# Resampling confidence intervals
# ----------------------------------------------------------
# Model = VVE
# Num. of mixture components = 3
# Replications = 999
# Type = nonparametric bootstrap
# Confidence level = 0.95
#
# Mixing probabilities:
# 1 2 3
# 2.5% 0.05396204 0.4200456 0.3549896
# 97.5% 0.13491555 0.5550405 0.4852951
# ....
|
2.2 单变量#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
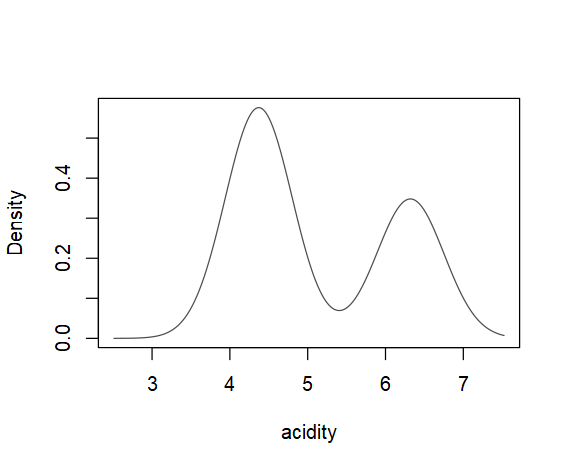
data(acidity)
str(acidity)
# num [1:155] 2.93 3.91 3.73 3.69 3.82 ...
acidityMclust <- Mclust(acidity)
summary(acidityMclust, parameters = TRUE)
# ----------------------------------------------------
# Gaussian finite mixture model fitted by EM algorithm
# ----------------------------------------------------
#
# Mclust E (univariate, equal variance) model with 2 components:
#
# log-likelihood n df BIC ICL
# -185.9493 155 4 -392.0723 -398.5554
#
# Clustering table:
# 1 2
# 98 57
#
# Mixing probabilities:
# 1 2
# 0.6233595 0.3766405
#
# Means:
# 1 2
# 4.370946 6.320153
#
# Variances:
# 1 2
# 0.1863702 0.1863702
table(acidityMclust$classification)
# 1 2
# 98 57
plot(acidityMclust, what = "density")
|