1、层次聚类简介

1.1 计算步骤

层次聚类hierarchical clustering常用的是自下而上的聚合法(Agglomerative)。与之相对的是自顶而下的分裂法(Division)。

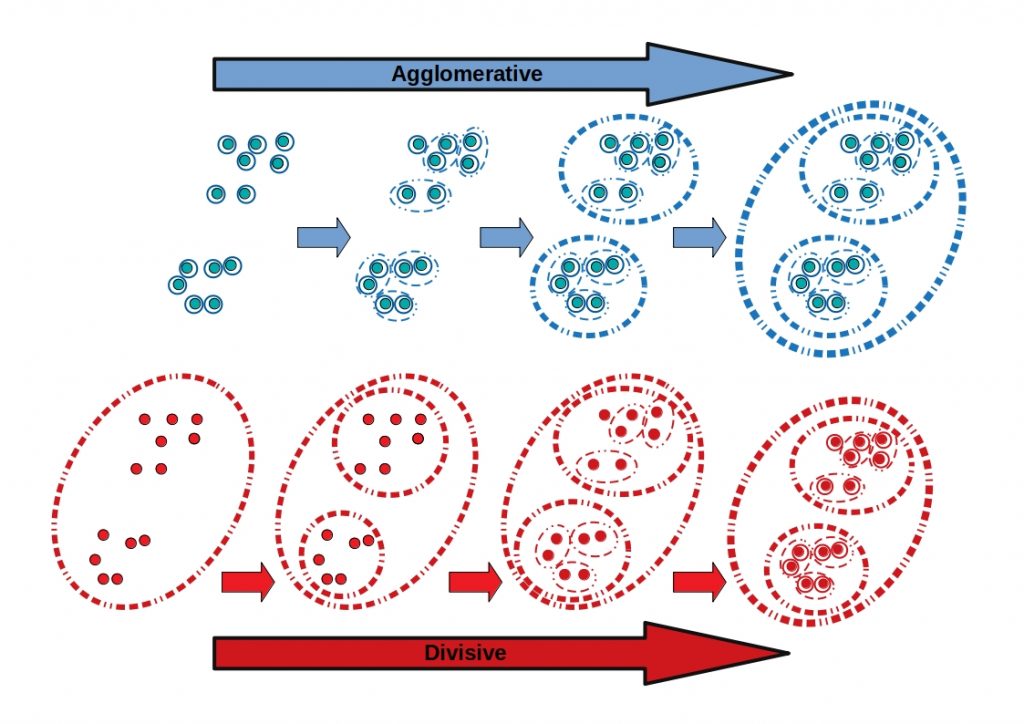
What does HCA stand for? The figure compares the agglomerative and divisive calculation.

以聚合法为例：最初将数据集中每个单独样本视为一个聚类

（1）计算所有聚类两两之间的距离，通常为欧几里得距离。

（2）将最相似(距离最近)的两个聚类合并成一个聚类。

（3）重复上述步骤1、2，直至所有的所有样本都位于单个聚类中。

1.2 聚类距离

计算聚类之间的距离，有如下方式可供选择

  • 质心链接：两聚类质心之间的距离；
  • 单链接：两聚类最近样本之间的距离；
  • 全链接：两聚类最远样本之间的距离；
  • 均链接：两聚类所有样本之间距离的平均值；
  • Ward方法：
    • 首先计算每个聚类的类内距离平方和（类内方差）
    • 然后对于所有聚类两两组合中，类内方差增加最少的组合方式。
Chapter 17. Hierarchical clustering - Machine Learning with R, the tidyverse, and mlr

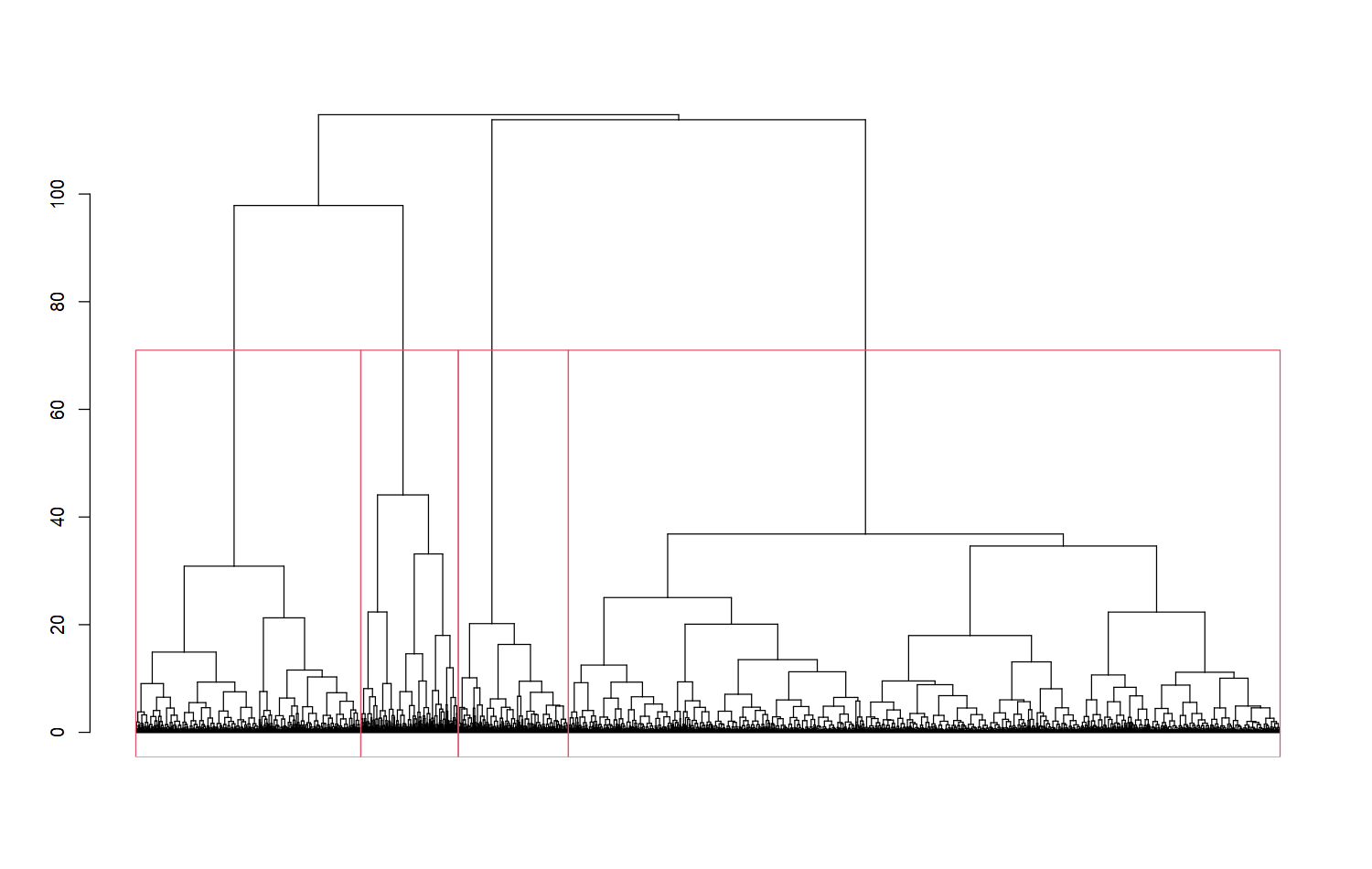
1.3 树状图切割聚类

对于层次聚类的结果通常以树状图(dendrogram)的方式展示。如下左图表示原始样本的分布情况；右图表示层次聚类的结果

  • 水平线表示相应的两个聚类被合并在一起，而这两个聚类之间的距离对应水平线的高度。

层次聚类的优势在于保留了样本之间的层次结构，即样本与哪些样本更相似性，而又与哪些样本的关系比较远。

  • 如下示例，从层次聚类结果来看，样本C更接近DEF，与AB较远

基于层次聚类结果，确定样本聚类的划定方式就是在树状图使用水平线切割，有如下两种思路

  • 给定指定的距离进行切割；
  • 给定指定的聚类数进行切割。
What is Hierarchical Clustering? | Displayr.com

如上的聚类确定方式需要对数据集有预期的把握。如不确定，可比较不同的聚类结果的性能(上一节K均值算法中提到的聚类性能评价指标)，选择最优的聚类结果。

2、代码实操

  • (1) 原始数据归一化
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

data(GvHD, package = "mclust")
gvhdTib <- GvHD.control
#   CD4 CD8b CD3 CD8
# 1 199  420 132 226
# 2 294  311 241 164
# 3  85   79  14 218
gvhdScaled <- gvhdTib %>% scale()
#          CD4       CD8b        CD3        CD8
# 1 -0.4373389  0.8752503 -0.2166459  0.1832758
# 2  0.2595066  0.1289858  0.5752226 -0.3543201
# 3 -1.2735535 -1.4593936 -1.0738981  0.1139086
  • (2) 计算样本两两间距离
1
2
3
4
5

gvhdDist <- dist(gvhdScaled, method = "euclidean")
dim(gvhdDist)
# [1] 6809 6809
# dist_mt = as.matrix(gvhdDist)
# dist_mt[1:4,1:4]
  • (3) 层次聚类
1
2
3
4

gvhdHclust <- hclust(gvhdDist, method = "ward.D2")

#可视化
plot(as.dendrogram(gvhdHclust), leaflab = "none")
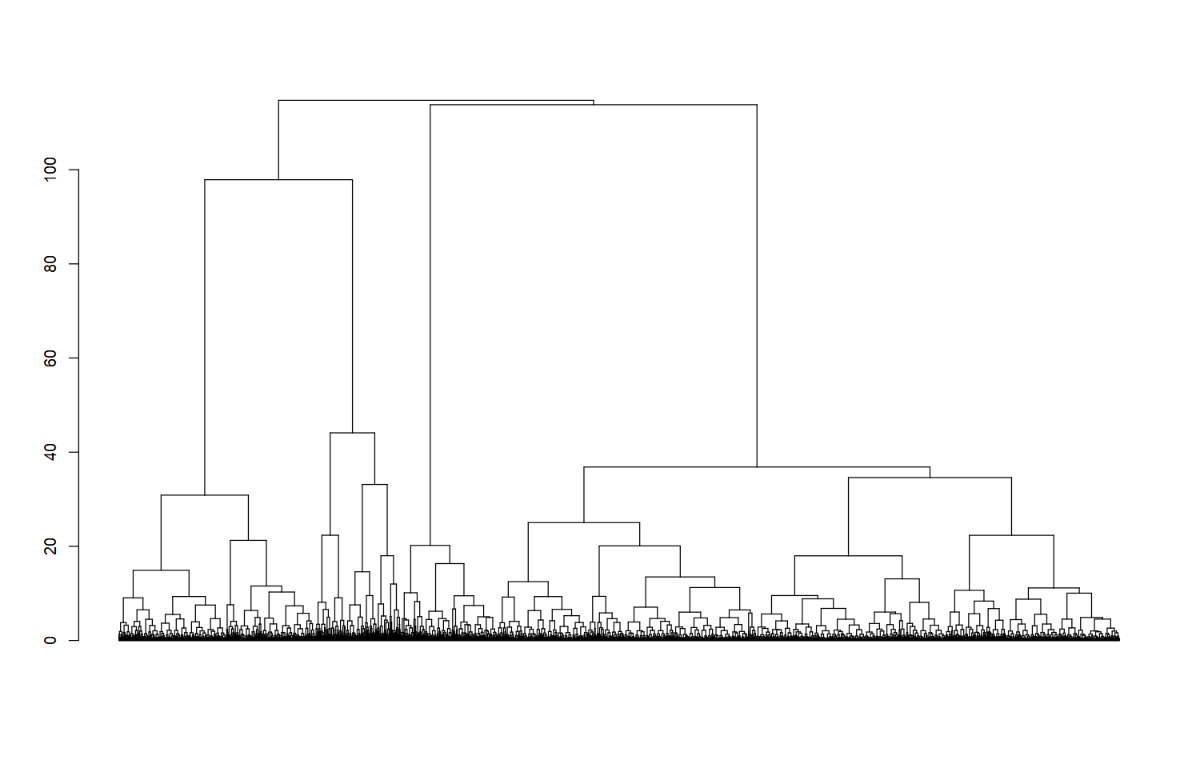
image-20220608223153314
  • (4) 确定聚类
1
2
3
4
5
6
7
8

gvhdCut <- cutree(gvhdHclust, k = 4)   #也可使用 h= 参数指定切割的高度
gvhdTib <- mutate(gvhdTib, gvhdCut = as.factor(gvhdCut))
head(gvhdTib)
table(gvhdTib$gvhdCut)
#    1    2    3    4 
# 4235 1339  580  655

rect.hclust(gvhdHclust, k = 4)

image-20220608223758441