1、算法简介

1.1 不同种K均值算法

k均值是常用的聚类算法之一。

（1）首先需要预先定义样本集中存在多少种聚类（假设为k），即数据集中处在K个真正意义上的质心。

（2）然后随机初始化k个质心，每个质心具有与样本数据相同维度的变量值。

（3）最后通过不断迭代，使这些初始质心点向数据集中真正意义上的质心点处移动，直到得到预期的聚类结果，

k-均值算法有多种实现形式，即不同的迭代方式。常见有如下几种

Lloyd方法

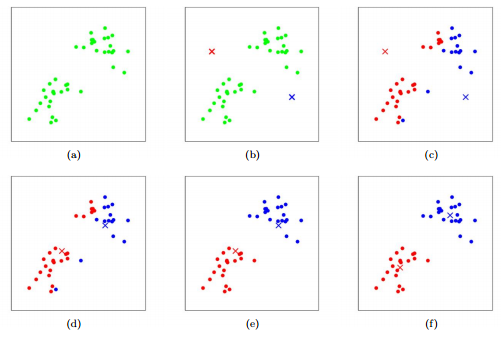
如下图所示

（1）预设设定数据集样本可以聚为2类，随机初始化两个质心点。[如下图b]

（2）计算所有样本与当前2个质心的距离，通常为欧几里得距离。

（3）将样本分配给相距最近的质心所表示的聚类。[如下图c]

（4）将每个质心放在聚类内样本的均值位置。[如下图d]

（5）重复上述步骤（3）~（4），直到没有样本改变聚类或者达到最大迭代次数位置。[如下图e、f]

CS221

由于涉及两点之间欧几里得距离的计算，需要先对数据进行归一化处理。下同

MacQueen方法

（1）预设设定数据集样本可以聚为3类，随机初始化3个质心点。

（2）计算所有样本与当前3个质心的距离，通常为欧几里得距离。

（3）将样本分配给相距最近的质心所表示的聚类，然后将质心放到对应聚类的中心位置。

（4）对于所有样本逐一完成下述操作

  • A：计算样本与当前3个质心的距离；
  • B：将样本分配给相距最近的质心所表示的聚类；
  • C：如果样本改变聚类，更新有变动的聚类内的质心位置。
    • 对于改变类别的样本，该样本的原聚类就缺失一个样本；而新聚类就增多一个样本。

（5）重复上述步骤（3）~（4），直到没有样本改变聚类或者达到最大迭代次数位置。

如上Lloyd算法与Macqueen算法主要的区别在于更新、移动质心位置。

  • 前者是一次性给所有样本分配新聚类标签，然后更新所有质心位置；
  • 后者是逐一给样本分配新聚类标签，然后逐一更新质心位置。

此外还有一种Hartigan-Wong算法基于最小化聚类误差平方和，更新、迭代质心的位置；相对来说，计算成本最高。

1.2 聚类评价指标

聚类clusteing通常属于无监督学习。在优化超参数时，需要寻找一个能够度量聚类性能的指标。下面介绍其中两种常用的指标。

Davies-Bouldin指标

核心是评价每个聚类与其它聚类的可区分性。

（1）对于得到的K个聚类，计算每个聚类自身的散度，即聚类内样本到质心距离的均方差。用以评价聚类的分散程度S。

i：k个聚类中的第i个聚类；Ti表示该聚类的样本点数；Ai表示该聚类的质心；Xj表示该聚类的第j个样本点坐标（多维）。

$$ S_i = ( \frac{1}{T_i} \sum_{j=1}^{T_i}||X_j-A_i|| ) $$ （2）对于每个聚类，逐一进行如下计算

  • ① 计算特定聚类的质心与其余聚类质心的距离；

    Ai与Aj聚类i与聚类j的质心，n表示每个数据点的维度（或者变量数）

$$ M_{i,j} = ||A_i-A_j|| = (\sum_{k=1}^{n}|a_{k,i}-a_{k,j}|^2)^{\frac{1}{2}} $$

数学符号 ：一对竖线|x|，内为实数，表示绝对值；一对双竖线||Ai - Aj||默认求L2范数，即两个向量对应每个元素平方和的平方根

  • ② 计算特定聚类与其余聚类的可分性R：分子–两个聚类的散度和；分母–两个聚类的质心距离。
    • 该值越小，表示两个聚类的可分性越好。

$$ R_{i,j} = \frac{S_i+S_j}{M_{i,j}} $$

  • ③ 取特定聚类与其余聚类可分性最差的结果，即为该聚类的间隔比率D。 $$ D_i=\max_{j\neq i}R_{i,j} $$

（3）计算所有聚类的间隔比率的平均值作为Davies-Bouldin index，用以评估聚类性能。、

  • DB指标越小，聚类性能越好。

$$ DB=\frac{1}{N}\sum_{i=1}^{N}D_i $$

img

silhouette指标

又称轮廓系数，核心是评价每个样本的当前分类的性能。

（1）计算特定样本i到所在聚类CI内其它样本的平均距离a。值越小，表明该样本越接近所在聚类。

$$ a(i) = \frac{1}{|C_I|-1}\sum_{j\in C_I,i\neq j}d(i,j) $$

（2）计算特点样本i到其它各个聚类内样本的平均距离b，取最小值。值越小，表明该样本越接近该聚类。 $$ b(i) = \min_{J\neq I} \frac{1}{|C_J|}\sum_{j\in C_j}d(i,j) $$

（3）据此计算样本i的轮廓系数s。

  • 越接近1（b大，a小），表明该样本当前所在的聚类越合适；
  • 越接近-1（b小，a大），表明越不符合当前聚类。

$$ s(i) = \frac{b(i)-a(i)}{max{a(i),b(i) }} $$ The Silhouette Loss Function: Metric Learning with a Cluster Validity Index

（4）最后取所有样本的轮廓系数的均值，作为该聚类性能的度量。

  • silhouette平均指标越大，表示聚类性能越好

此外还有pseudo-F指标类似于方差分析。计算两两聚类之间的F统计量：聚类之间的距离平方和(组间方差)与聚类内的距离平方和(组内方差)。pseudo-F值越大，表明两聚类间的可分性越好。

1.3 超参数

关于K均值算法的超参数主要是聚类的K值。即对数据潜在的聚类数也不太确定时，可以遍历一定范围的K值，选择使得聚类性能指标最好的聚类。

其次可选的超参数包括不同的K均值算法、最大迭代次数、随机初始质心组数

  • （1）不同的K均值算法：包括如上所述的3种
  • （2）最大迭代次数。K均值迭代停止的条件有2个：要么没有样本改变聚类；要么已达到最大迭代次数。
  • （3）随机初始质心组数：在开始迭代前，通过初始化多组质心，选择初始聚类中平方误差和最小的质心组可有效降低需要迭代的次数。

2、mlr建模

1
2

library(mlr3verse)
library(tidyverse)

2.1 细胞的4种基因表达量数据

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

data(GvHD, package = "mclust")
head(GvHD.control)
#   CD4 CD8b CD3 CD8
# 1 199  420 132 226
# 2 294  311 241 164
# 3  85   79  14 218
# 4  19    1 141 130
# 5  35   29   6 135
# 6 376  346 138 176
#由于涉及距离的计算，需要将数据归一化
gvhdScaled <- GvHD.control %>% scale()

2.2 确定聚类任务与训练方法

  • 根据5种基因表达特征，使用k均值方法将细胞分为若干类
1

task_clust = as_task_clust(gvhdScaled)
  • 确定需要遍历的超参数组合
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

learner = lrn("clust.kmeans")
learner$param_set
# <ParamSet>
#           id    class lower upper nlevels       default value
# 1:   centers ParamUty    NA    NA     Inf             2     2
# 2:  iter.max ParamInt     1   Inf     Inf            10      
# 3: algorithm ParamFct    NA    NA       4 Hartigan-Wong      
# 4:    nstart ParamInt     1   Inf     Inf             1      
# 5:     trace ParamInt     0   Inf     Inf             0   

# centers : 聚类数
# iter.max: 迭代次数
# nstart : 随机初始多少组质心 
# algorithm : k均值算法

##(1) 对于nstart、iter.max 建议先确定固定值
##(2) 对于algorithm、centers可设置多个候选值组合。
search_space = ps(
  algorithm = p_fct(c("Hartigan-Wong", "Lloyd", "MacQueen")),
  centers = p_int(lower=3,upper=8),
  iter.max = p_int(lower=100,upper=100),
  nstart = p_int(lower=5,upper=5)
)
design = expand.grid(algorithm = c("Hartigan-Wong", "Lloyd", "MacQueen"),
                     centers = 3:8,
                     iter.max = 100,
                     nstart = 5,
                     stringsAsFactors = FALSE) %>% as.data.table()

## 交叉验证与评价指标
resampling = rsmp("cv")
grep("clust",mlr_measures$keys(), value = T)
# [1] "clust.ch"         "clust.db"         "clust.dunn"       "clust.silhouette" "clust.wss"
measure = msr("clust.silhouette")

2.3 优化超参数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

##创建实例
instance = TuningInstanceSingleCrit$new(
  task = task_clust,
  learner = learner,
  resampling = resampling,
  measure = measure,
  terminator = trm("none"),
  search_space = search_space
)
tuner = tnr("design_points", design = design)  
tuner$optimize(instance)

as.data.table(instance$archive)[,1:5] %>% head()
#        algorithm centers iter.max nstart clust.silhouette
# 1: Hartigan-Wong       3      100      5        0.4529947
# 2:         Lloyd       3      100      5        0.4678896
# 3:      MacQueen       3      100      5        0.4680556
# 4: Hartigan-Wong       4      100      5        0.4944346
# 5:         Lloyd       4      100      5        0.4943383
# 6:      MacQueen       4      100      5        0.4944346

instance$result_learner_param_vals      #最佳超参数
# $centers
# [1] 4

# $algorithm
# [1] "Hartigan-Wong"

# $iter.max
# [1] 100

# $nstart
# [1] 5

instance$result_y                       #最佳超参数的CV结果
# clust.silhouette 
# 0.4944346

2.4 确定模型

1
2
3

learner$param_set$values = instance$result_learner_param_vals
learner$train(task_clust)
learner$model