算法简介

t-SNE

正态分布密度函数，其中σ表示标准差，μ表示均值

第一步：计算高维空间中任意两样本点的欧几里得距离。

第二步：对于任一特定节点，将其余节点与之的距离转换为以该节点为中心的正态分布的概率值。

正态分布的标准差与该样本点周围数据的密度成反比，但是具体关系依赖perplex超参数。该值越大表明越关注数据的全局特征，反之越关注数据的局部结构。

第三步：将对任一特点节点的其余节点概率处于它们的和，从而使得数据集中每个样本的概率总和为1。

$$ 正态分布密度函数 \quad f(x) = \frac{1}{\sigma \sqrt{2\pi}}exp(\frac{-(x-\mu)^2}{2\sigma^2}) $$

$$ 样本点j到点i的概率 \quad P_{j|i} = \frac{exp(-(||x_i-x_j||)^2 /2\sigma_i^2)}{\sum_{k\neq i}exp(-(||x_i-x_j||)^2 /2\sigma_i^2)} $$

其中||Xi-Xj||表示高维空间中数据点i与数据点j的欧几里得距离

如上以所以样本点均为中心样本进行正态分布密度转换之后，可以得到一个概率矩阵p，用以描述每个样本与其它样本的相似程度。

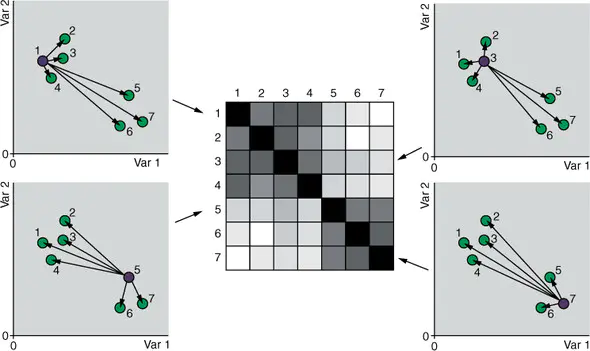
在二维的空间中，对所有数据点重新排布。使用上述方法再次计算新的概率矩阵与q。使用损失函数KL散度评价两个概率矩阵的相似性。采用梯度下降的方法，不断迭代的、”移动“二维空间中数据点的位置，使得KL散度指标逐渐降低，直至达到预期水平。

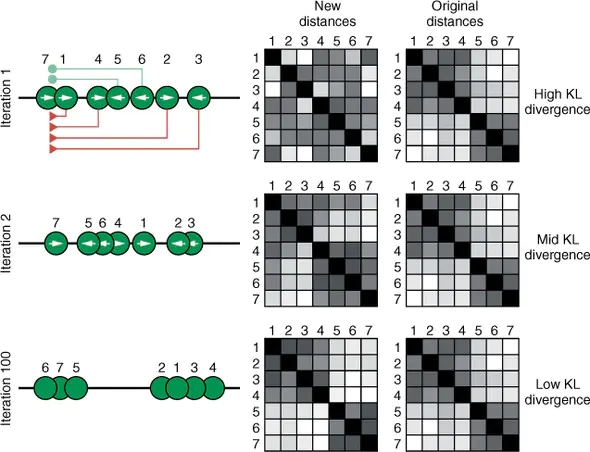
t-SNE中的t的含义是指在计算新的、二维空间中样本间的概率矩阵时，使用T分布将样本距离转换为概率值可以更好的兼容离群点的影响，识别出真正距离相近的样本。

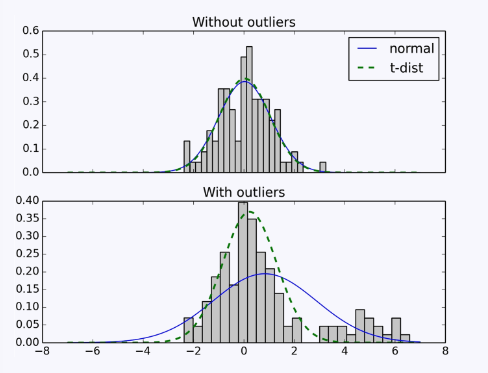
UMAP

UMAP的思路与tSNE类似，将样本在高维空间中的距离转换到二维平面中。与tSNE不同的是UMAP采用了所谓流形的概念，测量流形中样本之间的距离。

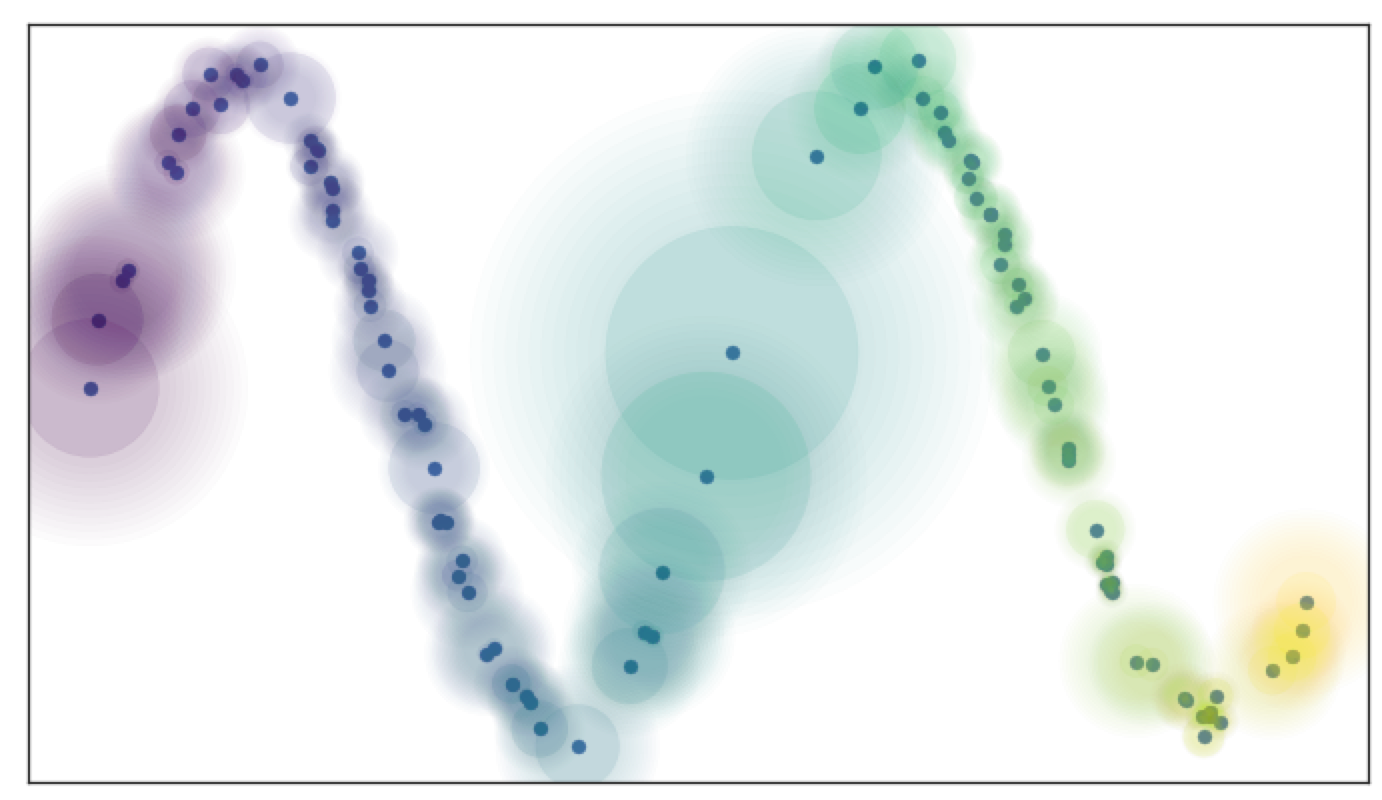
在学习流形时，有两个关键步骤

（1）对于既定的样本点进行局部连接，扩展最近的样本（local_connectivity=1），这样可以确保不存在孤立的样本。

（2）然后以局部连接样本为边界进行模糊扩展，确定近邻样本。可通过超参数设置，较大的值表示包含更多的近邻样本，更关注全局结构；反之更关注局部结构。

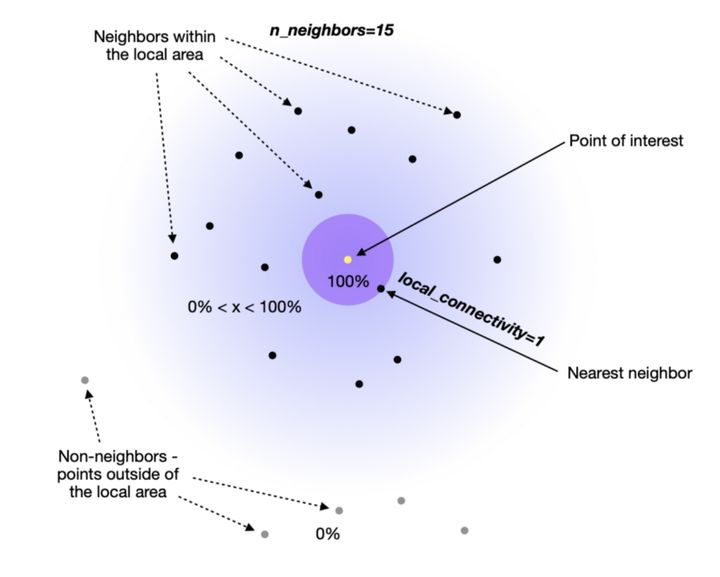
计算如此得到的流形中，得到所有样本与近邻样本之间的距离。下一步将数据放在两个维度的流形中，并迭代地移动数据点，直至新流形中样本间的距离等于沿着原始高维流形中样本间的距离。损失函数为交叉熵。

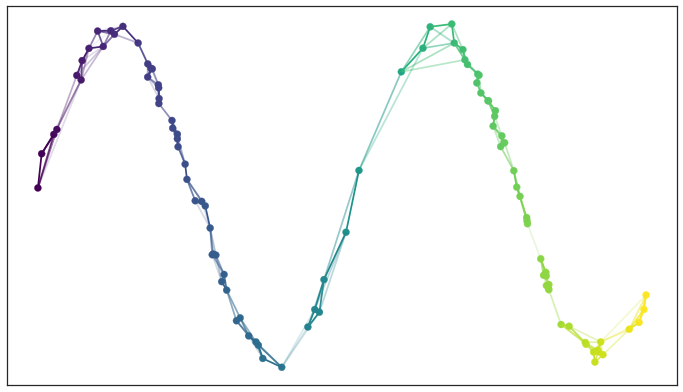
二者比较

（1）tSNE与UMAP相对于PCA均属于非线性降维方式，获得的二维平面新轴不能用原始变量直接解释

（2）相比于tSNE，UMAP的具有更多的优势：计算开销小、同时保留了局部与全局结构；而且作为一种确定性算法，给定相同的输入可以给出相同的输出。

（3）对于tSNE，关注的更多是局部结构，即聚为一类的数据点具有很好的相似性；但是不同聚类之间的距离并没有任何含义。

（4）在实际分析时，往往先对高维数据进行PCA分析，然后对于保留的若干主成分再进行tSNE/UMAP降维

代码实操

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


library(tidyverse)
data(banknote, package = "mclust")
swissTib = as_tibble(banknote)
# # A tibble: 6 x 7
# Status  Length  Left Right Bottom   Top Diagonal
# <fct>    <dbl> <dbl> <dbl>  <dbl> <dbl>    <dbl>
# 1 genuine   215.  131   131.    9     9.7     141 
# 2 genuine   215.  130.  130.    8.1   9.5     142.
# 3 genuine   215.  130.  130.    8.7   9.6     142.
# 4 genuine   215.  130.  130.    7.5  10.4     142 
# 5 genuine   215   130.  130.   10.4   7.7     142.
# 6 genuine   216.  131.  130.    9    10.1     141.
dat = swissTib[,-1]

1、t-SNE

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


library(Rtsne)
?Rtsne
##(1) 相关参数[一般使用默认参数即可，这里主要了解一下]
# perplexity = 30   # 5~50 值越大表示越保留全局特征（相对而言）
# theta = 0.        # 0~1 速度与精确度的平衡，越大越关注速度
# max_iter = 1000   # 迭代次数
# eta = 200         # 每次迭代，点移动的距离
# num_threads = 1   # 使用线程数
# pca = TRUE        # 进行tSNE分析前，是否进行PCA分析
# initial_dims = 50 # 若进行PCA分析，保留的主成分数
# dims = 2          # 输出的tSNE维度数

##(2) 示例分析
set.seed(123) #设置随机种子，确保分析结果的一致性
tsne.list = Rtsne(dat)
tsne = tsne.list$Y %>% as.data.frame()
colnames(tsne) = c("tSNE_1","tSNE_2")
head(tsne)
#       tSNE_1     tSNE_2
# 1  -8.127869  5.0456539
# 2 -14.330835  4.5799939
# 3 -13.687125  5.9405066
# 4 -13.203127 -0.3737462
# 5 -12.773563  8.5912141
# 6  -8.431319  4.1007125
tsne$label = swissTib$Status
ggplot(tsne, aes(x=tSNE_1,y=tSNE_2,color=label)) + 
  geom_point()

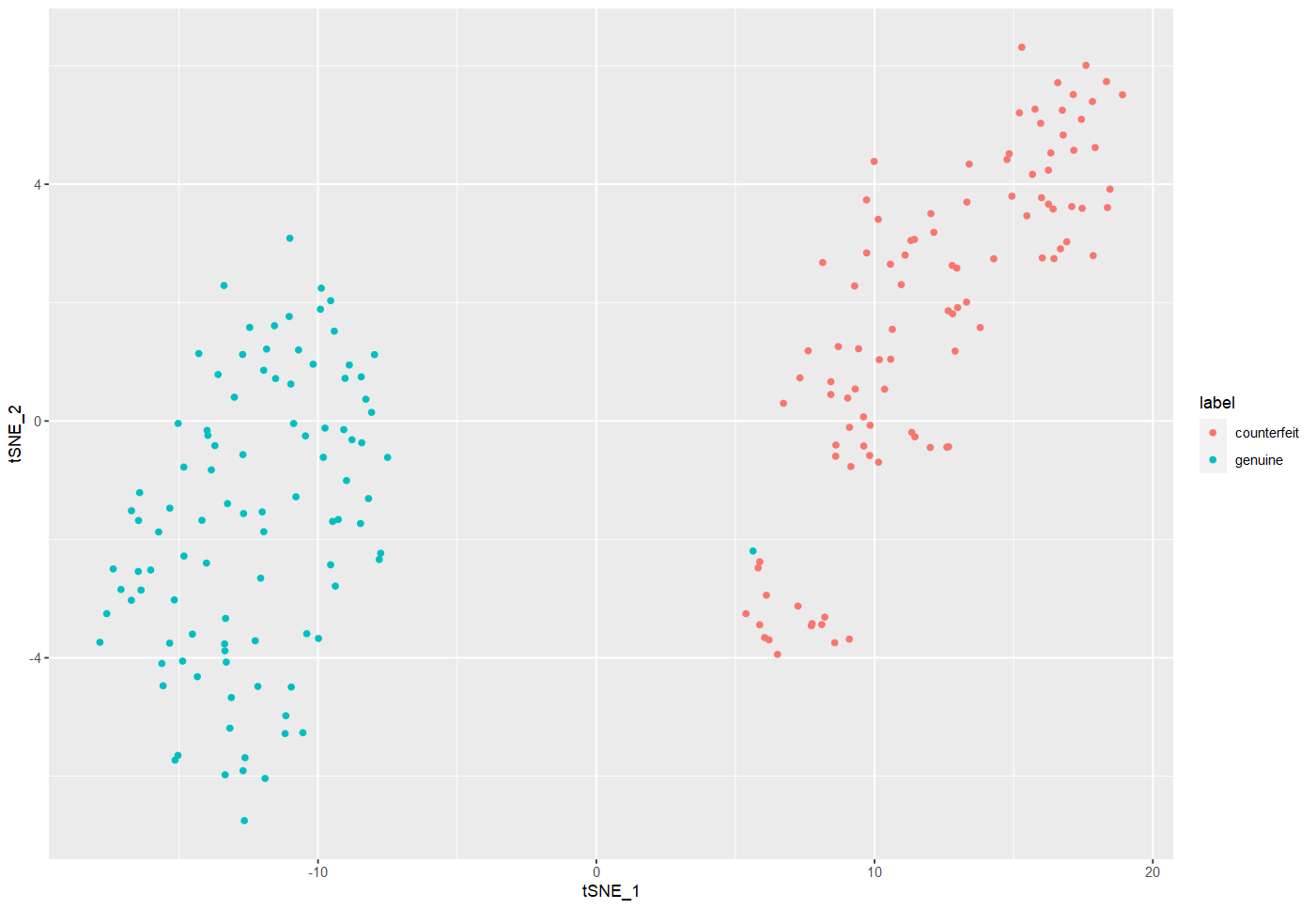
2、UMAP

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43


library(umap)
##(1) 查看默认参数
umap::umap.defaults
# umap configuration parameters
# n_neighbors: 15      #控制模糊搜索区域的半径，较大值的将包含更多的近邻样本，即更考虑全局结构
# n_components: 2      #输出维度数
# metric: euclidean    #测量流形上样本的距离
# n_epochs: 200        #迭代次数
# input: data
# init: spectral
# min_dist: 0.1
# set_op_mix_ratio: 1
# local_connectivity: 1
# bandwidth: 1
# alpha: 1
# gamma: 1
# negative_sample_rate: 5
# a: NA
# b: NA
# spread: 1
# random_state: NA
# transform_state: NA
# knn: NA
# knn_repeats: 1
# verbose: FALSE
# umap_learn_args: NA

##(2) 示例分析
#不需要设定随机种子也能保证结果的一致性
umaps.list = umap(dat)
umaps = umaps.list$layout %>% as.data.frame()
colnames(umaps)=c("UMAP_1","UMAP_2")
head(umaps)
#      UMAP_1    UMAP_2
# 1  1.407095 -4.126555
# 2  1.213177 -6.306884
# 3  1.980743 -6.008990
# 4 -1.303874 -6.129523
# 5  2.664741 -5.839394
# 6  1.355476 -4.351818
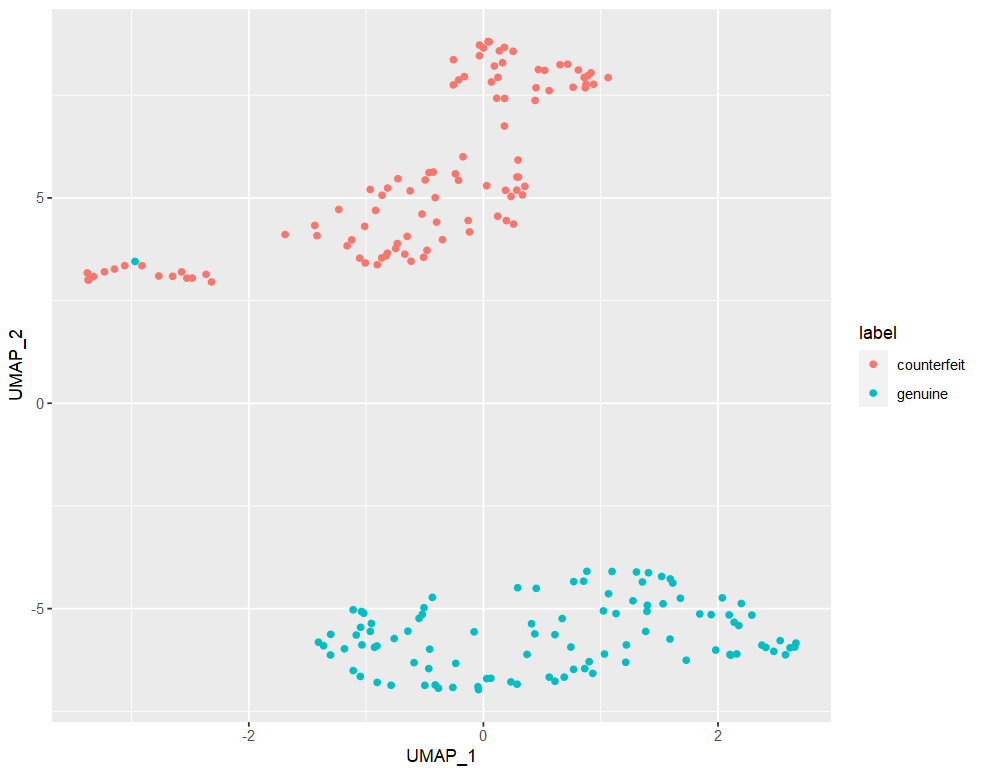
umaps$label = swissTib$Status
ggplot(umaps, aes(x=UMAP_1, y=UMAP_2, color=label)) + 
  geom_point()

算法简介#

t-SNE#

UMAP#

二者比较#

代码实操#

1、t-SNE#

2、UMAP#