降维是指在保留尽可能多原始数据条件下,将许多变量(成百上千)转换为少数的、不相关的变量,从而有利于后序的数据分析与可视化。而主成分分析(PCA, Principal Component Analysis)是最常用的无监督降维算法。
1、关于降维#
1.1 高维数据的不利影响#
(1)稀疏性#
又称维数灾难, curse of dimensionality
当同样样本量的数据在从一维变成二维,再到三维的过程中,样本逐渐变得稀疏。机器学习模型难以从中学习模式,相反较容易收到噪声影响(离群点)。
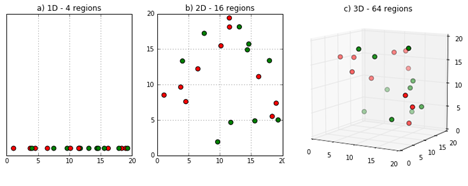
(2)共线性#
当变量越来越多时,更容易出现具有不同程度相关性的样本。
当两个变量高相关时,则称这两个变量具有共线性;当存在两个以上变量相关时,称具有多重共线性。
共线性的出现会对某些机器学习算法产生负面影响,主要是对线性回归的参数估计有不利影响。但如果主要关注预测精度,共线性则不是大问题。
1.2 最大化方差的PCA#
基于方差最大化的PCA降维聚类方法可有效解决高维度数据所带来的的不利影响
1.2.1 步骤#
(1)中心化/标准化#
(1)中心化,又称Zero-centered,是指每个变量减去的所有样本均值。中心化处理后的变量均值等于0。
$$
x - \overline{x}
$$
(2)标准化,又称归一化Standardization/Normalization,是指在中心化的基础上进一步除以标准差。标准化后的变量均符合均值为0,方差为1的标准正态分布。即拥有相同的尺度。
$$
\frac{x - \overline{x}}{\sigma}
$$
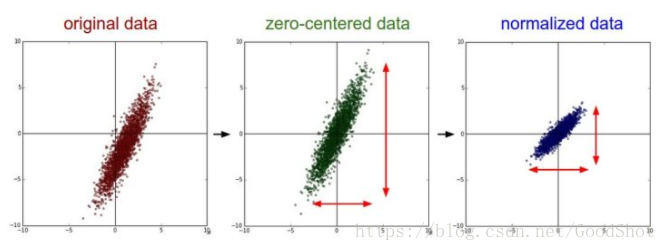
在PCA分析时,中心化是必要的。但是如果预测变量本身的尺度就相似,那么可以不进行标准化
(2)寻找主成分#
首先先寻找第一主成分,需要满足两个条件:①穿过原点;②样本点投影到轴上的方差最大。
第二个条件很重要,含方差分解的思想,找出能够尽可能多解释数据总方差的潜在变量。这些潜在变量(主成分)实际上是预测变量的线性组合。
$$
C_i = w_{i1}x_{1} + w_{i2}x_{2} + … + w_{ip}x_{p}
$$
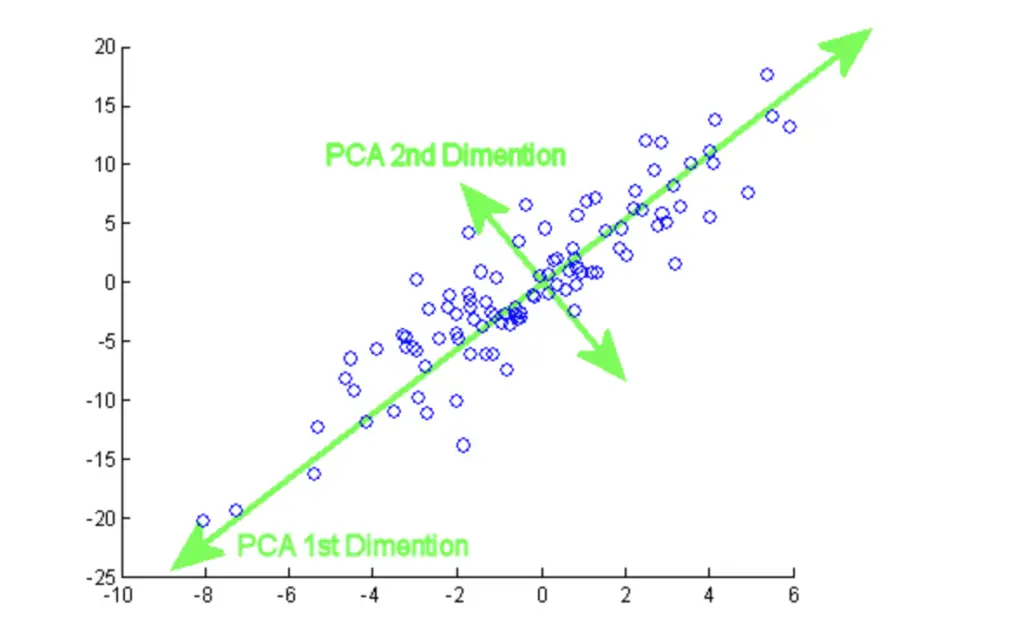
然后继续寻找第二主成分,除了上述两个条件外,还需要满足第三条件③与上一个主成分轴相互垂直,从而得到一组彼此间不相关的主成分。
一般来说,第一主成分能够解释最多的方差,其余主成分依次减小。
(3)保留TopN主成分–降维#
基于上述找到的主成分轴,可以保留Top N个主成分,从而实现能够保留大部分数据信息的同时,达到降维的目的。而且这些主成分互不相关。
关于N值的选择,有一些经验方法。
①保留累计解释至少80%方差的主成分;
②保留所有特征值大于等于1的主成分;
③寻找elbow图中的拐点…
1.2.2 相关术语#
原始样本点投影到该主成分的方差
主成分的特征变量组合的权重值
每个原始变量与每个主成分之间的关联程度
2、PCA实操#
2.1 示例数据–真伪钞票#
- 如下包含100张真钞与100张假钞的特征数据
- 下面对这6个特征变量进行PCA降维
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
library(tidyverse)
library(tidyverse)
data(banknote, package = "mclust")
swissTib <- banknote
head(swissTib)
# Status Length Left Right Bottom Top Diagonal
# 1 genuine 214.8 131.0 131.1 9.0 9.7 141.0
# 2 genuine 214.6 129.7 129.7 8.1 9.5 141.7
# 3 genuine 214.8 129.7 129.7 8.7 9.6 142.2
# 4 genuine 214.8 129.7 129.6 7.5 10.4 142.0
# 5 genuine 215.0 129.6 129.7 10.4 7.7 141.8
# 6 genuine 215.7 130.8 130.5 9.0 10.1 141.4
table(swissTib$Status)
# counterfeit genuine
# 100 100
|
2.2 PCA降维#
- 使用stats包的
prcomp()函数
- 根据数据特点,进行中心化或者标准化。如果原始变量具有相同的尺度可不必标准化。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
#默认为center = TRUE, scale = FALSE
pca <- dplyr::select(swissTib, -Status) %>%
prcomp(center = TRUE, scale = TRUE)
##(1) 样本的主成分值
head(pca$x)
# PC1 PC2 PC3 PC4 PC5 PC6
# [1,] -1.7430272 -1.64669605 -1.4201973 -2.7479691 0.003293759 0.60202200
# [2,] 2.2686248 0.53744461 -0.5313151 -0.6573558 -0.158171742 0.45654268
# [3,] 2.2717009 0.10740754 -0.7156191 -0.3408384 -0.453880889 -0.04532905
# [4,] 2.2778385 0.08743490 0.6041176 -0.3918255 -0.282913485 -0.05543875
# [5,] 2.6255397 -0.03909779 -3.1883837 0.4240168 -0.277502895 0.72026433
# [6,] -0.7565089 -3.08101359 -0.7845117 -0.5980322 0.192757017 -0.10529393
##(2) 主成分的特征向量
pca$rotation
# PC1 PC2 PC3 PC4 PC5 PC6
# Length 0.006987029 -0.81549497 0.01768066 0.5746173 -0.0587961 0.03105698
# Left -0.467758161 -0.34196711 -0.10338286 -0.3949225 0.6394961 -0.29774768
# Right -0.486678705 -0.25245860 -0.12347472 -0.4302783 -0.6140972 0.34915294
# Bottom -0.406758327 0.26622878 -0.58353831 0.4036735 -0.2154756 -0.46235361
# Top -0.367891118 0.09148667 0.78757147 0.1102267 -0.2198494 -0.41896754
# Diagonal 0.493458317 -0.27394074 -0.11387536 -0.3919305 -0.3401601 -0.63179849
##(3) 主成分的特征值
summary(pca)
# Importance of components:
# PC1 PC2 PC3 PC4 PC5 PC6
# Standard deviation 1.7163 1.1305 0.9322 0.67065 0.51834 0.43460
# Proportion of Variance 0.4909 0.2130 0.1448 0.07496 0.04478 0.03148
# Cumulative Proportion 0.4909 0.7039 0.8488 0.92374 0.96852 1.00000
##Standard deviation表示特征值的平方根
##Proportion of Variance表示该主成分的方差解释占比
##Cumulative Proportion表示累计方差解释占比
##(4) 主成分的变量负载(与变量的相关性) = 特征向量 * 特征值的平方根
loadings = lapply(1:6, function(i){
pca$rotation[,i] * pca$sdev[i]
}) %>% do.call(cbind, .)
colnames(loadings) = colnames(pca$rotation)
loadings
# PC1 PC2 PC3 PC4 PC5 PC6
# Length 0.01199158 -0.9219364 0.01648225 0.38536590 -0.0304764 0.01349746
# Left -0.80279596 -0.3866019 -0.09637548 -0.26485400 0.3314768 -0.12940207
# Right -0.83526859 -0.2854104 -0.11510550 -0.28856524 -0.3183114 0.15174296
# Bottom -0.69810421 0.3009779 -0.54398559 0.27072283 -0.1116898 -0.20094033
# Top -0.63139786 0.1034278 0.73418921 0.07392333 -0.1139569 -0.18208461
# Diagonal 0.84690418 -0.3096965 -0.10615680 -0.26284740 -0.1763188 -0.27458160
|
2.3 可视化#
1
2
|
library(patchwork)
library(factoextra)
|
(1) 主成分与原始变量#
1
2
3
|
p1 = fviz_pca_biplot(pca, label = "var")
p2 = fviz_pca_var(pca)
p1 + p2
|
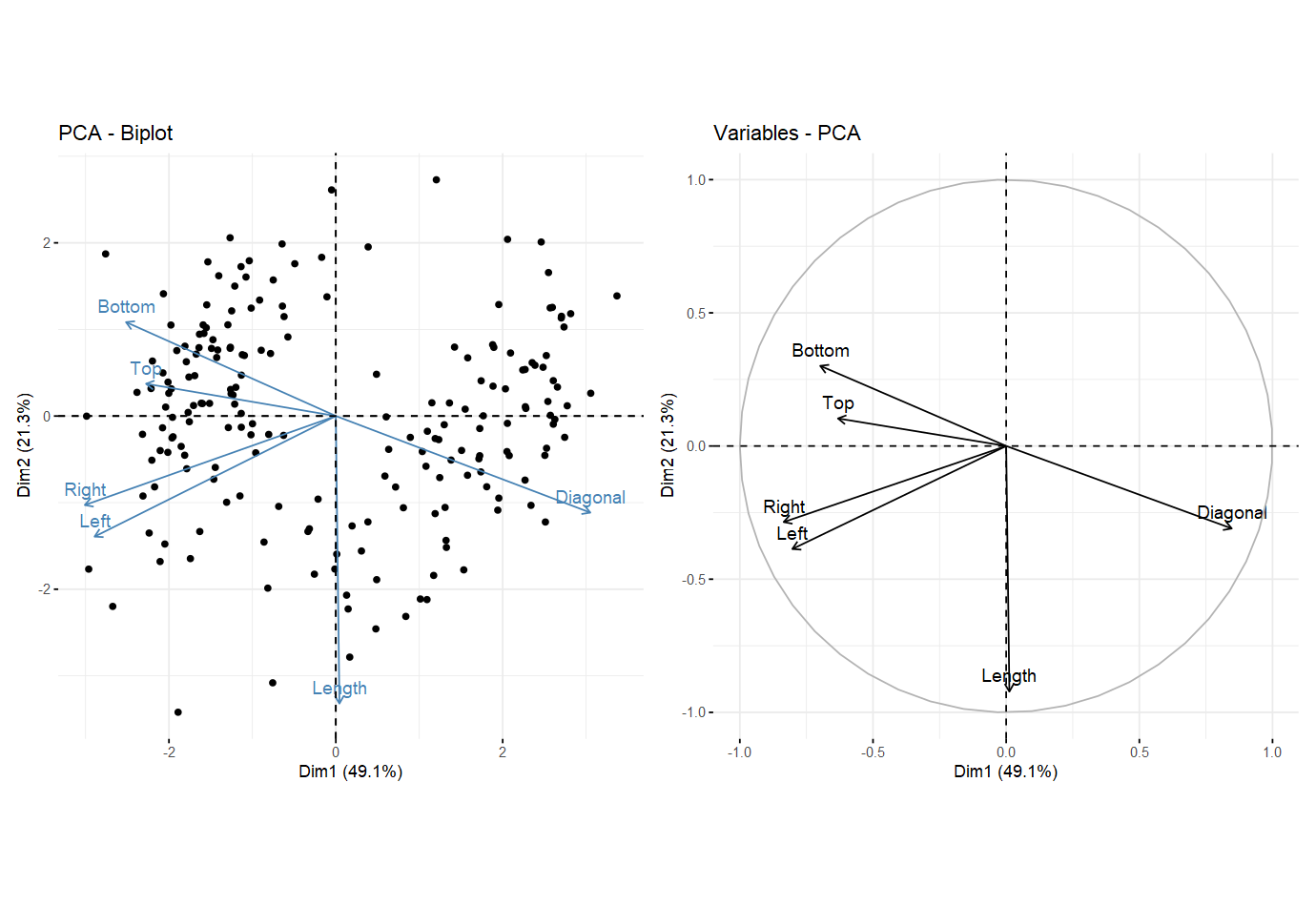
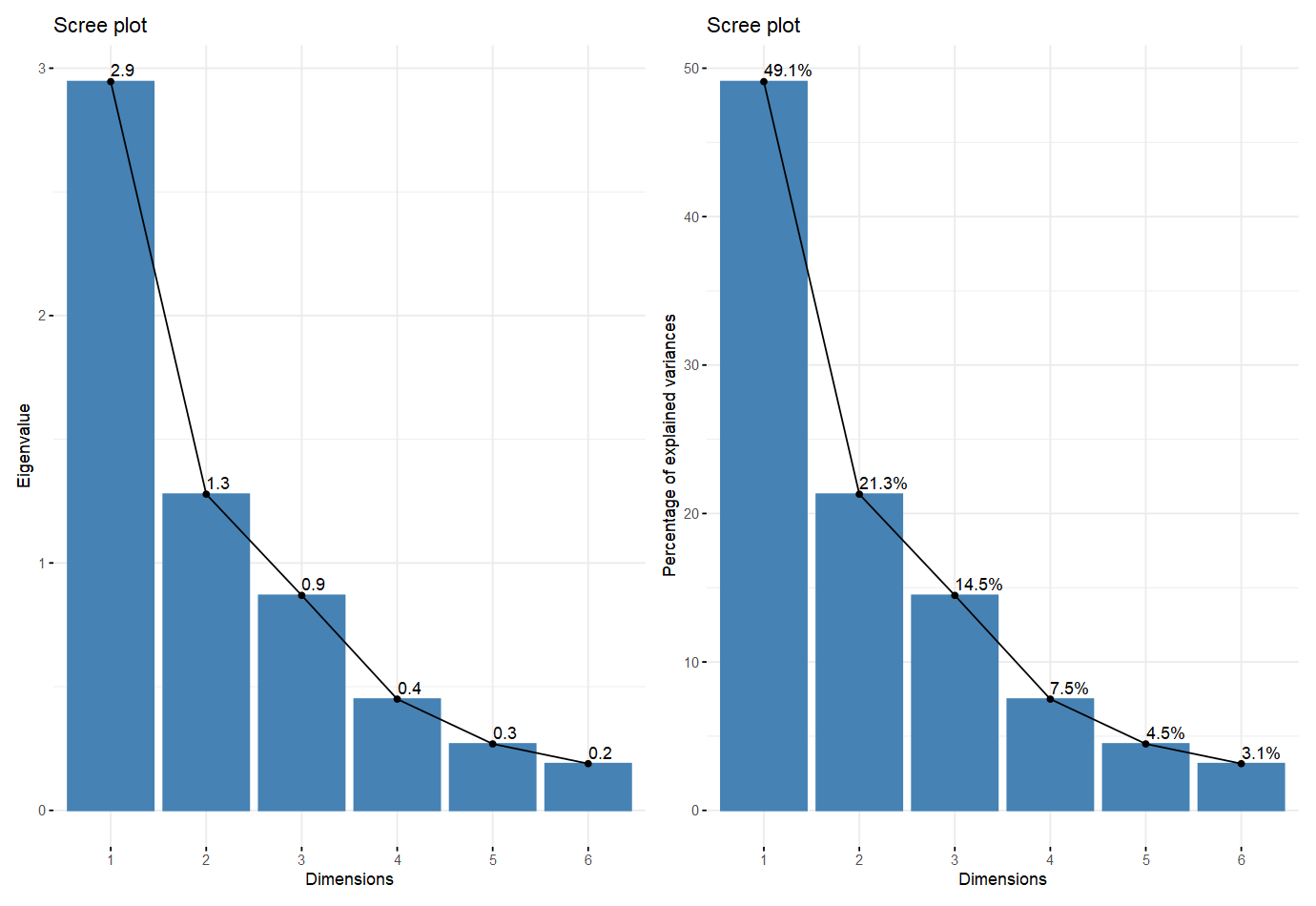
(2)主成分方差陡坡图#
- 又常成为elbow图,可用于辅助判断保留主成分的个数
1
2
3
|
p1 = fviz_screeplot(pca, addlabels = TRUE, choice = "eigenvalue")
p2 = fviz_screeplot(pca, addlabels = TRUE, choice = "variance")
p1 + p2
|
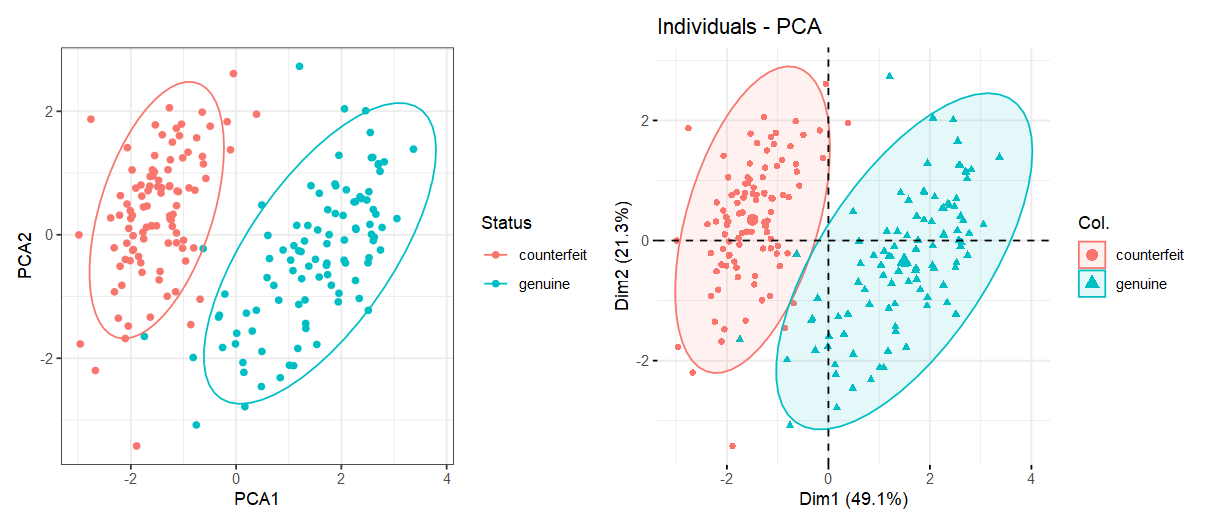
(3) 样本的主成分值分布图#
1
2
3
4
5
6
7
8
9
10
11
12
|
swissPca <- swissTib %>%
mutate(PCA1 = pca$x[, 1], PCA2 = pca$x[, 2])
p1 = ggplot(swissPca, aes(PCA1, PCA2, col = Status)) +
geom_point() +
stat_ellipse() +
theme_bw()
p2 = fviz_pca_ind(pca,
geom.ind = c("point"),
col.ind = swissTib$Status,
addEllipses = TRUE)
p1 + p2
|
2.4 预测新样本的主成分值#
1
2
3
4
5
6
7
8
9
10
11
12
13
|
newBanknotes <- tibble(
Length = c(214, 216),
Left = c(130, 128),
Right = c(132, 129),
Bottom = c(12, 7),
Top = c(12, 8),
Diagonal = c(138, 142)
)
newBanknotes
predict(pca, newBanknotes)
# PC1 PC2 PC3 PC4 PC5 PC6
# [1,] -4.729496 1.9989069 -0.1058105 -1.658777 -3.202514 1.623096
# [2,] 6.465758 -0.8918486 -0.8214539 3.468704 -1.837978 2.339436
|





