在建立通用线性模型时,当模型参数即斜率值绝对值过大时,容易存在过拟合的风险。可通过下面介绍的3种正则化方法将每个预测变量的斜率参数缩小为0或者接近0。
$$
y = \beta_0 + \beta_1x_1 + \beta_2x_2 + …+\beta_kx_k + \epsilon
$$
1、三种正则化方法#
线性回归最小二乘法损失函数:MSE
如下公式表示在一组给定的参数值模型中 所有预测值与观测值的差值的平方和(残差和,RSS):
$$
J = \sum_{i=1}^n(y_i-\hat{y_i})^2
$$
1.1 岭回归#
在上述RRS损失函数公式中,添加L2范数(所有斜率值的平方和)。可通过λ参数控制惩罚的强度。
$$
J=\sum_{i=1}^n(y_i-\hat{y_i})^2 + \lambda \sum_{j=1}^p{\beta_j^2}
$$
可结合下图理解:假设有两个预测变量,即有两个斜率参数。
(1)绿色圆表示不同参数值组合的MSE,中心值最小,越往外越大,黑色边表示相同MSE的等高线。
(2)蓝色圆边表示具有相同L2结果的不同参数值[r^2=β1^2+β2^2],总会存在一组参数值对应的RSS最小(如下图所示)。

1.2 LASSO回归#
在上述RSS损失函数公式中,添加L1范数(所有斜率值的绝对值和)。可通过λ参数控制惩罚的强度。
$$
J=\sum_{i=1}^n(y_i-\hat{y_i})^2 + \lambda \sum_{j=1}^p{|\beta_j|}
$$
可结合下图理解:假设有两个预测变量,即有两个斜率参数。
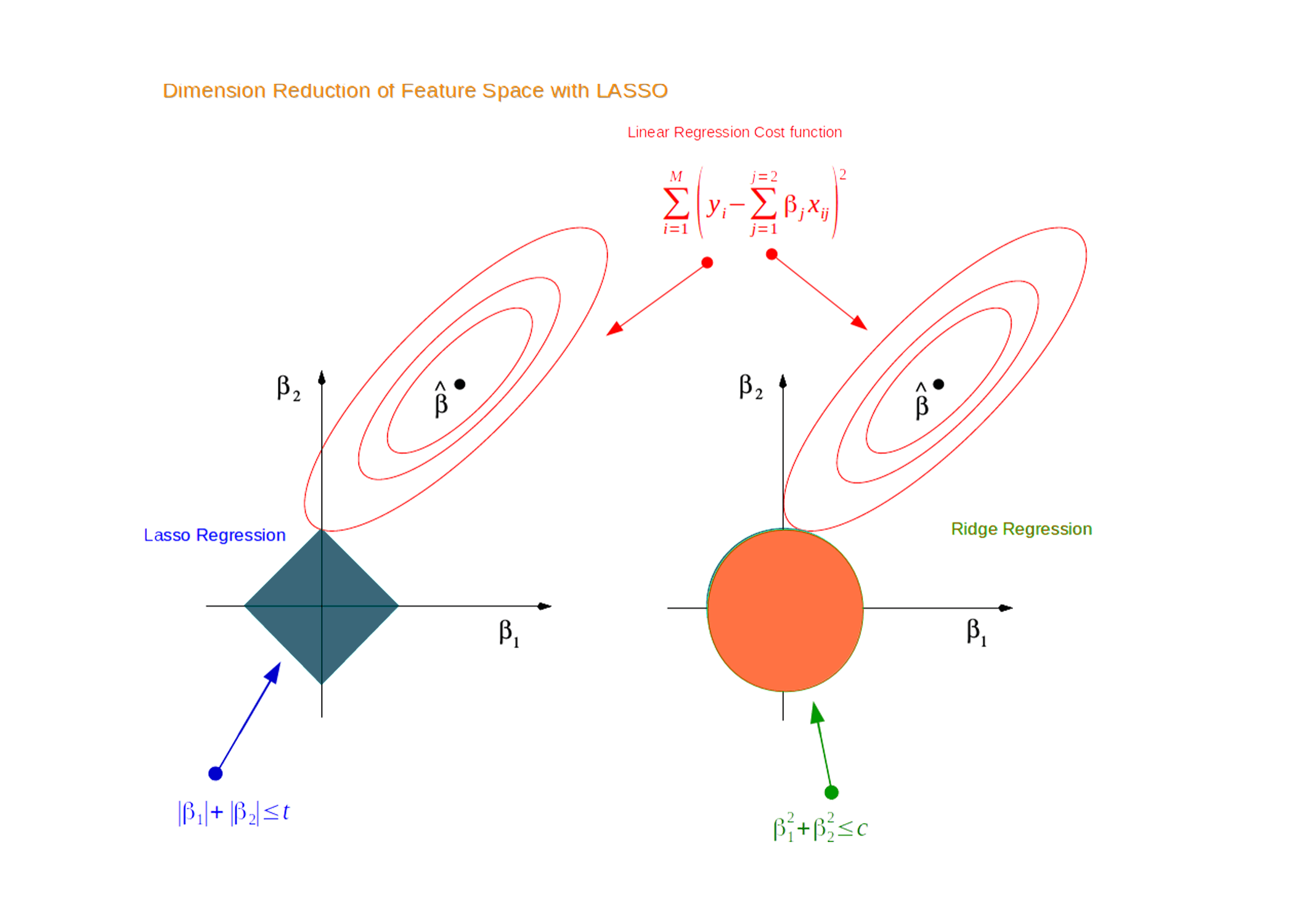
(1)红色同心圆表示不同参数值组合的MSE,中心值最小,越往外越大,黑色边表示相同MSE的等高线。
(2)蓝色正方形边表示具有相同L1结果的不同参数值[r=|β1|+|β2|],总会存在一组参数值对应的RSS最小(如下图所示)。

1.3 弹性网络#
(1) 岭回归与LASSO回归比较#
-
如上公式岭回归与LASSO回归的最主要差异在于惩罚项L2范数与L1范数的区别。
$$
J_{L2}=\sum_{i=1}^n(y_i-\hat{y_i})^2 + \lambda \sum_{j=1}^p{\beta_j^2}
$$
$$
J_{L1}=\sum_{i=1}^n(y_i-\hat{y_i})^2 + \lambda \sum_{j=1}^p{|\beta_j|}
$$
-
当λ=0时,等价于不加入惩罚项,取一组参数值使RRS值最小即可;
-
当λ>0时,岭回归加入了L2范数,LASSO回归加入了L1范数;虽然计算方式不同,但都与斜率值参数偏离0的程度呈正比。
-
当λ值不断增大时,惩罚项的权重不断增高;从而导致通过缩小斜率参数值使得损失函数总值下降的收益就越大。
- 换言之考虑惩罚项下降的强度与RRS项增高的强度,此时斜率参数值越接近0越好;
- 考虑到LASSO回归与岭回归形状的不同,LASSO能够将小的参数值缩小至0,即在模型中删除该变量,从而实现了特征选择的目的。
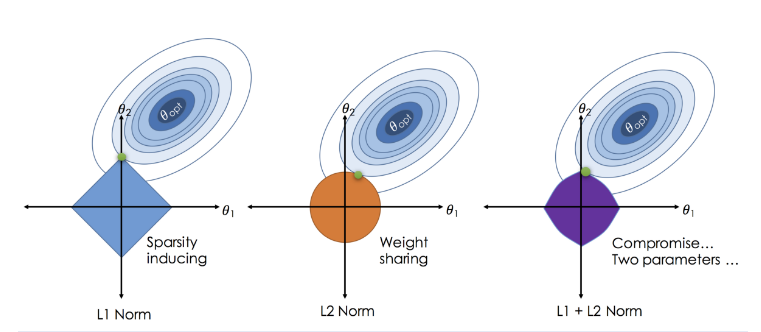
(2)弹性网络#
弹性网络中同时包含L2与L1正则化,通过α参数控制L2范数和L1范数的权重。所以在弹性网络中会有两个超参数。
如下公式
$$
J_{Net} = \sum_{i=1}^n(y_i-\hat{y_i})^2 + \lambda { (1-\alpha)\sum_{j=1}^p{\beta_j^2} + \alpha \sum_{j=1}^p{|\beta_j|} }
$$
2、mlr建模#
- 示例数据:小麦年产量
- 目的:根据第1~9列的预测变量信息预测小麦的产量
- 根据mlr包提供的"regr.glmnet"方法,进行三种正则化建模。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
library(mlr)
data(Iowa, package = "lasso2")
iowaTib <- Iowa
head(iowaTib)
# Year Rain0 Temp1 Rain1 Temp2 Rain2 Temp3 Rain3 Temp4 Yield
# 1 1930 17.75 60.2 5.83 69.0 1.49 77.9 2.42 74.4 34.0
# 2 1931 14.76 57.5 3.83 75.0 2.72 77.2 3.30 72.6 32.9
# 3 1932 27.99 62.3 5.17 72.0 3.12 75.8 7.10 72.2 43.0
# 4 1933 16.76 60.5 1.64 77.8 3.45 76.4 3.01 70.5 40.0
# 5 1934 11.36 69.5 3.49 77.2 3.85 79.7 2.84 73.4 23.0
# 6 1935 22.71 55.0 7.00 65.9 3.35 79.4 2.42 73.6 38.4
##第10列为小麦的产量
##其余列为小麦生长不同阶段的天气情况
iowaTask <- makeRegrTask(data = iowaTib, target = "Yield")
|
2.1 岭回归#
2.1.1 确定训练方法#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
##(1)定义学习器
ridge <- makeLearner("regr.glmnet", alpha = 0)
# getParamSet(ridge)
# 默认对数据进行标准化,以避免不同尺度的斜率参数的差异影响
##(2)定义超参数空间:s即为λ,控制惩罚项的权重
ridgeParamSpace <- makeParamSet(
makeNumericParam("s", lower = 0, upper = 15))
##(3)随机搜索200个超参数
randSearch <- makeTuneControlRandom(maxit = 200)
##(4)10次重复的3折交叉验证
cvForTuning <- makeResampleDesc("RepCV", folds = 3, reps = 10)
|
2.1.2 选取最优超参数#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
library(parallel)
library(parallelMap)
parallelStartSocket(cpus = detectCores())
tunedRidgePars <- tuneParams(ridge, task = iowaTask, # ~30 sec
resampling = cvForTuning,
par.set = ridgeParamSpace,
control = randSearch)
parallelStop()
#最优超参数结果
tunedRidgePars$x
#$s
#[1] 5.898183
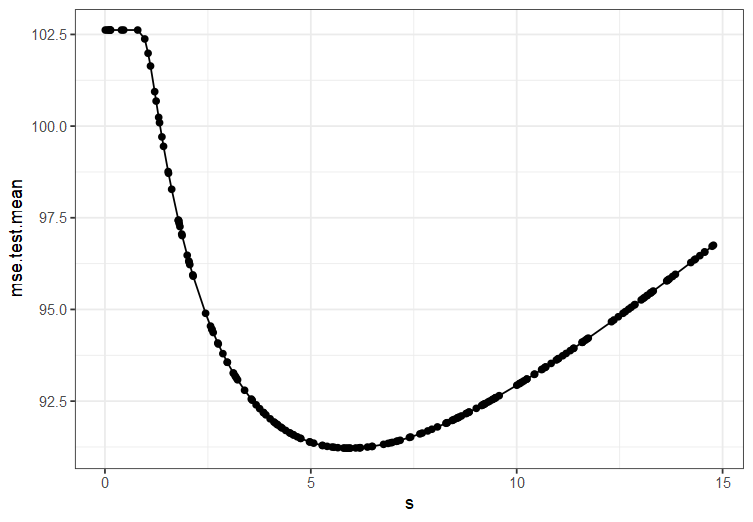
#不同超参数结果可视化
ridgeTuningData <- generateHyperParsEffectData(tunedRidgePars)
plotHyperParsEffect(ridgeTuningData, x = "s", y = "mse.test.mean",
plot.type = "line") +
theme_bw()
|
2.1.3 训练模型#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
##训练模型
tunedRidge <- setHyperPars(ridge, par.vals = tunedRidgePars$x)
tunedRidgeModel <- train(tunedRidge, iowaTask)
##查看模型结果
ridgeModelData <- getLearnerModel(tunedRidgeModel)
ridgeCoefs <- coef(ridgeModelData, s = tunedRidgePars$x$s)
ridgeCoefs
# 10 x 1 sparse Matrix of class "dgCMatrix"
# s1
# (Intercept) -916.65674179
# Year 0.53685059
# Rain0 0.34648992
# Temp1 -0.23854000
# Rain1 -0.70694968
# Temp2 0.03531768
# Rain2 1.92710185
# Temp3 -0.57686084
# Rain3 0.64050635
# Temp4 -0.47974939
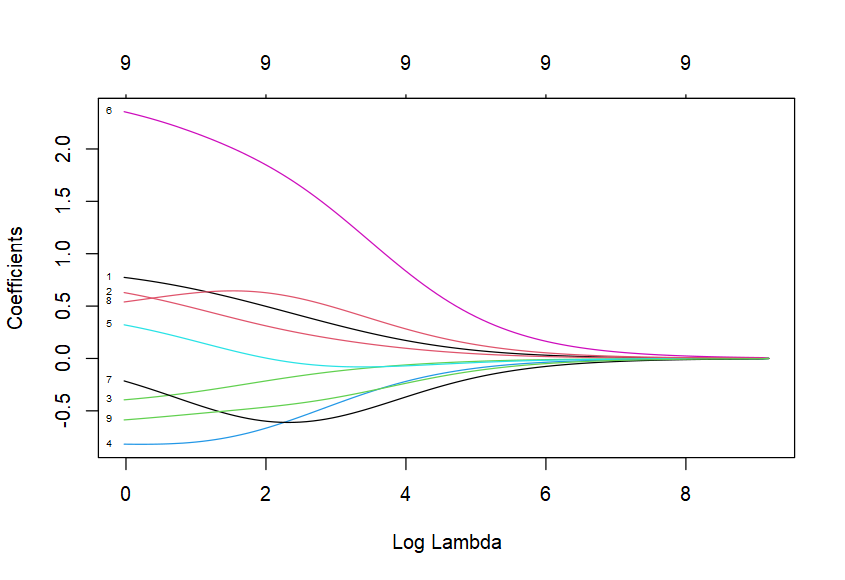
plot(ridgeModelData, xvar = "lambda", label = TRUE)
|
之前提及"regr.glmnet"会自动标准化,在计算斜率时则会自动转为变量原来的尺度。
2.2 lasso回归#
2.2.1 确定训练方法#
- 除了定义学习器时,alpha参数改为1,其它保持不变
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
##(1)定义学习器
lasso <- makeLearner("regr.glmnet", alpha = 1)
# getParamSet(lasso)
# 默认对数据进行标准化,以避免不同尺度的斜率参数的差异影响
##(2)定义超参数空间:s即为λ,控制惩罚项的权重
lassoParamSpace <- makeParamSet(
makeNumericParam("s", lower = 0, upper = 15))
##(3)随机搜索200个超参数
randSearch <- makeTuneControlRandom(maxit = 200)
##(4)10次重复的3折交叉验证
cvForTuning <- makeResampleDesc("RepCV", folds = 3, reps = 10)
|
2.2.2 选取最优超参数#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
library(parallel)
library(parallelMap)
parallelStartSocket(cpus = detectCores())
tunedLassoPars <- tuneParams(lasso, task = iowaTask, # ~30 sec
resampling = cvForTuning,
par.set = lassoParamSpace,
control = randSearch)
parallelStop()
#最优超参数结果
tunedLassoPars$x
#$s
#[1] 1.647296
#不同超参数结果可视化
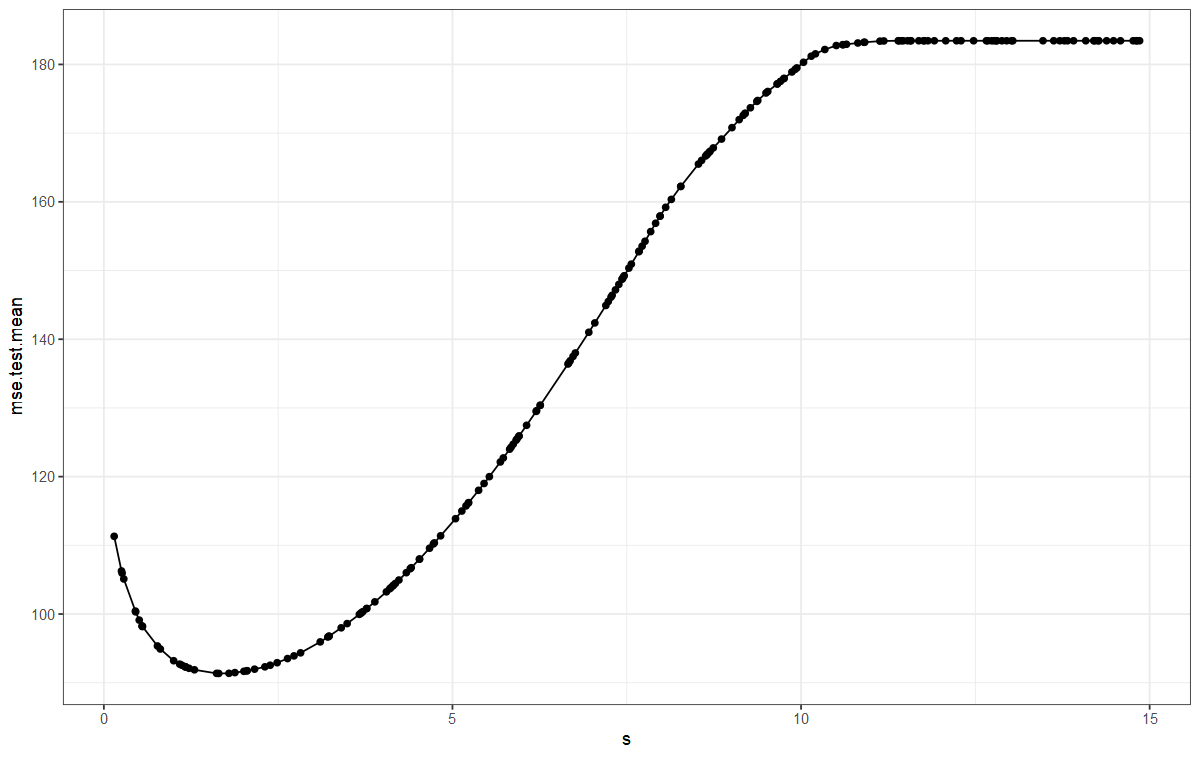
lassoTuningData <- generateHyperParsEffectData(tunedLassoPars)
plotHyperParsEffect(lassoTuningData, x = "s", y = "mse.test.mean",
plot.type = "line") +
theme_bw()
|
2.2.3 训练模型#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
##训练模型
tunedLasso <- setHyperPars(lasso, par.vals = tunedRidgePars$x)
tunedLassoModel <- train(tunedLasso, iowaTask)
##查看模型结果
lassoModelData <- getLearnerModel(tunedLassoModel)
lassoCoefs <- coef(lassoModelData, s = tunedLassoPars$x$s)
lassoCoefs
# 10 x 1 sparse Matrix of class "dgCMatrix"
# s1
# (Intercept) -1.313315e+03
# Year 7.138660e-01
# Rain0 1.489506e-01
# Temp1 .
# Rain1 .
# Temp2 .
# Rain2 1.890166e+00
# Temp3 -8.095605e-02
# Rain3 7.292344e-02
# Temp4 -4.042185e-01
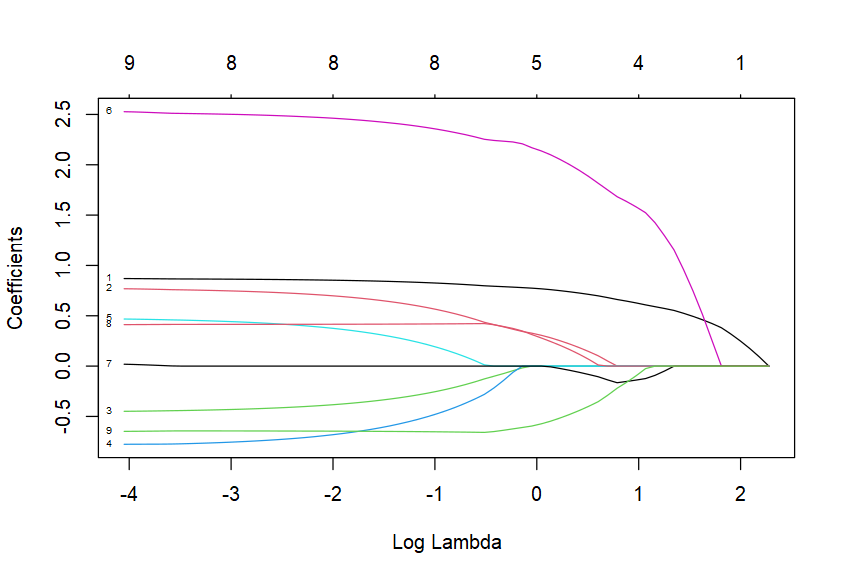
##如上有3个变量被剔除
plot(lassoModelData, xvar = "lambda", label = TRUE)
|
2.3 弹性网络#
2.3.1 确定训练方法#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
elastic <- makeLearner("regr.glmnet")
##(1)定义学习器
elastic <- makeLearner("regr.glmnet")
# getParamSet(elastic)
# 默认对数据进行标准化,以避免不同尺度的斜率参数的差异影响
##(2)定义超参数空间:s即为λ,控制惩罚项的权重
elasticParamSpace <- makeParamSet(
makeNumericParam("s", lower = 0, upper = 10),
makeNumericParam("alpha", lower = 0, upper = 1))
##(3)随机搜索400个超参数
randSearchElastic <- makeTuneControlRandom(maxit = 400)
##(4)10次重复的3折交叉验证
cvForTuning <- makeResampleDesc("RepCV", folds = 3, reps = 10)
|
2.3.2 选取最优超参数组合#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
library(parallel)
library(parallelMap)
parallelStartSocket(cpus = detectCores())
tunedElasticPars <- tuneParams(elastic, task = iowaTask, # ~30 sec
resampling = cvForTuning,
par.set = elasticParamSpace,
control = randSearchElastic)
parallelStop()
#最优超参数结果
tunedElasticPars$x
#$s
#[1] 1.786091
#$alpha
#[1] 0.8142816
#不同超参数结果可视化
elasticTuningData <- generateHyperParsEffectData(tunedElasticPars)
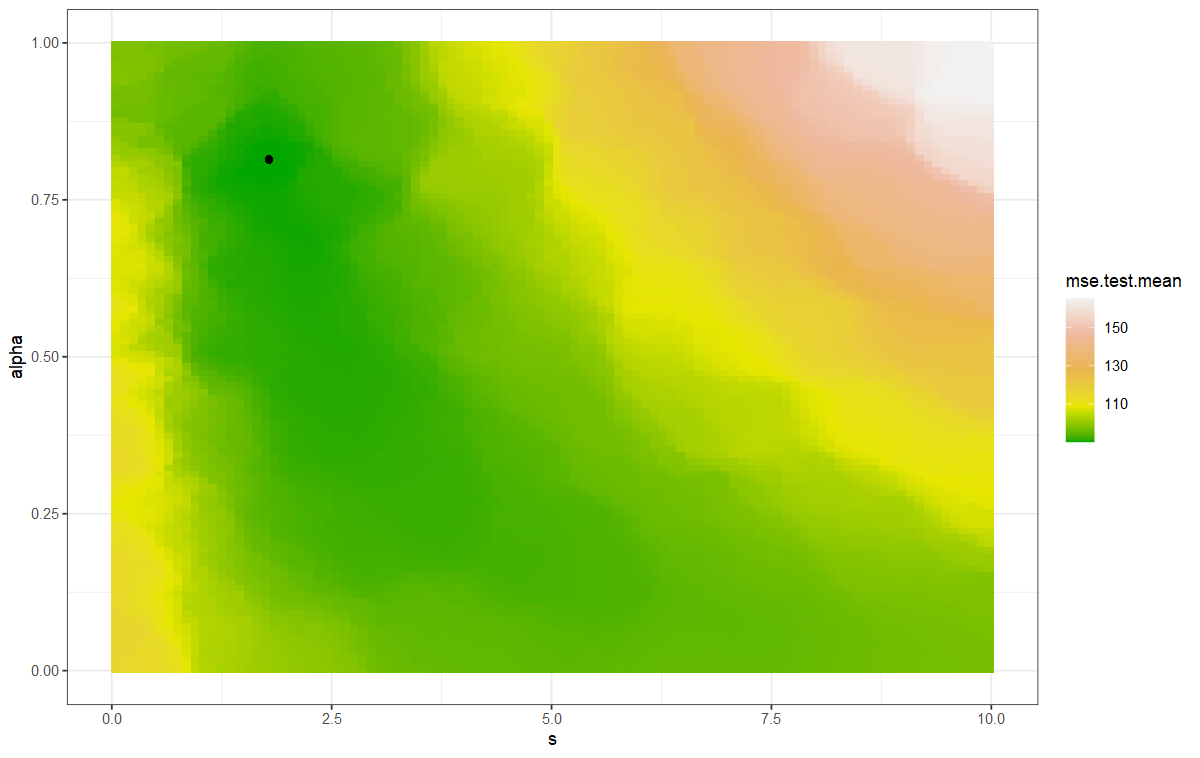
plotHyperParsEffect(elasticTuningData, x = "s", y = "alpha",
z = "mse.test.mean", interpolate = "regr.kknn",
plot.type = "heatmap") +
scale_fill_gradientn(colours = terrain.colors(5)) +
geom_point(x = tunedElasticPars$x$s, y = tunedElasticPars$x$alpha) +
theme_bw()\
#如下图,黑点标注的即为最优超参数组合
|
2.3.3 训练模型#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
##训练模型
tunedElastic <- setHyperPars(elastic, par.vals = tunedElasticPars$x)
tunedElasticModel <- train(tunedElastic, iowaTask)
##查看模型结果
elasticModelData <- getLearnerModel(tunedElasticModel)
elasticCoefs <- coef(elasticModelData, s = tunedElasticPars$x$s)
elasticCoefs
# 10 x 1 sparse Matrix of class "dgCMatrix"
# s1
# (Intercept) -1290.1150312
# Year 0.7038625
# Rain0 0.1786434
# Temp1 .
# Rain1 .
# Temp2 .
# Rain2 1.9443047
# Temp3 -0.1234248
# Rain3 0.1621764
# Temp4 -0.4266126
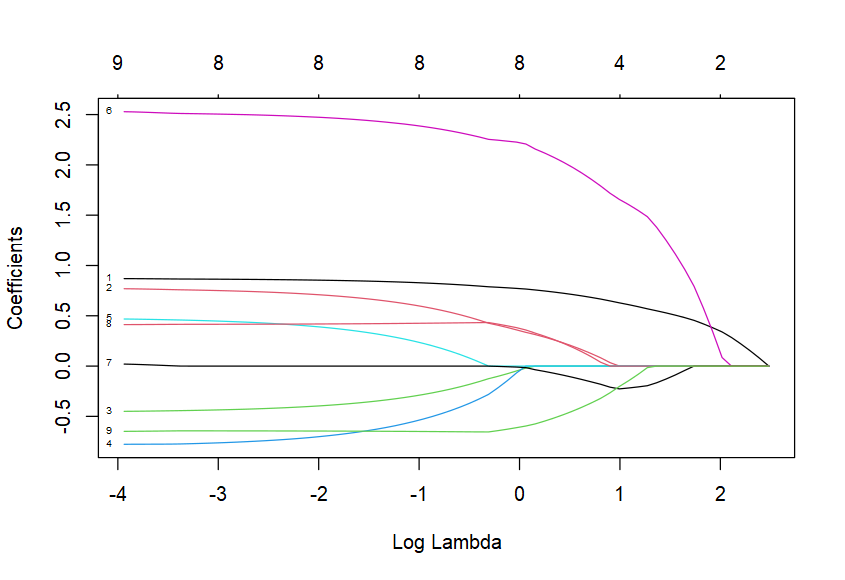
##如上同样有3个变量被剔除
plot(elasticModelData, xvar = "lambda", label = TRUE)
|
2.4 对比三个模型结果#
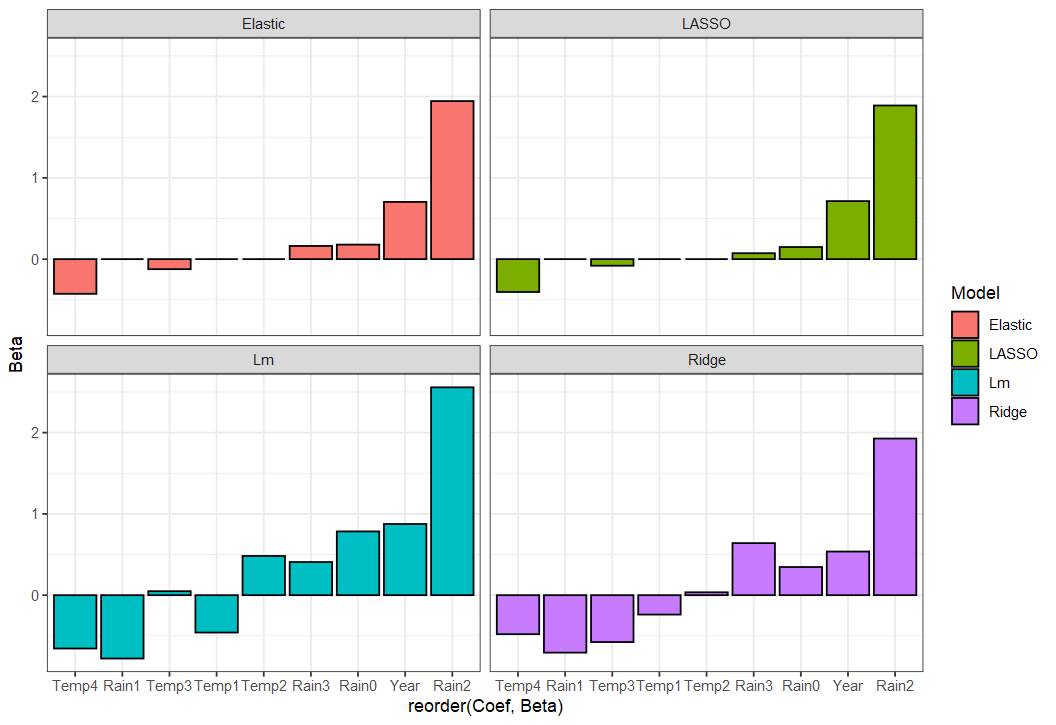
2.4.1 预测变量系数比较#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
#(1)普通线性回归
lmCoefs <- coef(lm(Yield ~ ., data = iowaTib))
#(2)岭回归
coefTib <- tibble(Coef = rownames(ridgeCoefs)[-1],
Ridge = as.vector(ridgeCoefs)[-1],
Lm = as.vector(lmCoefs)[-1])
coefUntidy <- gather(coefTib, key = Model, value = Beta, -Coef)
#(3)lasso回归
coefTib$LASSO <- as.vector(lassoCoefs)[-1]
coefUntidy <- gather(coefTib, key = Model, value = Beta, -Coef)
#(4)弹性网络
coefTib$Elastic <- as.vector(elasticCoefs)[-1]
coefUntidy <- gather(coefTib, key = Model, value = Beta, -Coef)
ggplot(coefUntidy, aes(reorder(Coef, Beta), Beta, fill = Model)) +
geom_bar(stat = "identity", position = "dodge", col = "black") +
facet_wrap(~ Model) +
theme_bw()
|
2.4.2 benchmark#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
##(1)初始化模型
ridge <- makeLearner("regr.glmnet", alpha = 0, id="ridge")
ridgeWrapper <- makeTuneWrapper(ridge, resampling = cvForTuning,
par.set = ridgeParamSpace,
control = randSearch)
lasso <- makeLearner("regr.glmnet", alpha = 0, id="lasso")
lassoWrapper <- makeTuneWrapper(lasso, resampling = cvForTuning,
par.set = lassoParamSpace,
control = randSearch)
elastic <- makeLearner("regr.glmnet", alpha = 0, id="elastic")
elasticWrapper <- makeTuneWrapper(elastic, resampling = cvForTuning,
par.set = elasticParamSpace,
control = randSearchElastic)
learners = list(ridgeWrapper, lassoWrapper, elasticWrapper, "regr.lm")
##(2)开始测试
library(parallel)
library(parallelMap)
kFold3 <- makeResampleDesc("CV", iters = 3)
parallelStartSocket(cpus = detectCores())
bench <- benchmark(learners, iowaTask, kFold3)
parallelStop()
bench
# bench
# task.id learner.id mse.test.mean
# 1 iowaTib ridge.tuned 204.6557
# 2 iowaTib lasso.tuned 209.6984
# 3 iowaTib elastic.tuned 179.3852
# 4 iowaTib regr.lm 251.6789
|










