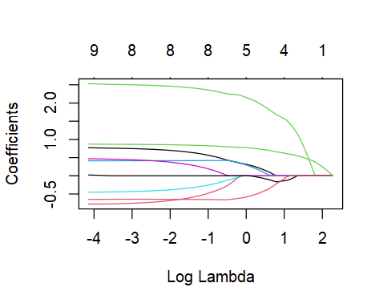
在建立通用线性模型时,当模型参数即斜率值绝对值过大时,容易存在过拟合的风险。可通过下面介绍的3种正则化方法将每个预测变量的斜率参数缩小为0或者接近0。
$$
y = \beta_0 + \beta_1x_1 + \beta_2x_2 + …+\beta_kx_k + \epsilon
$$
1、三种正则化方法#
线性回归最小二乘法损失函数:MSE
如下公式表示在一组给定的参数值模型中 所有预测值与观测值的差值的平方和(残差和,RSS):
$$
J = \sum_{i=1}^n(y_i-\hat{y_i})^2
$$
1.1 岭回归#
在上述RRS损失函数公式中,添加L2范数(所有斜率值的平方和)。可通过λ参数控制惩罚的强度。
$$
J=\sum_{i=1}^n(y_i-\hat{y_i})^2 + \lambda \sum_{j=1}^p{\beta_j^2}
$$
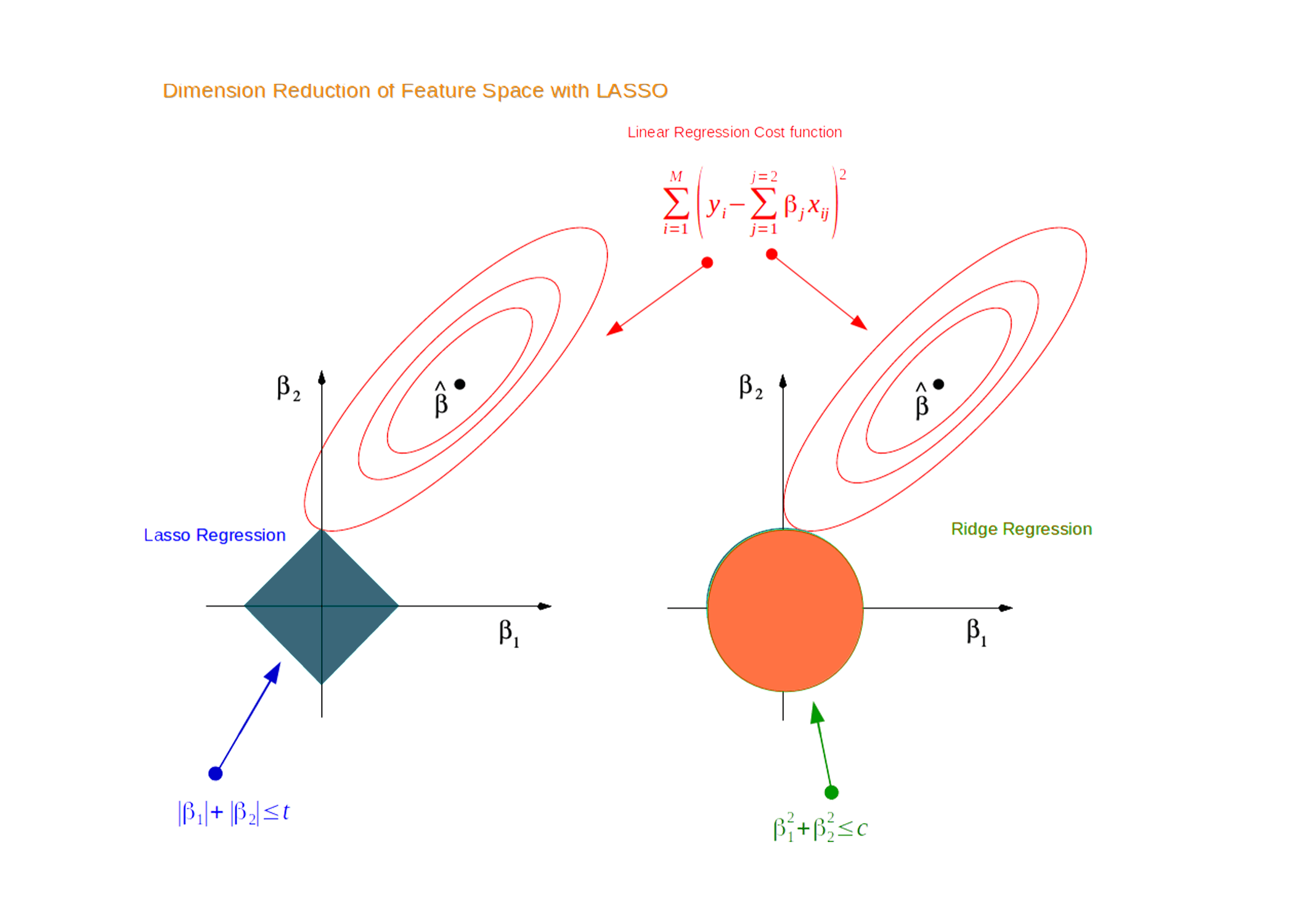
可结合下图理解:假设有两个预测变量,即有两个斜率参数。
(1)绿色圆表示不同参数值组合的MSE,中心值最小,越往外越大,黑色边表示相同MSE的等高线。
(2)蓝色圆边表示具有相同L2结果的不同参数值[r^2=β1^2+β2^2],总会存在一组参数值对应的RSS最小(如下图所示)。

1.2 LASSO回归#
在上述RSS损失函数公式中,添加L1范数(所有斜率值的绝对值和)。可通过λ参数控制惩罚的强度。
$$
J=\sum_{i=1}^n(y_i-\hat{y_i})^2 + \lambda \sum_{j=1}^p{|\beta_j|}
$$
可结合下图理解:假设有两个预测变量,即有两个斜率参数。
(1)红色同心圆表示不同参数值组合的MSE,中心值最小,越往外越大,黑色边表示相同MSE的等高线。
(2)蓝色正方形边表示具有相同L1结果的不同参数值[r=|β1|+|β2|],总会存在一组参数值对应的RSS最小(如下图所示)。

1.3 弹性网络#
(1) 岭回归与LASSO回归比较#
-
如上公式岭回归与LASSO回归的最主要差异在于惩罚项L2范数与L1范数的区别。
$$
J_{L2}=\sum_{i=1}^n(y_i-\hat{y_i})^2 + \lambda \sum_{j=1}^p{\beta_j^2}
$$
$$
J_{L1}=\sum_{i=1}^n(y_i-\hat{y_i})^2 + \lambda \sum_{j=1}^p{|\beta_j|}
$$
-
当λ=0时,等价于不加入惩罚项,取一组参数值使RRS值最小即可;
-
当λ>0时,岭回归加入了L2范数,LASSO回归加入了L1范数;虽然计算方式不同,但都与斜率值参数偏离0的程度呈正比。
-
当λ值不断增大时,惩罚项的权重不断增高;从而导致通过缩小斜率参数值使得损失函数总值下降的收益就越大。
- 换言之考虑惩罚项下降的强度与RRS项增高的强度,此时斜率参数值越接近0越好;
- 考虑到LASSO回归与岭回归形状的不同,LASSO能够将小的参数值缩小至0,即在模型中删除该变量,从而实现了特征选择的目的。
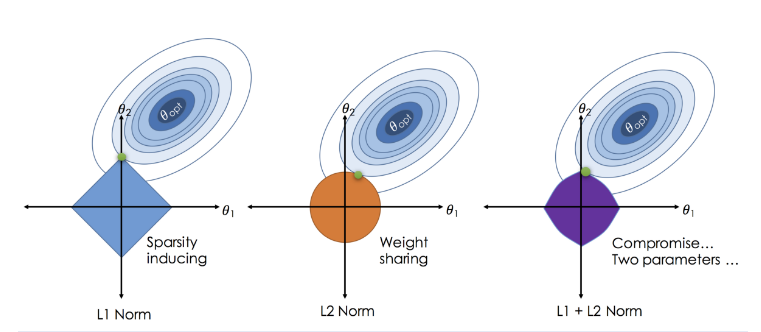
(2)弹性网络#
弹性网络中同时包含L2与L1正则化,通过α参数控制L2范数和L1范数的权重。所以在弹性网络中会有两个超参数。
如下公式
$$
J_{Net} = \sum_{i=1}^n(y_i-\hat{y_i})^2 + \lambda { (1-\alpha)\sum_{j=1}^p{\beta_j^2} + \alpha \sum_{j=1}^p{|\beta_j|} }
$$
2、mlr建模#
- 示例数据:小麦年产量
- 目的:根据第1~9列的预测变量信息预测小麦的产量
- 根据mlr包提供的"regr.glmnet"方法,进行三种正则化建模。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
library(mlr3verse)
library(tidyverse)
data(Iowa, package = "lasso2")
head(Iowa)
# Year Rain0 Temp1 Rain1 Temp2 Rain2 Temp3 Rain3 Temp4 Yield
# 1 1930 17.75 60.2 5.83 69.0 1.49 77.9 2.42 74.4 34.0
# 2 1931 14.76 57.5 3.83 75.0 2.72 77.2 3.30 72.6 32.9
# 3 1932 27.99 62.3 5.17 72.0 3.12 75.8 7.10 72.2 43.0
# 4 1933 16.76 60.5 1.64 77.8 3.45 76.4 3.01 70.5 40.0
# 5 1934 11.36 69.5 3.49 77.2 3.85 79.7 2.84 73.4 23.0
# 6 1935 22.71 55.0 7.00 65.9 3.35 79.4 2.42 73.6 38.4
##第10列为小麦的产量
##其余列为小麦生长不同阶段的天气情况
task_regr = as_task_regr(Iowa, target = "Yield")
|
2.1 岭回归#
2.1.1 确定训练方法#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
##(1)定义学习器
learner = lrn("regr.glmnet")
learner$param_set
learner$param_set$values$alpha = 0
# getParamSet(ridge)
# 默认对数据进行标准化,以避免不同尺度的斜率参数的差异影响
##(2)定义超参数空间:s即为λ,控制惩罚项的权重
search_space = ps(
s = p_dbl(lower = 0, upper = 20)
)
design = data.frame(s = seq(0, 20, 0.5)) %>% as.data.table()
##(3)交叉验证/评价指标
resampling = rsmp("cv")
measure = msr("regr.mse")
|
2.1.2 选取最优超参数#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
instance = TuningInstanceSingleCrit$new(
task = task_regr,
learner = learner,
resampling = resampling,
measure = measure,
terminator = trm("none"),
search_space = search_space
)
tuner = tnr("design_points", design = design)
future::plan("multisession")
tuner$optimize(instance)
#历史记录
as.data.table(instance$archive)[,1:2] %>% head()
# s regr.mse
# 1: 0.0 112.04095
# 2: 0.5 112.04095
# 3: 1.0 112.15121
# 4: 1.5 106.14823
# 5: 2.0 101.21156
# 6: 2.5 97.64488
#最优超参数结果
instance$result_learner_param_vals
# $family
# [1] "gaussian"
# $alpha
# [1] 0
# $s
# [1] 4
instance$result_y
#regr.mse
#93.12861
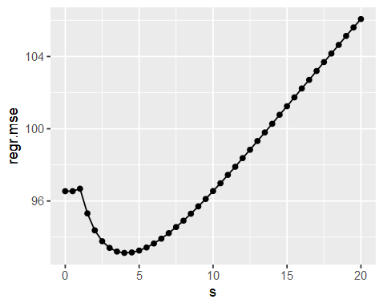
#可视化
as.data.table(instance$archive)[,1:2] %>%
ggplot(aes(x = s, y = regr.mse)) +
geom_line() +
geom_point()
|
2.1.3 训练模型#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
##训练模型
learner$param_set$values = instance$result_learner_param_vals
learner$train(task_regr)
##查看模型结果
learner$model
coef(learner$model, s = learner$param_set$values$s)
# 10 x 1 sparse Matrix of class "dgCMatrix"
# s1
# (Intercept) -1.047533e+03
# Rain0 4.109633e-01
# Rain1 -7.624006e-01
# Rain2 2.046984e+00
# Rain3 6.438645e-01
# Temp1 -2.795682e-01
# Temp2 9.716923e-02
# Temp3 -5.171002e-01
# Temp4 -5.040869e-01
# Year 6.010389e-01
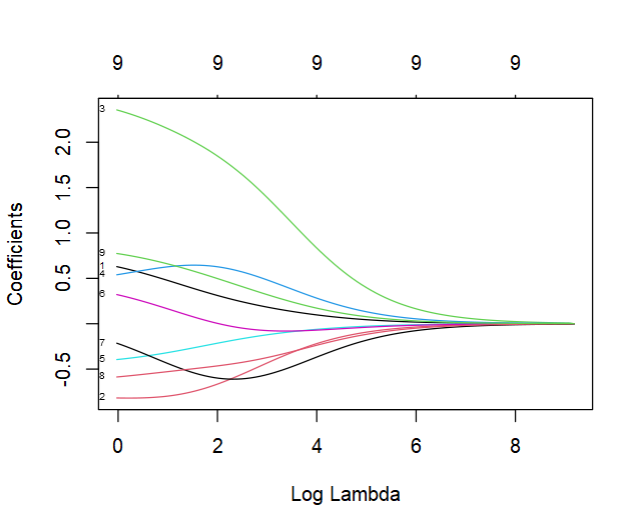
plot(learner$model, xvar = "lambda", label = TRUE)
|
之前提及"regr.glmnet"会自动标准化,在计算斜率时则会自动转为变量原来的尺度。
2.2 lasso回归#
2.2.1 确定训练方法#
- 除了定义学习器时,alpha参数改为1,其它保持不变
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
##(1)定义学习器
learner = lrn("regr.glmnet")
learner$param_set
learner$param_set$values$alpha = 1
# getParamSet(ridge)
# 默认对数据进行标准化,以避免不同尺度的斜率参数的差异影响
##(2)定义超参数空间:s即为λ,控制惩罚项的权重
search_space = ps(
s = p_dbl(lower = 0, upper = 20)
)
design = data.frame(s = seq(0, 20, 0.5)) %>% as.data.table()
##(3)交叉验证/评价指标
resampling = rsmp("cv")
measure = msr("regr.mse")
|
2.2.2 选取最优超参数#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
instance = TuningInstanceSingleCrit$new(
task = task_regr,
learner = learner,
resampling = resampling,
measure = measure,
terminator = trm("none"),
search_space = search_space
)
tuner = tnr("design_points", design = design)
future::plan("multisession")
tuner$optimize(instance)
#历史记录
as.data.table(instance$archive)[,1:2] %>% head()
# s regr.mse
# 1: 0.0 114.64266
# 2: 0.5 89.90857
# 3: 1.0 81.79360
# 4: 1.5 81.73846
# 5: 2.0 86.30311
# 6: 2.5 89.77685
#最优超参数结果
instance$result_learner_param_vals
# $family
# [1] "gaussian"
# $alpha
# [1] 1
# $s
# [1] 1
instance$result_y
#regr.mse
#81.56699
#可视化
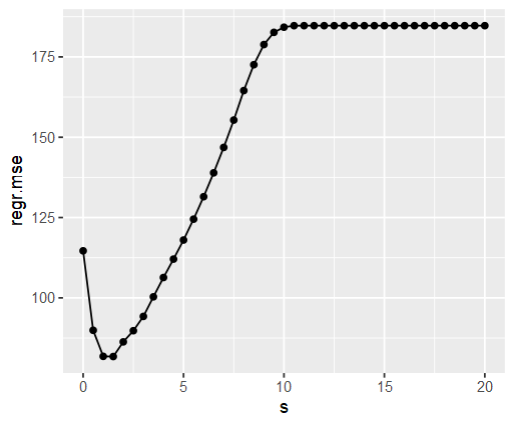
as.data.table(instance$archive)[,1:2] %>%
ggplot(aes(x = s, y = regr.mse)) +
geom_line() +
geom_point()
|
2.2.3 训练模型#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
##训练模型
learner$param_set$values = instance$result_learner_param_vals
learner$train(task_regr)
##查看模型结果
learner$model
coef(learner$model, s = learner$param_set$values$s)
# 10 x 1 sparse Matrix of class "dgCMatrix"
# s1
# (Intercept) -1421.9762963
# Rain0 0.3161326
# Rain1 .
# Rain2 2.1528392
# Rain3 0.2956521
# Temp1 .
# Temp2 .
# Temp3 .
# Temp4 -0.5843153
# Year 0.7707991
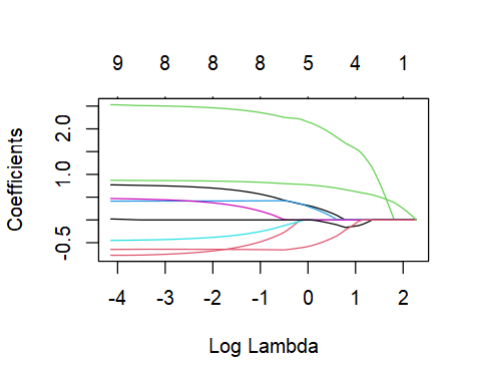
plot(learner$model, xvar = "lambda", label = TRUE)
|
2.3 弹性网络#
2.3.1 确定训练方法#
1
2
3
4
5
6
7
8
9
10
11
12
13
|
##(1)定义学习器
learner = lrn("regr.glmnet")
learner$param_set
#与上面两个不同的是,有两个超参数需要调节
search_space = ps(
s = p_dbl(lower = 0, upper = 20),
alpha = p_dbl(lower = 0, upper = 1)
)
design = expand.grid(alpha = seq(0, 1, 0.2),
s = seq(0, 20, 0.5)) %>% as.data.table()
resampling = rsmp("cv")
measure = msr("regr.mse")
|
2.3.2 选取最优超参数组合#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
|
instance = TuningInstanceSingleCrit$new(
task = task_regr,
learner = learner,
resampling = resampling,
measure = measure,
terminator = trm("none"),
search_space = search_space
)
tuner = tnr("design_points", design = design)
future::plan("multisession")
tuner$optimize(instance)
as.data.table(instance$archive)[,1:3] %>% head()
# s alpha regr.mse
# 1: 0 0.0 92.62672
# 2: 0 0.2 97.45767
# 3: 0 0.4 97.34487
# 4: 0 0.6 97.28724
# 5: 0 0.8 97.24310
# 6: 0 1.0 97.24670
instance$result_learner_param_vals
# $family
# [1] "gaussian"
# $s
# [1] 1
# $alpha
# [1] 1
instance$result_y
#regr.mse
#89.67037
|
2.3.3 训练模型#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
##训练模型
learner$param_set$values = instance$result_learner_param_vals
learner$train(task_regr)
##查看模型结果
learner$model
coef(learner$model, s = learner$param_set$values$s)
# 10 x 1 sparse Matrix of class "dgCMatrix"
# s1
# (Intercept) -1421.9762963
# Rain0 0.3161326
# Rain1 .
# Rain2 2.1528392
# Rain3 0.2956521
# Temp1 .
# Temp2 .
# Temp3 .
# Temp4 -0.5843153
# Year 0.7707991
plot(learner$model, xvar = "lambda", label = TRUE)
|