1、关于线性回归#
1.1 公式理解#
由于实际问题很少遇到单变量线性回归,所以更常见的表示为通用线性模型:
$$
y = \beta_0 + \beta_1x_1 + \beta_2x_2 + …+\beta_kx_k + \epsilon
$$
(1)β0表示截距,即所有预测变量取0时的值;
(2)β1等表示斜率,在其它预测变量不变时,每个预测变量每变动一个单位时输出变量的变化值。
(3)ε表示模型的未知误差,可以理解为残差。
如上公式,线性回归常用普通最小二乘法(OLS)寻找最佳的截距与斜率值的组合,最小化残差(预测值与真实值的差异)平方和。
对于分类变量(k类),会选择1类作为参考水平,同时生成(k-1)个虚拟变量,进而得到(k-1)个斜率值。此时的斜率值表示,该类的预测变量结果相对于参考水平的变化倍数。
1.2 注意点#
(1)线性回归的优势在于模型的可解释性(相对于随机森林、SVM等黑匣子)。即每个预测变量都有斜率值以表示对预测变量的影响;并且不同预测变量的影响是累加的。
(2)对于线性回归结果需要检查拟合值与真实值的残差是否满足两个条件。
- 正态分布:残差值是否符合以0为均值的正态分布。
- 同方差:输出变量的方差不会随着预测拟合值的变化而变化,如下图a的结果是符合的。
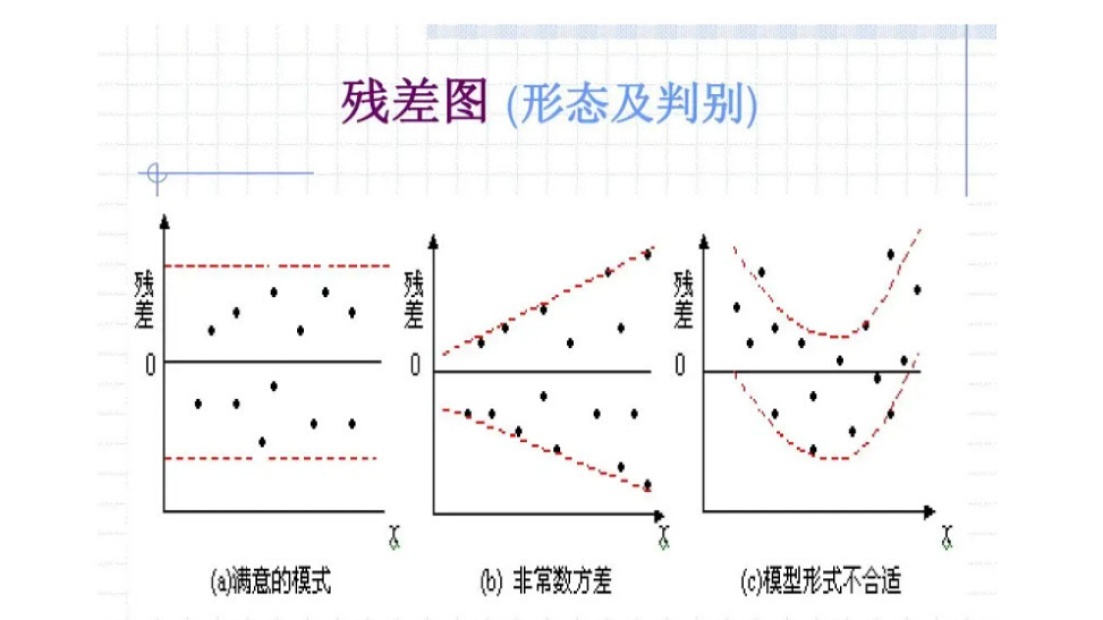
如果不满足上面两个条件,提示可能不适合使用通用线性回归,使得模型性能降低,可以尝试之后会学习的通用线性模型。
(3)对于回归问题的性能度量指标
- 平均绝对误差MAE:残差绝对值的均值;
- 均方误差MSE:残差平方和的均值;
- 均方根误差RMSE:MSE的平方根。
2、mlr建模#
1
2
|
library(mlr3verse)
library(tidyverse)
|
2.1 臭氧水平空气质量数据#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
data(Ozone, package = "mlbench")
colnames(Ozone) = c("Month", "Date", "Day", "Ozone", "Press_height",
"Wind", "Humid", "Temp_Sand", "Temp_Monte",
"Inv_height", "Press_grad", "Inv_temp", "Visib")
Ozone2 = Ozone %>%
dplyr::mutate(across(where(is.factor), as.numeric)) %>%
na.omit()
str(Ozone2)
# 'data.frame': 203 obs. of 13 variables:
# $ Month : num 1 1 1 1 1 1 1 1 1 1 ...
# $ Date : num 5 6 7 8 9 12 13 14 15 16 ...
# $ Day : num 1 2 3 4 5 1 2 3 4 5 ...
# $ Ozone : num 5 6 4 4 6 6 5 4 4 7 ...
# $ Press_height: num 5760 5720 5790 5790 5700 5720 5760 5780 5830 5870 ...
# $ Wind : num 3 4 6 3 3 3 6 6 3 2 ...
# $ Humid : num 51 69 19 25 73 44 33 19 19 19 ...
# $ Temp_Sand : num 54 35 45 55 41 51 51 54 58 61 ...
# $ Temp_Monte : num 45.3 49.6 46.4 52.7 48 ...
# $ Inv_height : num 1450 1568 2631 554 2083 ...
# $ Press_grad : num 25 15 -33 -28 23 9 -44 -44 -53 -67 ...
# $ Inv_temp : num 57 53.8 54.1 64.8 52.5 ...
# $ Visib : num 60 60 100 250 120 150 40 200 250 200 ...
# - attr(*, "na.action")= 'omit' Named int [1:163] 1 2 3 4 10 11 17 18 20 24 ...
# ..- attr(*, "names")= chr [1:163] "1" "2" "3" "4" ...
|
2.2 确定预测目标与训练方法#
1
2
3
4
5
|
##(1)确定预测目标:根据每天的空气相关记录数据,预测那一天的臭氧水平
task_regr = as_task_regr(Ozone2, target = "Ozone")
##(2)使用线性回归模型
learner = lrn("regr.lm")
|
2.3 特征筛选建模#
这一步是去除不具备预测价值的干扰变量,提高模型精度。有如下两种思路:
2.3.1 TopK个预测变量#
这种思路是评价每一个预测变量与待拟合变量的"关系",有很多评价指标。
1
2
3
4
5
6
|
ALL_mlr_filter = as.data.table(mlr_filters)
mlr_filters$keys()
# [1] "anova" "auc" "carscore" "cmim" "correlation"
# [6] "disr" "find_correlation" "importance" "information_gain" "jmi"
# [11] "jmim" "kruskal_test" "mim" "mrmr" "njmim"
# [16] "performance" "permutation" "relief" "selected_features" "variance"
|
然后根据指标结果,选取最有价值的若干个预测变量。具体的数量,可设置为超参数,选取最优的。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
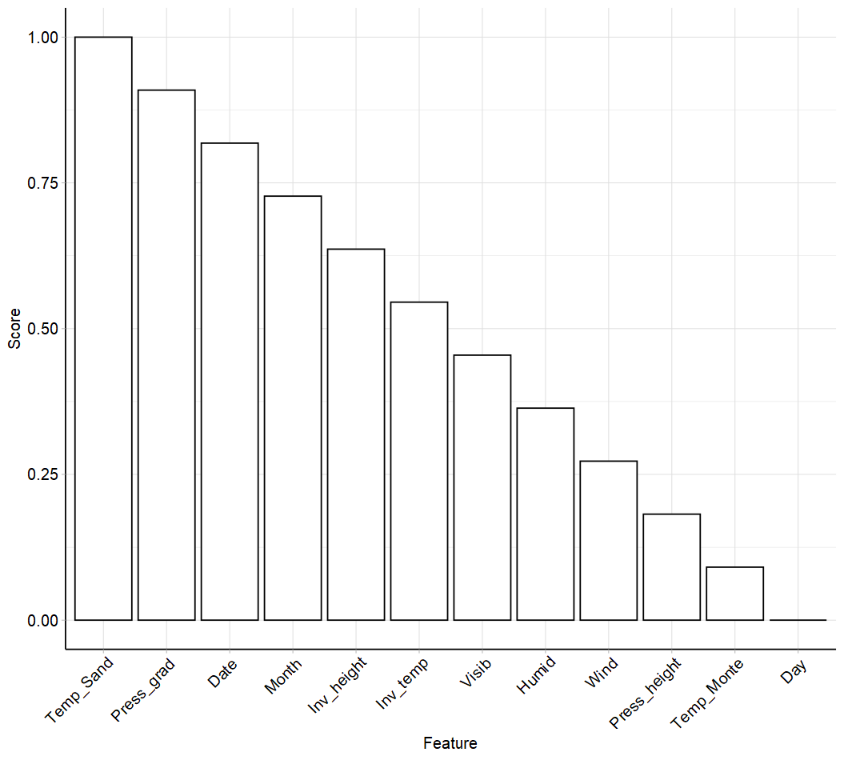
##(1)计算每个预测变量与待预测变量的关系指标
filter = flt("jmim")
filter$param_set$values
filter$calculate(task_regr)
as.data.table(filter)
# feature score
# 1: Temp_Sand 1.00000000
# 2: Press_grad 0.90909091
# 3: Date 0.81818182
# 4: Month 0.72727273
# 5: Inv_height 0.63636364
# 6: Inv_temp 0.54545455
# 7: Visib 0.45454545
# 8: Humid 0.36363636
# 9: Wind 0.27272727
# 10: Press_height 0.18181818
# 11: Temp_Monte 0.09090909
# 12: Day 0.00000000
|
2.3.2 遍历特征组合#
相对于上一种方法考虑每个预测变量的价值,这种思路是希望选出性能最好的预测变量组合。
具体搜索最优预测变量组合,有如下方式
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
All_mlr_fs = as.data.table(mlr_fselectors)
mlr_fselectors$keys()
# [1] "design_points" "exhaustive_search" "genetic_search" "random_search"
# [5] "rfe" "sequential" "shadow_variable_search"
##穷举法:比较所有可能的预测变量组合
exhaustive_search
##随机法:随机搜索若干个预测变量组合
random_search
##顺序搜索
sequential
###具体有4种思路
####向前搜索(sfs):从空模型依次添加可提高性能的特征,直到不能改进为止;
####浮动向前(sffs):从空模型,在每个步骤添加/删除对模型性能最优改进的特征,直到不再有助于改善模型性能位置
####向后搜索(sbs):从全特征模型依次删除可提高模型性能的特征,直到不能改进为止;
####浮动向后(sfbs):从全特征模型模型,在每个步骤添加/删除对模型性能最优改进的特征,直到不再有助于改善模型性能位置
##....
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
resampling = rsmp("cv")
resampling$param_set$values$folds = 3
measure = msr("regr.mse")
instance = FSelectInstanceSingleCrit$new(
task = task_regr,
learner = learner,
resampling = resampling,
measure = measure,
terminator = trm("none")
)
instance
future::plan("multisession")
fselector = fs("sequential")
fselector$param_set$values
# <ParamSet>
# id class lower upper nlevels default value
# 1: min_features ParamInt 1 Inf Inf 1 1
# 2: max_features ParamInt 1 Inf Inf <NoDefault[3]>
# 3: strategy ParamFct NA NA 2 sfs sfs
fselector$optimize(instance)
instance$result_feature_set
# [1] "Humid" "Month" "Press_height" "Temp_Monte" "Temp_Sand"
instance$result_y
# regr.mse
# 20.23275
task_regr$select(instance$result_feature_set)
learner$train(task_regr)
learner$model
# Call:
# stats::lm(formula = task$formula(), data = task$data())
# Coefficients:
# (Intercept) Humid Month Press_height Temp_Monte Temp_Sand
# 46.22527 0.10291 -0.37841 -0.01293 0.51634 0.11069
##交叉验证
resampling = rsmp("cv")
rr = resample(task_regr, learner, resampling)
rr$aggregate(msrs(c("regr.mse")))
# regr.mse
# 19.51755
|


