survival包生存分析及glmnet包lasso回归

生存分析(survival analysis)的主要目的是发现与患者生存事件相关的指标因素，例如年龄性别、基因表达/突变等。如下学习相关基础知识及几种常见的生存分析方法。

参考教程：http://www.sthda.com/english/wiki/survival-analysis-basics

1、基础知识

（1）event：表示“生存”结束的事件，最常见的形式是患者死亡，或者疾病复发等。

（2）survival time：从开始记录(通常是初次诊断患病)，到event事件发生的时间。

survival time的长短直接取决于对于事件的定义方法。
在UCSC xena整理的TCGA数据库中收集了4种事件定义方法，如下表所示。

	开始日期	结束日期(事件发生)	特征
OS (overall survial)	初次诊断	患者死亡(任何原因)	longest
DSS (disease-specific survival)	初次诊断	因该病导致死亡	/
PFI (progression-free interval)	初次诊断	经治疗后，该疾病首次恶化或导致患者死亡	shortest
DFI (disease-free interval)	初次诊断	经治疗未发现肿瘤后，又复发或导致患者死亡	/

[1] PFI里的恶化可包括疾病严重/局部区域复发/远处转移/新生肿瘤等指标。PFS(progression-free survival)指标与PFI基本类似，区别在于不关注死亡原因。

[2] DFI里的复发可包括原位复发、远处转移、新生肿瘤（同器官）。DFS(disease-free survival)指标与DFI基本类似，区别在于同样不关注死亡原因。

参考来源：

https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6066282/ Definitions and derivation of clinical survival outcome endpoints部分

OS/PFS/PFI/DFS/DFI/DSS各种生存指标定义 – 王进的个人网站 (jingege.wang)

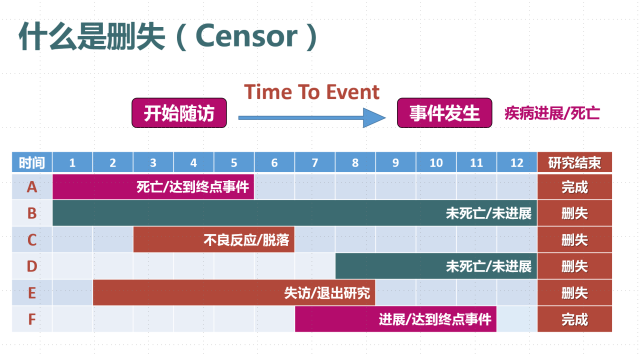
（3）Censor 删失值

在随访的过程中，可能无法全部病人都可以收集到准确地生存时间。

一方面由于随访项目时间限制，直至随访结束，病人仍在世；
一方面可能在随访期间，病人失联、或者因其它原因去世等，无法继续随访。

这样的数据就称之为Censor，而此时的生存时间即为所能记录到的最长生存时间。病人的status要么是事件发生了，要么就是Censor。

2、分析包与示例数据

（1）分析R包

1
2
3


# install.packages(c("survival", "survminer"))
library("survival") #生存分析
library("survminer") #结果可视化

（2）示例数据 lung {survival}

228个被诊断患有肺癌的病人开始长期的随访
如果病人死亡；则随访结束，并记录生存时间（从确诊到死亡的时间）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


head(lung)
#     inst time status age sex ph.ecog ph.karno pat.karno meal.cal wt.loss
# 1    3  306      2  74   1       1       90       100     1175      NA
# 2    3  455      2  68   1       0       90        90     1225      15
# 3    3 1010      1  56   1       0       90        90       NA      15
# 4    5  210      2  57   1       1       90        60     1150      11
# 5    1  883      2  60   1       0      100        90       NA       0
# 6   12 1022      1  74   1       1       50        80      513       0

# inst: Institution code
# time: Survival time in days(*) 生存时间
# status: censoring status 1=censored, 2=dead(*) 事件是否发生
# age: Age in years
# sex: Male=1 Female=2
# ph.ecog: ECOG performance score (0=good 5=dead)
# ph.karno: Karnofsky performance score (bad=0-good=100) rated by physician
# pat.karno: Karnofsky performance score as rated by patient
# meal.cal: Calories consumed at meals
# wt.loss: Weight loss in last six months

如果挖掘TCGA的数据，通常1表示事件发生，0表示censored

3、Log-rank test分析

（1）对于一种表型因素将患者分成两组，分析是否具有显著生存差异；

性别、基因突变、疾病阶段等可根据表型特性分组；
年龄、基因表达等可设置特定阈值进行分组。

（2）survfit()分析，后续可对其结果进行绘图：

n表示每组的病人数；
events表示每组有多少病人死亡；
median 表示中位生存率所对应的生存时间；
最后两列表示第三列的95%置信区间。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


fit <- survfit(Surv(time, status) ~ sex, data = lung)
print(fit)
# Call: survfit(formula = Surv(time, status) ~ sex, data = lung)
# 
# 		  n events median 0.95LCL 0.95UCL
# sex=1 138    112    270     212     310
# sex=2  90     53    426     348     550

res.sum <- surv_summary(fit)
head(res.sum[res.sum$sex==1,])
head(res.sum[res.sum$sex==2,])

（3）survdiff() 分析显著性P值

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


surv_diff <- survdiff(Surv(time, status) ~ sex, data = lung)
# Call:
#   survdiff(formula = Surv(time, status) ~ sex, data = lung)
# 
# N Observed Expected (O-E)^2/E (O-E)^2/V
# sex=1 138      112     91.6      4.55      10.3
# sex=2  90       53     73.4      5.68      10.3
# 
# Chisq= 10.3  on 1 degrees of freedom, p= 0.001

#虽然如上结果是有P值的，但是尝试之后发现从对象中只能提取chisq的值，然后再进一步转换
p.val = 1 - pchisq(surv_diff$chisq, length(surv_diff$n) - 1)
p.val
# [1] 0.001311165

（4）最优分组阈值 ☆

对于连续型变量（例如基因表达），需要手动设置一个阈值对样本进行二分组（或多分组），再进行生存分析。最常见的选择是中位数。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


### 以其中的年龄为例
median_cut = median(lung$age)
# 57
lung$age_group = ifelse(lung$age > median_cut,
                        "Old", "Young") 

table(lung$age_group)
# Old Young 
# 111   117


surv_diff <- survdiff(Surv(time, status) ~ age_group, data = lung)
p.val = 1 - pchisq(surv_diff$chisq, length(surv_diff$n) - 1)
p.val
# [1] 0.1702206

寻找最优阈值，使得组间的生存差异最显著。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


# 使用survminer包的surv_cutpoint函数
res.cut <- surv_cutpoint(lung, time = "time", event = "status",
                         variables = c("age"))
summary(res.cut)
#     cutpoint statistic
# age       70  2.013619

# best cut
best_cut = summary(res.cut)["age","cutpoint"]
# [1] 70
lung$age_group_best = ifelse(lung$age > best_cut,
                        "Old", "Young") 
table(lung$age_group_best)
# Old Young 
# 46   182

surv_diff <- survdiff(Surv(time, status) ~ age_group_best, data = lung)
p.val = 1 - pchisq(surv_diff$chisq, length(surv_diff$n) - 1)
p.val
# [1] 0.0312283
# 这里的p值结果相较上述的中位数分析更为显著

4、Log-rank test可视化

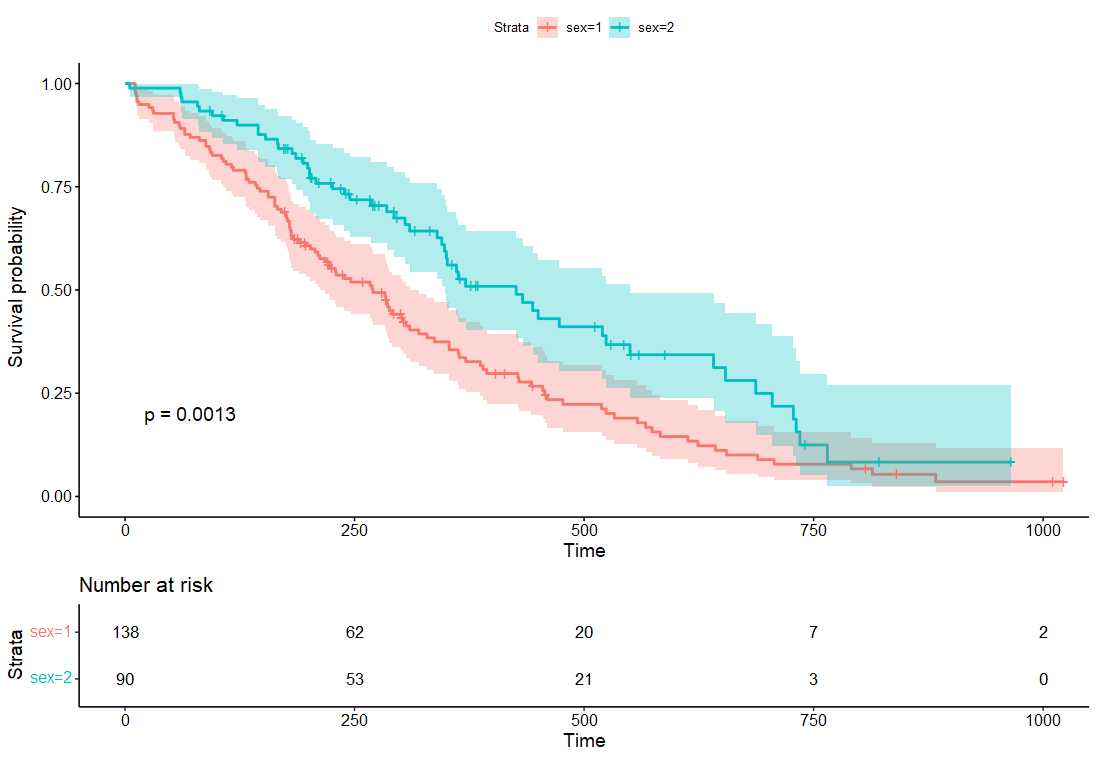
（1）绘制生存曲线，如下图所示默认绘制两个部分

上图：时间对应的生存率的生存曲线图，曲线中的短竖线表示在时间点有缺失值病人。不同颜色表示不同分组，阴影部分表示95%置信区间；左下角p值表示基于log-rank test计算得到的P值。
下表：不同时间点对应每组尚未发生事件(死亡)的数目。

1
2
3


ggsurvplot(fit,
           pval = TRUE, conf.int = TRUE,
           risk.table = TRUE)

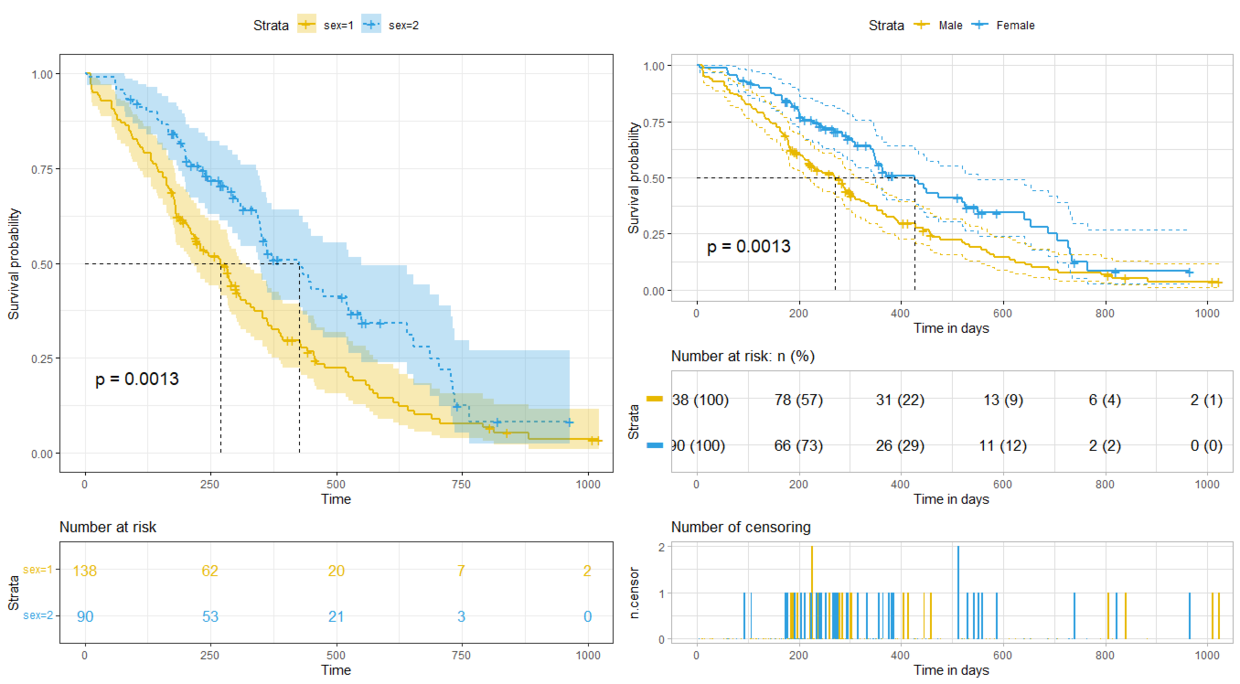
（2）可调整的图形参数(结合具体代码理解)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31


p1 = ggsurvplot(
  fit,
  pval = TRUE, conf.int = TRUE,
  risk.table = TRUE, # Add risk table
  risk.table.col = "strata", # Change risk table color by groups
  linetype = "strata", # Change line type by groups
  surv.median.line = "hv", # Specify median survival
  ggtheme = theme_bw(), # Change ggplot2 theme
  palette = c("#E7B800", "#2E9FDF")
)

p2 = ggsurvplot(
  fit,                     # survfit object with calculated statistics.
  pval = TRUE,             # show p-value of log-rank test.
  conf.int = TRUE,         # show confidence intervals for 
  # point estimaes of survival curves.
  conf.int.style = "step",  # customize style of confidence intervals
  xlab = "Time in days",   # customize X axis label.
  break.time.by = 200,     # break X axis in time intervals by 200.
  ggtheme = theme_light(), # customize plot and risk table with a theme.
  risk.table = "abs_pct",  # absolute number and percentage at risk.
  risk.table.y.text.col = T,# colour risk table text annotations.
  risk.table.y.text = FALSE,# show bars instead of names in text annotations
  # in legend of risk table.
  ncensor.plot = TRUE,      # plot the number of censored subjects at time t
  surv.median.line = "hv",  # add the median survival pointer.
  legend.labs = c("Male", "Female"),    # change legend labels.
  palette =  c("#E7B800", "#2E9FDF") # custom color palettes.
)

arrange_ggsurvplots(list(p1,p2))

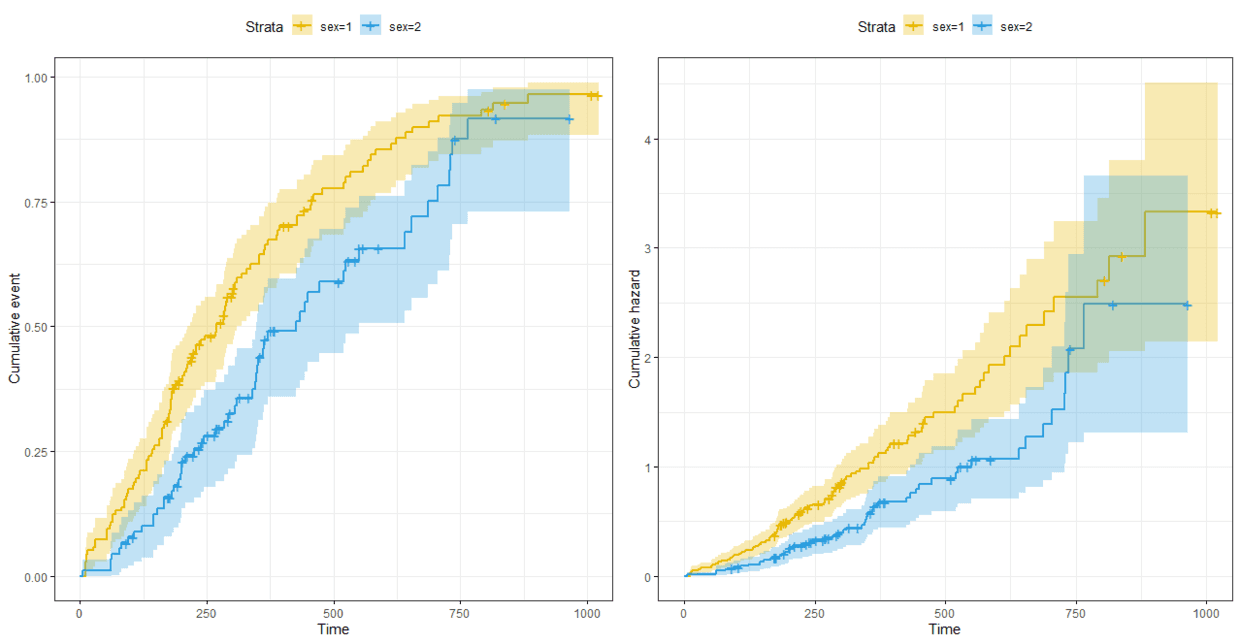
（3）如上是经典的生存曲线，同时也支持绘制其它类型曲线

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20


# 参数`fun="event"`，表示cumulative event事件累计发生率
p3=ggsurvplot(
  fit,
  conf.int = TRUE,
  risk.table.col = "strata", # Change risk table color by groups
  ggtheme = theme_bw(), # Change ggplot2 theme
  palette = c("#E7B800", "#2E9FDF"),
  fun = "event"
)
# 参数`fun="cumhaz"`，表示cummulative hazard表示累计风险水平（在时刻t，事件发生的可能性）
p4=ggsurvplot(
  fit,
  conf.int = TRUE,
  risk.table.col = "strata", # Change risk table color by groups
  ggtheme = theme_bw(), # Change ggplot2 theme
  palette = c("#E7B800", "#2E9FDF"),
  fun = "cumhaz"
)

arrange_ggsurvplots(list(p3,p4))

5、比例风险模型分析

比例风险模型又称Cox Proportional-Hazards Model，用于量化每个表型对于事件发生的影响大小。

表型可以是分类变量或者是连续变量；
衡量影响大小的指标称为Hazard rate(风险因子)，简称HR
- Hazard ratio(HR)=exp(coef)
- HR<1(coef<0) 表明负相关—该变量值越大，事件发生风险越低，生存率越高；
- HR>1(coef>0) 表明正相关—该变量值越大，事件发生风险越高，生存率越小。

（1）单变量Cox回归

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


res.cox <- coxph(Surv(time, status) ~ sex, data = lung)
res.cox
# Call:
#   coxph(formula = Surv(time, status) ~ sex, data = lung)
# 
# coef exp(coef) se(coef)      z       p
# sex -0.5310    0.5880   0.1672 -3.176 0.00149
# 
# Likelihood ratio test=10.63  on 1 df, p=0.001111
# n= 228, number of events= 165
exp(res.cox$coefficients)
# sex 
# 0.5880028

（2）对多个变量分别进行单变量Cox回归

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


#分别回归
covariates <- c("age", "sex", "ph.karno", "ph.ecog", "wt.loss")
univ_formulas <- sapply(covariates,
function(x) as.formula(paste('Surv(time, status)~', x)))
univ_models <- lapply( univ_formulas, function(x){coxph(x, data = lung)})

#提取各个变量的回归结果
univ_results <- lapply(univ_models,
                       function(x){
                         x <- summary(x)
                         p.value<-signif(x$wald["pvalue"], digits=2)
                         wald.test<-signif(x$wald["test"], digits=2)
                         beta<-signif(x$coef[1], digits=2);#coeficient beta
                         HR <-signif(x$coef[2], digits=2);#exp(beta)
                         HR.confint.lower <- signif(x$conf.int[,"lower .95"], 2)
                         HR.confint.upper <- signif(x$conf.int[,"upper .95"],2)
                         HR <- paste0(HR, " (",
                                      HR.confint.lower, "-", HR.confint.upper, ")")
                         res<-c(beta, HR, wald.test, p.value)
                         names(res)<-c("beta", "HR (95% CI for HR)", "wald.test",
                                       "p.value")
                         return(res)
                         #return(exp(cbind(coef(x),confint(x))))
                       })
res <- t(as.data.frame(univ_results, check.names = FALSE))
as.data.frame(res)
#            beta HR (95% CI for HR) wald.test p.value
# age       0.019            1 (1-1)       4.1   0.042
# sex       -0.53   0.59 (0.42-0.82)        10  0.0015
# ph.karno -0.016      0.98 (0.97-1)       7.9   0.005
# ph.ecog    0.48        1.6 (1.3-2)        18 2.7e-05
# wt.loss  0.0013         1 (0.99-1)      0.05    0.83

（3）多变量Cox回归(多元回归)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29


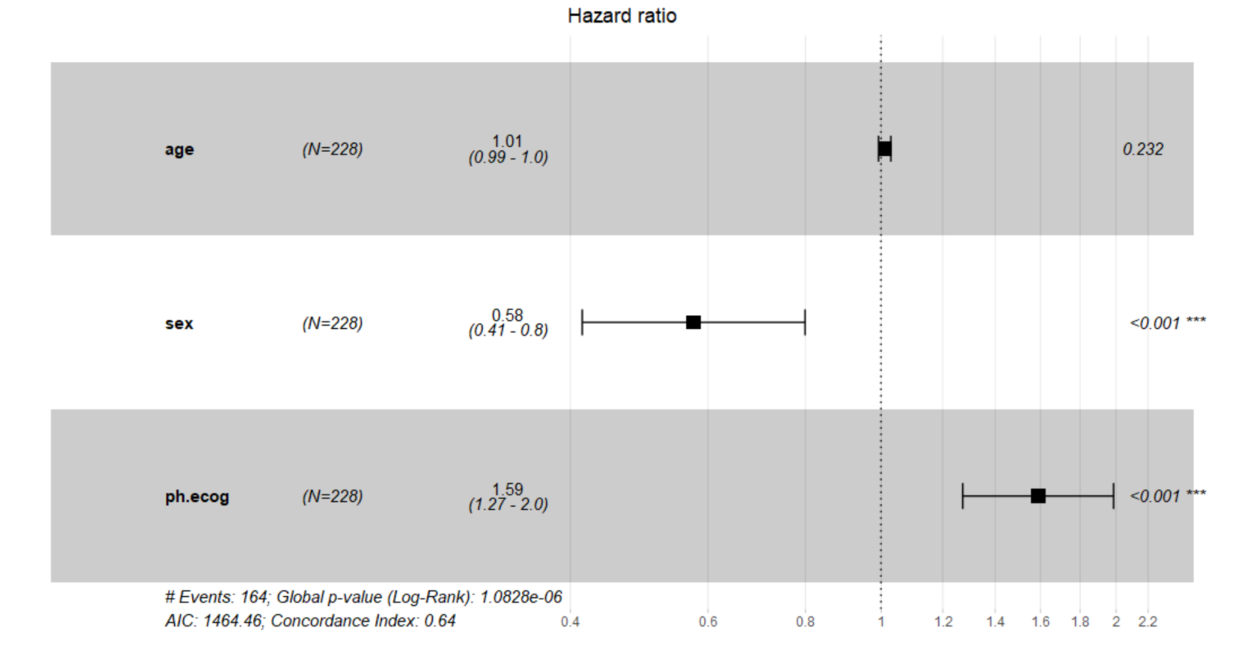
res.cox <- coxph(Surv(time, status) ~ age + sex + ph.ecog, data = lung)
summary(res.cox)
# Call:
#   coxph(formula = Surv(time, status) ~ age + sex + ph.ecog, data = lung)
# 
# n= 227, number of events= 164 
# (因为不存在，1个观察量被删除了)
# 
# 			    coef exp(coef)  se(coef)      z Pr(>|z|)    
# age      0.011067  1.011128  0.009267  1.194 0.232416    
# sex     -0.552612  0.575445  0.167739 -3.294 0.000986 ***
# ph.ecog  0.463728  1.589991  0.113577  4.083 4.45e-05 ***
#   ---
#   Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# 
# 		  exp(coef) exp(-coef) lower .95 upper .95
# age        1.0111     0.9890    0.9929    1.0297
# sex        0.5754     1.7378    0.4142    0.7994
# ph.ecog    1.5900     0.6289    1.2727    1.9864
# 
# Concordance= 0.637  (se = 0.025 )
# Likelihood ratio test= 30.5  on 3 df,   p=1e-06
# Wald test            = 29.93  on 3 df,   p=1e-06
# Score (logrank) test = 30.5  on 3 df,   p=1e-06

ggforest(res.cox, data = lung, 
         main = "Hazard ratio",
         cpositions = c(0.10, 0.22, 0.4),
         fontsize = 1.0) 

6、cox模式lasso回归

lasso回归是一种特殊的多元线性回归，可通过正则化惩罚项将冗余变量的系数变为0（即舍弃该变量）。
glmnet包可实现多种类型的lasso回归，其中包括以生存时间和事件为结局的cox回归。

1
2


install.packages("glmnet")
library(glmnet)

（1）示例数据

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


library(survival)
data(CoxExample)
x <- CoxExample$x
y <- CoxExample$y

## 标签数据(生存资料)
dim(y) 
# [1] 1000    2
head(y)
#            time status
# [1,] 1.76877757      1
# [2,] 0.54528404      1
# [3,] 0.04485918      0

## 特征数据(类似基因表达数据)
dim(x)
# [1] 1000   30
x[1:4,1:4]
#            [,1]       [,2]       [,3]       [,4]
# [1,] -0.8767670 -0.6135224 -0.5675738  0.6621599
# [2,] -0.7463894 -1.7519457  0.2854590  1.1392105
# [3,]  1.3759148 -0.2641132  0.8872741  0.3841870
# [4,]  0.2375820  0.7859162 -0.8967028 -0.8339338

（2）lasso分析

1
2
3
4
5
6


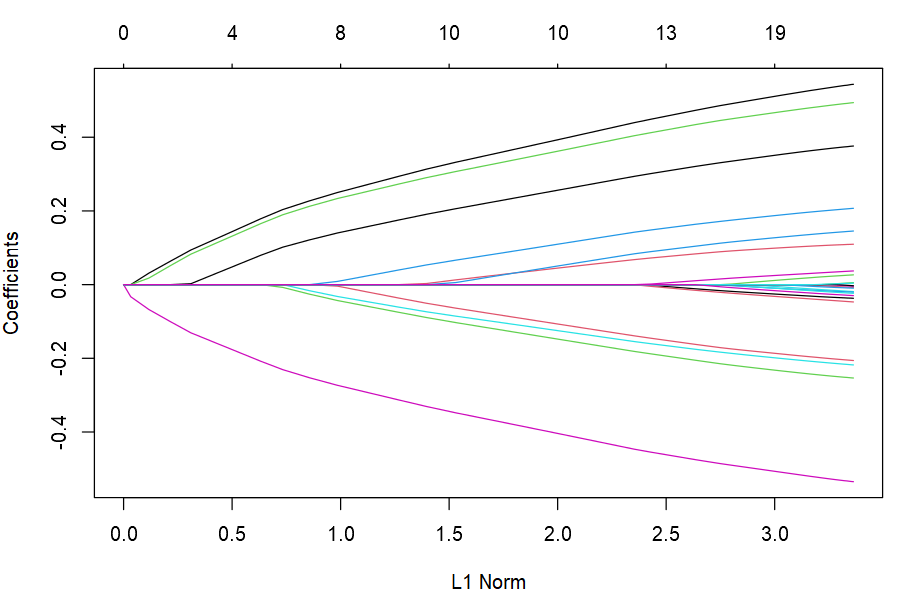
fit <- glmnet(x, y, family = "cox")
print(fit)

plot(fit, xvar = "norm", label = FALSE) # default
# plot(fit, xvar = "lambda", label = FALSE)
# plot(fit, xvar = "dev", label = FALSE)

如下图所示：

下轴：不同的L1 norm惩罚值；
上轴：在相应L1 norm惩罚值里，当前系数非0的变量个数；
左轴：变量的系数值

（3）交叉验证

在cox模式的lasso回归交叉验证中，支持两类评价指标

deviance：为默认指标；该值越小，模型预测效果越好
C：即C-index，类似AUC；该值越大，模型预测效果越好

1
2
3
4


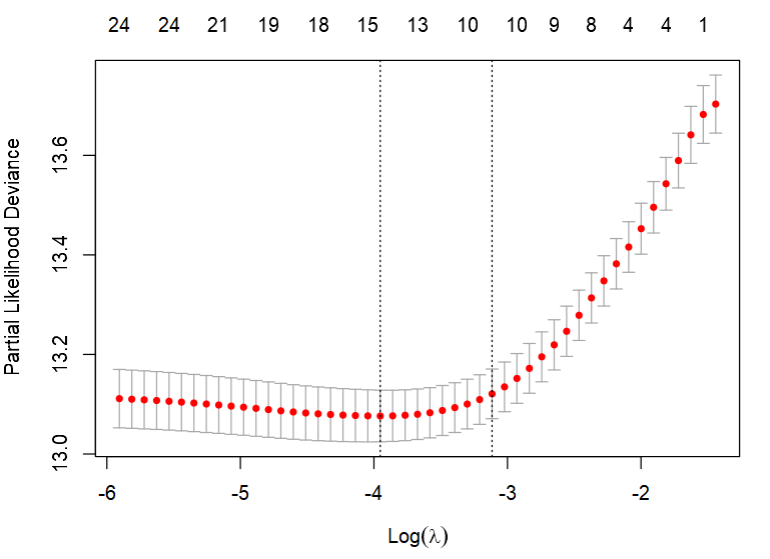
set.seed(1)
cvfit <- cv.glmnet(x, y, family = "cox", type.measure = "deviance")
# cvfit <- cv.glmnet(x, y, family = "cox", type.measure = "C")
plot(cvfit)

如下图，两条虚线分别表示两个λ值

左边的虚线→lambda.min ：表示评价指标最优的λ取值；
右边的虚线→lambda.1se：表示lambda.min的一倍标准差下对模型更为严格惩罚的λ取值。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


cvfit$lambda.min
# [1] 0.01920429
cvfit$lambda.1se
# 1] 0.04436439

coef(cvfit, s = cvfit$lambda.min)

library(tidyverse)
coef(cvfit, s="lambda.min") %>% 
  as.matrix() %>% as.data.frame() %>% 
  tibble::rownames_to_column(var = "mRNA") %>% 
  dplyr::rename(coef=`1`) %>% 
  dplyr::filter(coef!=0)
#    mRNA        coef
# 1    V1  0.47972069
# 2    V2 -0.16674492
# 3    V3 -0.21014303
# 4    V4  0.16781912
# 5    V5 -0.17951289
# 6    V6 -0.48058218
# 7    V7  0.32603876
# 8    V8  0.08646499
# 9    V9  0.44014703
# 10  V10  0.10854409
# 11  V13  0.01304299
# 12  V17 -0.01388096
# 13  V25 -0.01830447
# 14  V30 -0.00301953

1、基础知识#

2、分析包与示例数据#

3、Log-rank test分析#

4、Log-rank test可视化#

5、比例风险模型分析#

6、cox模式lasso回归#