1、决策树基础#
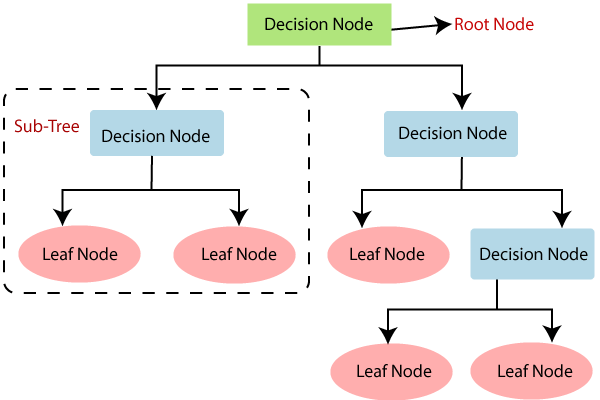
1.1 决策树的构成#
(1)决策树由节点组成,可分为决策节点(Decision tree)与叶节点(leaf node)。
(2)从上到下的第一个节点也称为根节点(Root Node)。根节点到叶节点的最长距离称为树的深度。
(3)对于每一个决策节点,选择样本集的一个最佳预测变量,确定最佳的阈值,进行二分类;最后根据叶节点类别的众数进行分类(均数进行回归)。
1.2 基尼系数#
(1)决策树为了使表示数据杂乱程度的不纯度减小,选择预测变量的最佳cut-off进行分割。当分割出来的每个组中的标签大部分属于同种标签时,不纯度会变小。
- 每一组的复杂度可通过基尼指数表示。其值越小,表示数据纯度越高
- 分割前后的数据复杂度变化可通过基尼增益表示。其值越大,表示数据的纯度变得越高。
(2)基尼指数与基尼增益的计算方法如下图所示:
如公式所示,对于二分类任务的基尼指数取值范围应为0~0.5之间。当等于0时,表示由同一种标签样本组成;当等于1时,表示两个标签样本各占一半。

(3)比较不同预测变量的基尼增益,其实就是比较把不同预测变量的最佳分割cut-off下的基尼增益。
具体对于不同类型的预测变量,如上图所示,有不同的选择方法(从若干候选值中选择一个最佳的,作为该预测变量的代表)
1.3 防止决策树过拟合#
(1)直接限制最长深度;
(2)每一次划分所引起的最小性能改进(cp值,类似于基尼增益);
(3)叶节点size:如果划分一个节点会导致叶节点中包含的样本数少于规定值,则不会划分;
(4)决策节点size:如果决策节点少于规定值,则不会被划分。(就被视为了叶节点)
2、mlr建模#
2.1 动物特征数据集#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
data(Zoo, package = "mlbench")
zooTib <- Zoo
#将逻辑变量(True/False)转为数值型因子变量
zooTib <- mutate_if(zooTib, is.logical, as.factor)
str(zooTib)
# 'data.frame': 101 obs. of 17 variables:
# $ hair : Factor w/ 2 levels "FALSE","TRUE": 2 2 1 2 2 2 2 1 1 2 ...
# $ feathers: Factor w/ 2 levels "FALSE","TRUE": 1 1 1 1 1 1 1 1 1 1 ...
# $ eggs : Factor w/ 2 levels "FALSE","TRUE": 1 1 2 1 1 1 1 2 2 1 ...
# $ milk : Factor w/ 2 levels "FALSE","TRUE": 2 2 1 2 2 2 2 1 1 2 ...
# $ airborne: Factor w/ 2 levels "FALSE","TRUE": 1 1 1 1 1 1 1 1 1 1 ...
# $ aquatic : Factor w/ 2 levels "FALSE","TRUE": 1 1 2 1 1 1 1 2 2 1 ...
# $ predator: Factor w/ 2 levels "FALSE","TRUE": 2 1 2 2 2 1 1 1 2 1 ...
# $ toothed : Factor w/ 2 levels "FALSE","TRUE": 2 2 2 2 2 2 2 2 2 2 ...
# $ backbone: Factor w/ 2 levels "FALSE","TRUE": 2 2 2 2 2 2 2 2 2 2 ...
# $ breathes: Factor w/ 2 levels "FALSE","TRUE": 2 2 1 2 2 2 2 1 1 2 ...
# $ venomous: Factor w/ 2 levels "FALSE","TRUE": 1 1 1 1 1 1 1 1 1 1 ...
# $ fins : Factor w/ 2 levels "FALSE","TRUE": 1 1 2 1 1 1 1 2 2 1 ...
# $ legs : int 4 4 0 4 4 4 4 0 0 4 ...
# $ tail : Factor w/ 2 levels "FALSE","TRUE": 1 2 2 1 2 2 2 2 2 1 ...
# $ domestic: Factor w/ 2 levels "FALSE","TRUE": 1 1 1 1 1 1 2 2 1 2 ...
# $ catsize : Factor w/ 2 levels "FALSE","TRUE": 2 2 1 2 2 2 2 1 1 1 ...
# $ type : Factor w/ 7 levels "mammal","bird",..: 1 1 4 1 1 1 1 4 4 1 ...
##第1~16列为动物特征
##第17列为动物名标签
|
2.2 确定预测目标与训练方法#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
#(1)根据1-16列动物特征进行动物类型预测
zooTask <- makeClassifTask(data = zooTib, target = "type")
#使用决策树rpart分类算法
tree <- makeLearner("classif.rpart")
##(2)确定该算法的超参数空间以及遍历方法
getParamSet(tree)
treeParamSpace <- makeParamSet(
makeIntegerParam("minsplit", lower = 5, upper = 20),
makeIntegerParam("minbucket", lower = 3, upper = 10),
makeDiscreteParam("cp", values = seq(0.01,0.1,0.01)),
makeIntegerParam("maxdepth", lower = 3, upper = 10))
# 16*8*10*8=100240
randSearch <- makeTuneControlRandom(maxit = 200)
##(3)交叉验证方法
cvForTuning <- makeResampleDesc("CV", iters = 5)
|
2.3 模型训练#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
##(1)确定最佳超参数组合
library(parallel)
library(parallelMap)
#调用多线程
parallelStartSocket(cpus = detectCores())
tunedTreePars <- tuneParams(tree, task = zooTask, # ~30 sec
resampling = cvForTuning,
par.set = treeParamSpace,
control = randSearch)
#停用多线程
parallelStop()
tunedTreePars
# Tune result:
# Op. pars: minsplit=6; minbucket=3; cp=0.0345; maxdepth=9
# mmce.test.mean=0.1200000
##(2)使用上述组合训练模型
tunedTree <- setHyperPars(tree, par.vals = tunedTreePars$x)
tunedTreeModel <- train(tunedTree, zooTask)
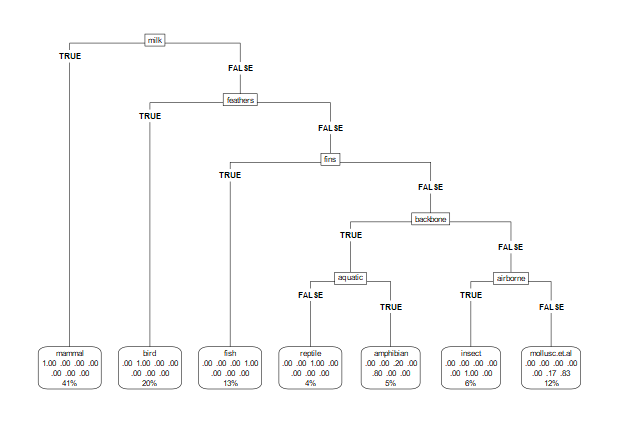
##(3)可视化决策树
treeModelData <- getLearnerModel(tunedTreeModel)
library(rpart.plot)
rpart.plot(treeModelData, roundint = FALSE, type = 5)
|
2.4 嵌套交叉验证#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
#inner
inner <- makeResampleDesc("CV", iters = 5)
#outer
outer <- makeResampleDesc("CV", iters = 3)
treeWrapper <- makeTuneWrapper("classif.rpart", resampling = inner,
par.set = treeParamSpace,
control = randSearch)
parallelStartSocket(cpus = 8)
cvWithTuning <- resample(treeWrapper, zooTask, resampling = outer)
parallelStop()
cvWithTuning
# Resample Result
# Task: zooTib
# Learner: classif.rpart.tuned
# Aggr perf: mmce.test.mean=0.1295306
# Runtime: 13.4196
|


