重抽样本质上是从观测数据中反复抽取数据，有两种不同用法

1、Bootstrap

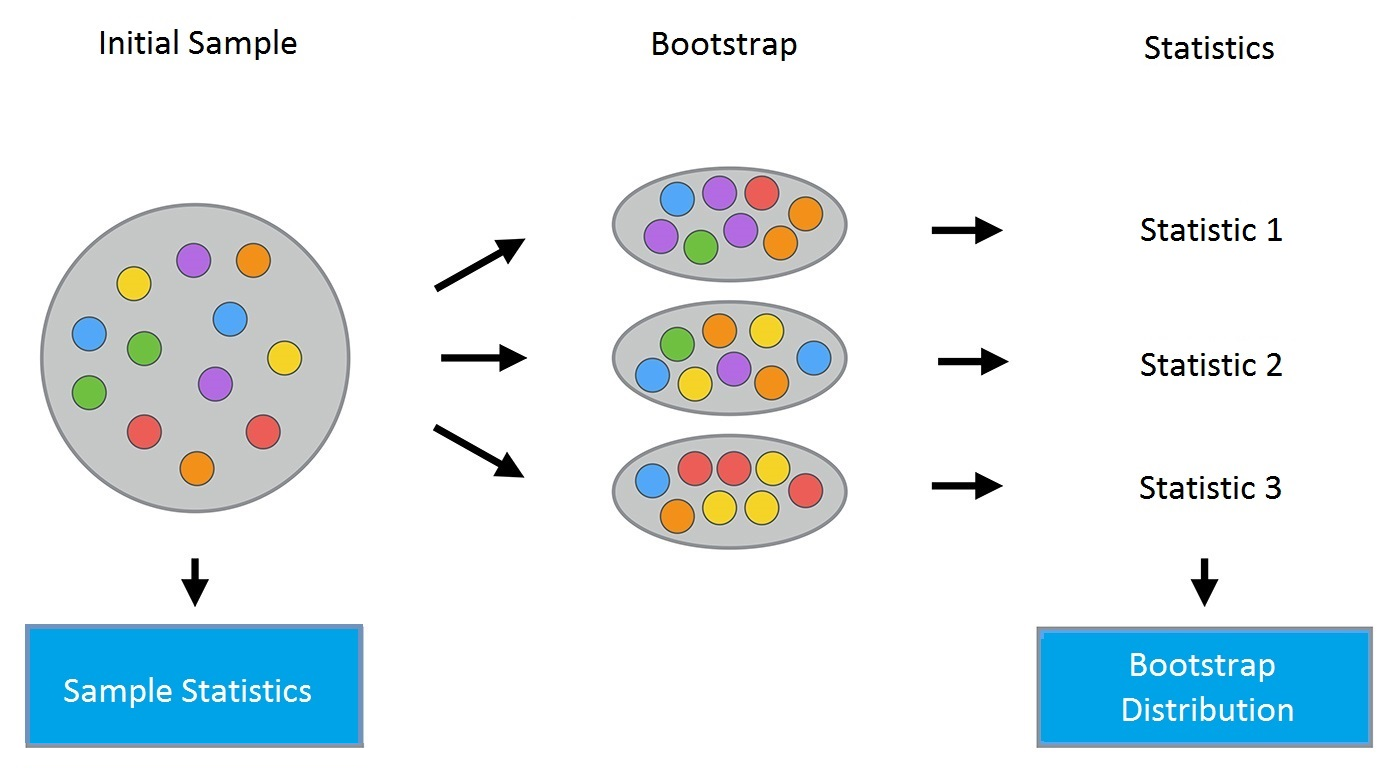
（1）Bootstrap的核心是有放回的抽样，常用于估计统计量(例如均值等)置信区间

• 在样本数据符合正态分布的情况，可基于中心极限定理使用标准误计算公式计算置信区间。详见之前的笔记002

• 在样本数据不符合正态分布或者分布未知的情况下，则可以使用如下的Bootstrap法

（2）如上所述，Bootstrap使用有放回的抽样方式，抽取等容量的随机样本，重复多次。根据每次得到的新样本，计算相应的统计量。

计算置信区间的方式：对n次抽样的统计量(均数)结果，分别计算出2.5%分位数与97.5%分位数，这两个值的区间就是样本统计量(均数)的95%置信区间。

2、置换检验

置换检验permutation test是计算假设检验的显著性(P值)的方式之一。

如果样本数据符合正态分布，可使用基于极限中心定理的公式计算。如果不符合正态分布，之前提到可以使用秩和检验方法

例如

首先计算患者组的均值为13.2，健康组的均值为10，两组均值差为3.2

接下来使用置换检验方式，评价出差值3.2是否具有显著性。

（1）将8个数据打乱、合并为一个数据集

（2）从中随机抽取(不放回)5个样本作为“患者组”、剩余的3个样本作为“健康组”，计算这新的两组均值差，记录下来

（3）多次重复步骤（2），产生大量由置换迭代得到的均值差，得到Permutation Test Distribution。

（4）观察真实均值差3.2在上述Distribution的位置，计算P值。如果真实均值差位于分布尾端，说明这种差异不是由随机性造成的，即具有显著性。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

dat = data.frame(score = c(12, 15, 11, 14, 14, 10, 11, 9),
                 group = factor(c(rep("A",5), rep("B",3)))) 
dat
#   score group
# 1    12     A
# 2    15     A
# 3    11     A
# 4    14     A
# 5    14     A
# 6    10     B
# 7    11     B
# 8     9     B


library(coin)
oneway_test(score ~ group, data=dat, distribution="exact") 
# 	Exact Two-Sample Fisher-Pitman Permutation Test

# data:  score by group (A, B)
# Z = 2.0494, p-value = 0.05357
# alternative hypothesis: true mu is not equal to 0

• 更多置换检验应用方差分析、回归分析等详见https://www.jianshu.com/p/86ec855805d6