1、混淆矩阵相关指标
假设某医生对100个挂号的人进行某疾病的判断,具体情况如下
- 前提已知这100人的真实患病情况:60人患病,40人健康
- 医生根据症状判断(预测)结果为:80人患病,20人健康
| 真实-患病 | 真实-健康 | |
|---|---|---|
| 预测-患病 | 50 | 30 |
| 预测-健康 | 10 | 10 |
根据医生的预测结果,将预测为患病定义为阳性(Positive)事件;预测为健康状态为阴性(Negative)事件
如果医生的预测与挂号人的真实情况一致,则认为是True;否则认为是False。
于是上面四个数字分别对应四种情况–
| 混淆矩阵 | 真实-患病 | 真实-健康 |
|---|---|---|
| 预测-患病 | True Positive(TP) | False Positive(FP) |
| 预测-健康 | False Negative(FN) | True Negative(TN) |
(1)正确率:预测正确的结果占总预测结果的比例。Accuracy
- (50+10)/(50+10+30+10)=0.6
$$ Accuracy = \frac{TP + TN}{TP + TN + FP + FN} $$
(2)精确率:在所有预测为阳性的结果里,预测正确的比例。Precision
- 50/(50+30) = 0.625
$$ Precision = \frac{TP}{TP + FP} $$
(3)召回率:在实际为阳性的数据中,预测正确的比例。也称为敏感度。Sensitivity/Recall
- 50/(50+10) = 0.833
$$ Sensitivity /Recall = \frac{TP}{TP + FN} $$
(4)特异度:在实际为阴性的数据中,预测正确的比例。Specifity
- 10/(10+30) = 0.25
$$ Specifity = \frac{TN}{TN+FP} $$
如果医生将判断疾病的标准提高,那么对于医生预测患病的精确率将提高;但是症状不明显的患病人将会判断为健康,即召回率降低。反之如果将判断疾病的标准降低,则精确率降低、召回率增高。
(5)F1值:综合反映了精确率和召回率两个指标的情况
- 2×(0.625×0.833)/(0.625+0.833) = 0.714
$$ F1 = 2\cdot \frac{Precision \cdot Recall}{Precision + Recall} $$
2、ROC曲线与PR曲线
(1)ROC曲线
在机器学习二分类预测模型的结果通常为0~1之间的概率值。越接近1,表明是阳性的可能性越高。
通过设定一个阈值(如0.5)作为最终的二分类判断结果,进而计算得到对应的混淆矩阵。
对于不同阈值(0~1之间)得到的混淆矩阵都可以计算两个指标
- (1)真阳性率True Positive Rate:对于实际患病的人,诊断为患病的概率。对应上面的召回率/敏感度;
- (2)假阳性率False Positive Rate:对于实际健康的人,诊断为患病的概率。对应上面的(1-特异度)。
对于所有可能阈值,都可以得到一组(假阳性率,真阳性率)数据,可如下绘制出ROC曲线。
- 如果诊断标准(阈值)的提高,那么假阳性率与真阳性率都会降低。极端情况,将所有人都判断为健康。
- 如果诊断标准(阈值)的降低,那么假阳性率与真阳性率都会提高。极端情况,将所有人都判断为患病。
ROC曲线的线下面积总和称为AUC,也称AUROC。一般AUC的取值范围在0.5和1之间。越接近1,表示模型的分类效果越好。

(2)PR曲线
PR曲线反映了召回率与精确率之间的关系。PR曲线下面积称为AUPR。
- 召回率:在实际为阳性的数据中,预测正确的比例。也称为敏感度。即ROC曲线的真阳性指标。
- 精确率:在所有预测为阳性的结果里,预测正确的比例。

AUROC与AUPR都可以用于机器学习二分类预测模型的评价指标,均适用于正负样本不平衡的数据集。
当样本数据集中的阴性样本远多于阳性样本时:
-
如果关注模型对正负样本正确分类的整体情况,则AUROC更合适。
-
如果关注模型对正样本的正确分类情况,则AUPR更合适。
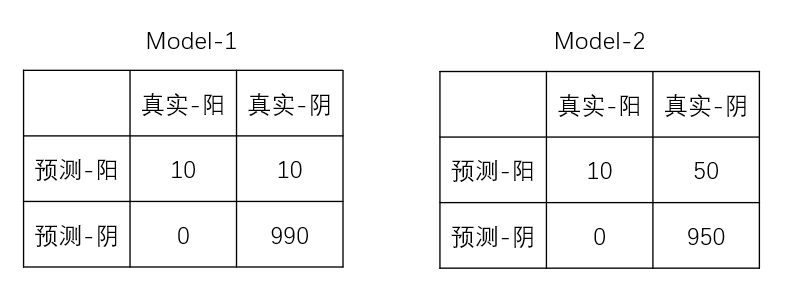
AUROC与AUPR的主要区别在于前者使用了假阳性指标(FPR),后者是使用了精确率指标(Precision)
-
对于Model-1:FPR=10/(10+990)=0.01;Presion=10/(10+10)=0.5;TPR=1
-
对于Model-2:FPR=50/(50+950)=0.05;Precison=10/(10+50)=0.16;TPR=1
相比于模型1,模型2会将更多的阴性样本预测为阳性。
但由于阴性样本非常多,导致兼顾正负类预测情况的AUROC变化不明显;
而AUPR专注与正类样本的分类情况,此时AUPR值会下降较为明显。