一、相关性

1、线性相关系数

（1）线性相关系数用于描述多个样本数据中两个变量之间的线性相关的程度。

  • 变量通常为连续型变量；
  • 两个变量一般为描述样本的不同指标，例如人群的体重值与血糖值

（2）协方差(Corvariance)：用于衡量两个随机变量的联合变化程度。

  • 如果协方差大于0，表示正相关；小于0表示负相关。

$$ Cov(y, x) = \frac{\sum_{i=1}^n(y_i-\overline{y})(x_i-\overline{x})}{n-1} $$

如上公式，可以看出方差其实是协方差的特例。自己对自己的关系就是方差。

（3）为了克服不同变量的尺度不相同所带来的的干扰，在计算需要对原始变量进行标准正态分布转换。此时得到的协方差就是两个连续变量的线性相关系数，常称为Person相关系数。 $$ r = \frac{\sum_{i=1}^n(y_i-\overline{y})(x_i-\overline{x})}{\sqrt{\sum_{i=1}^n(y_i-\overline{y})^2}\sqrt{\sum_{i=1}^n(x_i-\overline{x})^2}} $$

  • r(r>0)值越大表示两个变量呈正相关；r(r<0)值越小表示两个变量呈负相关；r=0表示两个变量不相关。

（4）P值与假设检验

  • 在相关性分析的假设检验中，零假设通常为r=0。在p值显著的情况下，可认为两个变量存在相关性，仅此而已。
  • 不能说P值越小，两个变量的相关性越强(包括正负)。
  • 当P值不显著时，所能得到的结论是两个变量不存在线性相关；而不是不相关。

2、基于秩次的相关系数

当连续变量值的分布特征不符合正态分布时，一般不可使用Person相关系数，可选择如下基于秩次的计算方式。

2.1 Spearman相关系数

计算思路比较简单：首先求出每个变量各自排序后的秩次，然后以秩次作为变量计算其Person相关系数。

Spearman&rsquo;s rank correlation coefficient - Wikipedia

在计算秩次时，如果对于某一变量，多个样本的值相同的情况，则称为Tie或者说是打结。此时一般取秩次的平均值。如下例图所示。

Sample Var1 Var1-Rank
Sp1 1.1 1
Sp2 2.5 2.5
Sp3 2.5 2.5
Sp4 4.9 4

2.2 Kendall的tau系数

（1）首先对于每个变量(Var1, Var2)，计算每个样本的样本秩次。

（2）然后随机抽取一对样本Sp1，Sp2：

  • 如果Sp1的Var1秩次大于(小于)Sp2的Var1秩次，同时Sp1的Var2秩次也大于(小于)Sp2的Var2秩次，则记为Concordant，简记为C；
  • 如不符合上述情况，则记为Discordant，简记为D。
Kendall's tau calculation

（3）最后统计对于所有两两组合的情况下，C与D的差值所占的比例，即为tau系数。

  • tau值越高表明两个变量越相关。

$$ \tau = \frac{C-D}{n(n-1)/2} $$

在涉及有序分类(等级)变量的相关性时，可以转换为基于秩次的相关性计算。

此时会存在很多打结的秩次数据，此时使用Tau/b系数相对Spearman可以更好地处理打结数据。

3、R实操

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

a1 = c(1,2,4,5,8,11)
a2 = c(2,3,5,7,6,15)
cor(a1, a2)
# [1] 0.9136724
cor(a1, a2, method = "pearson")  # default
cor(a1, a2, method = "kendall")  
cor(a1, a2, method = "spearman")  


cor.test(a1, a2)
# data:  a1 and a2
# t = 4.4959, df = 4, p-value = 0.01086
# alternative hypothesis: true correlation is not equal to 0
# 95 percent confidence interval:
#  0.3950157 0.9906589
# sample estimates:
#       cor 
# 0.9136724 
cor.test(a1, a2)$p.value
cor.test(a1, a2, method = "pearson")  # default
cor.test(a1, a2, method = "kendall")  
cor.test(a1, a2, method = "spearman")

二、一致性

一致性与相关性的区别体现在如下两个方面

  • 一致性强调是描述同一指标的不同测量方式的关系。例如仪器A测量体重值与仪器B测量体重值的一致性。

  • 一致性更注重两个指标的尺度上的一致性，即[1,2,3]与[1.1,1.9,2.8]的一致性更高；而与[2,4,6]的一致性则较低。

2.1 CCC

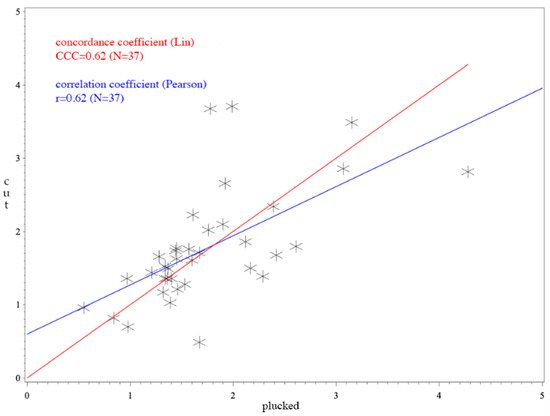
CCC(Concordance Correlation Coefficient)用偏离45度线的程度，对Pearson相关系数进行校正。

  • 计算公式如下：其中r–相关系数；Sx–变量x的标准差；x(hat)–变量x的均值

$$ r_c = \frac{2r\cdot S_xS_y}{S_x^2+S_y^2+(\overline{x}-\overline{y})^2} $$

  • 如下图所示，展现了CCC与线性相关系数的不同之处。

Animals | Free Full-Text | Validation of an Alternative Feather Sampling Method to Measure Corticosterone | HTML

2.2 Kappa系数

Cohen’s Kappa

（1）Kappa系数用于分类变量的一致性评价。值范围在 -1 ~ 1之间，越接近1表示一致性越好。

  • 可用于机器学习中评价模型分类预测能力。
  • 例如真实的有效、无效所预测的有效、无效的一致性程度。

计算公式如下：其中Po表示观察的一致性，即同一样本的两个变量分类结果相同；Pe表示期望的一致性，即同一样本一致性的期望频率 $$ \kappa = \frac{p_o - p_e}{1 - p_e} $$

（2）举例来说，需要对一批产品(N=20)进行质量评价，分为A、B、C 这3个等级。两个质检员分别独自评价分类，使用kappa系数计算两次结果的一致性。

A B C sum
A 8 2 1 11
B 2 3 0 5
C 0 1 3 4
sum 10 6 4 20

$$ p_o = \frac{8}{20} + \frac{3}{20}+ \frac{3}{20} = 0.70 $$

$$ p_e = \frac{10}{20}\cdot\frac{11}{20}+\frac{6}{20}\cdot\frac{5}{20}+\frac{4}{20}\cdot\frac{4}{20} = 0.39 $$

$$ \kappa = \frac{0.7 - 0.39}{1-0.39} = 0.51 $$

（3）加权kappa系数：适用于有序分类变量的一致性评价。

  • 还是上面的例子，如果A、B、C分别表示好、中、差3个有序等级。

  • 把同一个产品标记为A、B的情况与把同一个产品标记为A、C的一致性差异是不一致的，前者会比后者更好一些。

如下为一个示例的权重矩阵

A B C
A 1 0.5 0
B 0.5 1 0.5
C 0 0.5 1

把同一产品分为同一等级的一致性最高，故赋予最高的权重

把同一产品分为相差一级的一致性中等，故赋予较低的权重

把同一产品分为相差两级的一致性最低，故赋予最低的权重

所以加权的观察一致性计算如下

A B C sum
A 8×1=8 2×0.5=1 1×0=0 9
B 2×0.5=1 3×1=3 0×0.5=0 4
C 0×0=0 1×0.5=0.5 3×1=3 3.5
sum 9 4.5 3 16.5

$$ p_o = \frac{16.5}{20} = 0.825 $$

加权的预期一致性计算如下

A B C sum
A 10×11×1=110 6×11×0.5=33 4×11×0=0 143
B 10×5×0.5=25 6×5×1=30 4×5×0.5=10 65
C 10×4×0=0 6×4×0.5=12 4×4×1=16 28
sum 135 75 26 236

$$ p_e = \frac{236 }{20×20} = 0.59 $$

$$ \kappa = \frac{0.825 - 0.59}{1-0.59} = 0.57 $$

未加权矩阵相当于多角线元素值为1，其余元素值为0的权重值矩阵。

2.3 AC系数

Gwet’s AC1 $$ AC1 = \frac{p-e(\gamma)}{1-e(\gamma)} $$

P：the overall percent agreement $$ P = \frac{A+D}{N} $$ e(γ): the chance agreement probability

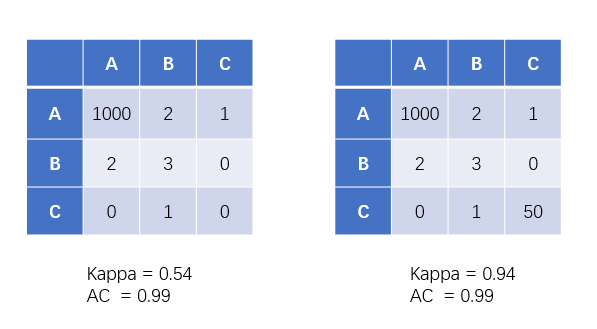
相比Kappa系数，AC系数对边际分类问题准确性有更高的容忍度。

image-20220619125237859

2.4 R实操

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

##(1) CCC系数
a1 = c(1,2,4,5,8,11)
a2 = c(2,3,5,7,6,15)

library(DescTools)
CCC(a1, a2)
# $rho.c
# est    lwr.ci   upr.ci
# 1 0.8550984 0.3990051 0.971993
# 
# $s.shift
# [1] 1.230973
# 
# $l.shift
# [1] 0.3060408
# 
# $C.b
# [1] 0.9358917
# 
# $blalt
# mean delta
# 1  1.5    -1
# 2  2.5    -1
# 3  4.5    -1
# 4  6.0    -2
# 5  7.0     2
# 6 13.0    -4


##(2) Kappa系数
library(vcd)
library(vcd)
mat = matrix(c(10, 2, 1,
               2, 3 ,0,
               0, 1 ,3), 
             byrow = T, nrow = 3)
colnames(mat) = c("A","B","C")
rownames(mat) = c("A","B","C")
mat
#    A B C
# A 10 2 1
# B  2 3 0
# C  0 1 3
Kappa(mat)
#             value    ASE     z  Pr(>|z|)
# Unweighted 0.5319 0.1611 3.301 0.0009629
# Weighted   0.5969 0.1554 3.841 0.0001224
Kappa(mat)$Weights
#      [,1] [,2] [,3]
# [1,]  1.0  0.5  0.0
# [2,]  0.5  1.0  0.5
# [3,]  0.0  0.5  1.0

##(3)

$$ AC1 = \frac{p-e(\gamma)}{1-e(\gamma)} $$

$$ p = \frac{a_1 + a_5 + a_9}{\sum_{i=1}^{9}a_i} $$

$$ e(\gamma) = 2q(1-q), \quad q=\frac{(a_1 + a_2 + a_3)+(a_1+a_4+a_9)}{2\sum_{i=1}^{9}a_i} $$