方差分析(analysis of variance)可以简单的理解为多组间的均值比较。例如A班、B班、C班、D班的考试成绩均值是否存在显著差异。方差分析是基于F分布的假设检验，所以又称F检验

What is Analysis of Variance (ANOVA)? | TIBCO Software

方差分析

1、分析步骤

1.1 明确问题，做出假设

零假设为组间（假设有k组）均值相同。备择假设表示为k组中至少有两组不相等。

k表示组别数，nj表示第j组的样本数，xij表示第j组的第i个样本；(hat)x表示总均值。根据分组信息，可以将总变异分解为组间方差与组内误差两部分

$$ H_0 : \mu_1=\mu_2= … =\mu_k $$

1.2 方差分解

（1）所有样本的总方差计算即所有组样本与总均值的差值的平方和。然后可将总分差分解为组间方差与组内方差两部分。

  • 总方差计算公式

$$ SS_{total} = \sum_{j=1}^{k} \sum_{i=1}^{n_j}(x_{ij}-\overline{x})^2 $$

（2）组间误差：分析组与组之间的差异。如果分组变量对结果有很大的影响，那么组间差异应该很大。

  • 组间方差计算公式

$$ SS_{between} = \sum_{j=1}^{k}n_{j}(\overline{x}_{j} - \overline{x})^2 $$

（3）组内方差：组内样本由于个体随机性造成差异。这种差异占比理论上应该越小越好，则每组的水平都很一致。

  • 组内方差计算公式

$$ SS_{within} = \sum_{j=1}^{k} \sum_{i=1}^{n_j}(x_{ij}-\overline{x}_j)^2 $$

1.3 计算F统计量

（1）在零假设的前提下，组间方差等于0。而如果预期分类变量对样本结果影响很大，那么组间方差应远大于组内方差。

$$ SS_{total} = SS_{between} + SS_{within} $$

（2）因此可计算F统计量表示组间方差与组内方差的比值，其中分子的自由度为（k-1），分母的自由度为（N-k）。 $$ F = \frac{\frac{SS_{between}}{k-1}}{\frac{SS_{within}}{N-k}} $$

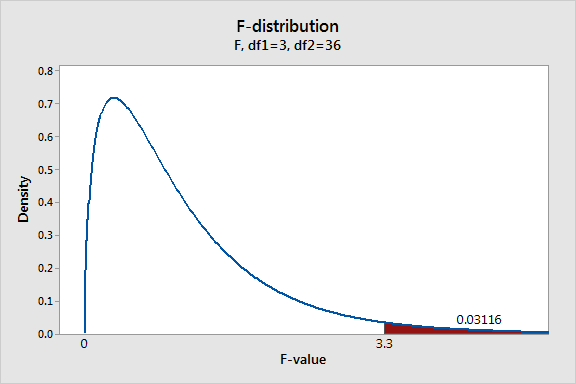
（3）在零假设成立的情况下，F统计量符合自由度组合为[(k-1), (N-k)]的F分布。据此计算出当前F统计量对应的P值结果。

How F-tests work in Analysis of Variance (ANOVA) - Statistics By Jim

2、注意事项

2.1 变异分解与分组变量

如上方差分析的本质是变异(方差)分解。在给定一样本数据的总变异的前提下，观测指定的分组(分类)变量对于总变异的贡献度或者说解释度。在此基础上有一些衍生。

  • 多因素方差分析

    可能存在多个分组(健康/不健康、男女)变量共同影响样本的总变异，且这些影响具有可加性，即独立的。(不独立的情况即存在交互效应)

  • 回归分析

    换一个角度思考回归分析也属于方差分解。即分组变量为连续变量，以分析该自变量对样本数据的影响是否占总变异的主要部分。

2.2 Kruskal-Wails秩和检验

方差分析的重要前提是组间方差齐性与正态性。即每组数据的方差相等，且均符合正态分布。如不符合正态分布的假设，可以使用Kruskal-Wails秩和检验的非参数检验方法。

符合正态分布 不符合正态分布
两组间均值比较 T检验 Wilcoxon秩和检验
多组间均值比较 方差分析 Kruskal-Wails秩和检验

2.3 两两比较与P值校正

根据方差分析的零假设，在P值显著的情况下所能得到结论是至少存在两组间均值不同。如果想知道哪两组存在不同则需要进行两两比较（T检验）。

如果连续进行多次T检验，则一类错误概率会增加。例如将P值定义0.05，那么连续比较20次，则至少会有一次假阳性的结果发生；或者理解为 (1-0.05)^20=0.36，即只有36%的把握，认为20次比较中没有假阳性发生。

因此需要对原始P值进行调整，获得adjusted P-value，有如下方法

  • FDR/BH(Benjamini & Hochberg)：多重比较在所有拒绝H0的次数中，错误拒绝H0(假阳性)所占的比例

  • Bonferroni：根据比较的次数，将一类错误率控制在0.05/k之内。在比较次数比较多时，较为严苛

    • Holm，也称step-down Bonferroni法，不会太严苛
    • Hochberg，也称step-up Bonferryoni法，不会太严苛

本质是对给定的一串P值进行调整；调整之后的值普遍比原始值高一点，所以在下结论时假阳性率会低一点。

R Companion: Multiple Comparisons

3、R实操

  • 示例数据
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

#加载示例数据集：五种降低胆固醇疗法的结果
library(multcomp)
data(cholesterol)
head(cholesterol)
#     trt response
# 1 1time   3.8612
# 2 1time  10.3868
# 3 1time   5.9059
# 4 1time   3.0609
# 5 1time   7.7204
# 6 1time   2.7139
table(cholesterol$trt)
# 1time 2times 4times  drugD  drugE 
#    10     10     10     10     10
  • 方差分析
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

fit = aov(response ~ trt, data = cholesterol)
summary(fit)
# Df Sum Sq Mean Sq F value   Pr(>F)    
# trt          4 1351.4   337.8   32.43 9.82e-13 ***
# Residuals   45  468.8    10.4                     
# ---
# Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

summary(fit)[[1]][1,5]  # Pr(>F) 
# [1] 9.818516e-13

此外aov()还支持单因素协方差分析，双因素方差分析等

  • Tukey多重两两比较
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

TukeyHSD(fit)
# Tukey multiple comparisons of means
# 95% family-wise confidence level
# 
# Fit: aov(formula = response ~ trt, data = cholesterol)
# 
# $trt
#                   diff        lwr       upr     p adj
# 2times-1time   3.44300 -0.6582817  7.544282 0.1380949
# 4times-1time   6.59281  2.4915283 10.694092 0.0003542
# drugD-1time    9.57920  5.4779183 13.680482 0.0000003
# drugE-1time   15.16555 11.0642683 19.266832 0.0000000
# 4times-2times  3.14981 -0.9514717  7.251092 0.2050382
# drugD-2times   6.13620  2.0349183 10.237482 0.0009611
# drugE-2times  11.72255  7.6212683 15.823832 0.0000000
# drugD-4times   2.98639 -1.1148917  7.087672 0.2512446
# drugE-4times   8.57274  4.4714583 12.674022 0.0000037
# drugE-drugD    5.58635  1.4850683  9.687632 0.0030633
  • Kruskal-Wails 秩和检验
1
2
3
4
5
6

fit = kruskal.test(response ~ trt, data = cholesterol)
fit
# Kruskal-Wallis rank sum test
# 
# data:  response by trt
# Kruskal-Wallis chi-squared = 36.542, df = 4, p-value = 2.238e-07

卡方检验

1、零假设的频率分布

在上面学到方差分析主要是对多组间均值差异比较的方法，样本数据（或者说结局变量）通常为连续型变量；从而探究分组变量的影响。

而卡方检验可以理解为样本数据（或者说结局变量）为分类型变量时，从而探究分组变量的影响。

例如如下数据：探究吸烟是否会影响健康

分组变量(是否吸烟)\结局变量(是否患病) health patient
是 20 10
否 80 15

零假设：吸烟不影响健康。在此前提下，每组（是否吸烟）的发病率应该相同。

由于总发病率为（10+15）/（20+80+10+15） = 20%，而吸烟人数有30人，不吸烟人数有95人。所以理想的列联表频数分布应为

分组变量(是否吸烟)\结局变量(是否患病) health patient
是 30×(1-20%) = 24 30×20% = 6
否 95×(1-20%) = 76 95×20% = 19

2、卡方分布

卡方检验就是比较基于零假设的频数分布于真实频数分布的差距是否具有显著差异，如果有就可以拒绝零假设（在零假设的前提下出现此次观测样本数据的概率很低），认为吸烟会影响健康。

使用皮尔逊残差描述实际频数与理论频数之间的差异

$$ R = \frac{观测频数-预期频数}{\sqrt{预期频数}} \quad R_{1,1} = \frac{20-24}{\sqrt{24}} = 0.82 $$ 所以卡方统计量为所有皮尔逊残差的平方和，计算公式为如下。其中r表示行数，c表示列数。 $$ \chi^2 = \sum_i^r\sum_j^c R^2 $$ 计算得到的卡方统计量符合**自由度为 (r-1)×(c-1)**的卡方分布。如果对于统计量的分布概率值足够小，那么可拒绝零假设，认为分组变量与分类变量有关

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

#
M <- as.table(rbind(c(762, 327, 468), c(484, 239, 477)))
dimnames(M) <- list(gender = c("F", "M"),
                    party = c("Democrat","Independent", "Republican"))
M
#       party
# gender Democrat Independent Republican
#      F      762         327        468
#      M      484         239        477

Xsq <- chisq.test(M)
Xsq
# Pearson's Chi-squared test
# 
# data:  M
# X-squared = 30.07, df = 2, p-value = 2.954e-07

3、Fisher精确检验

（1）上述卡方检验又称Pearson χ2检验。这种检验方式在样本数较少时，结果不太可靠。此时可以考虑使用Fisher精确检验。Fisher精确检验基于超几何分布计算出组合的概率，从而计算P值。

（2）如上例对于总样本数的125人中有25人是病人。现在根据吸烟因素抽出30人，其中有10人是病人。

对于X ~ H(125, 30, 25)的超几何分布，计算出(k=10)的概率– $$ P(X=10) = \frac{C_{25}^{10}×C_{100}^{20}}{C_{120}^{30}} $$

如果P值足够小，可认为不是随机抽样，而是吸烟因素相对富集在病人标签群体。换而言之，吸烟因素影响健康。

最后如果在对有等级关系的分类变量（低、中、高）进行分组比较时，则应选用Wilcoxon秩和检验，而不是卡方检验。

4、R实操

  • 卡方检验
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

# 示例数据：3个党派中，男女人数分布比例
M <- as.table(rbind(c(762, 327, 468), c(484, 239, 477)))
dimnames(M) <- list(gender = c("F", "M"),
                    party = c("Democrat","Independent", "Republican"))
M
#       party
# gender Democrat Independent Republican
#      F      762         327        468
#      M      484         239        477

# 问题：3个党派的男女分布比例是否具有显著差异
Xsq <- chisq.test(M)
Xsq
# Pearson's Chi-squared test
# 
# data:  M
# X-squared = 30.07, df = 2, p-value = 2.954e-07
  • Fisher精确检验
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

# 示例数据：猜测饮料的类别与饮料真实类别的关系
TeaTasting <- matrix(c(3, 1, 1, 3),
                     nrow = 2,
                     dimnames = list(Guess = c("Milk", "Tea"),
                                     Truth = c("Milk", "Tea")))
TeaTasting  
#       Truth
# Guess  Milk Tea
#   Milk    3   1
#   Tea     1   3

# 问题：猜测者是否具有识别饮料类别的能力
fisher.test(TeaTasting, alternative = "greater")
#         Fisher's Exact Test for Count Data
# 
# data:  TeaTasting
# p-value = 0.2429
# alternative hypothesis: true odds ratio is greater than 1
# 95 percent confidence interval:
#  0.3135693       Inf
# sample estimates:
# odds ratio 
#   6.408309
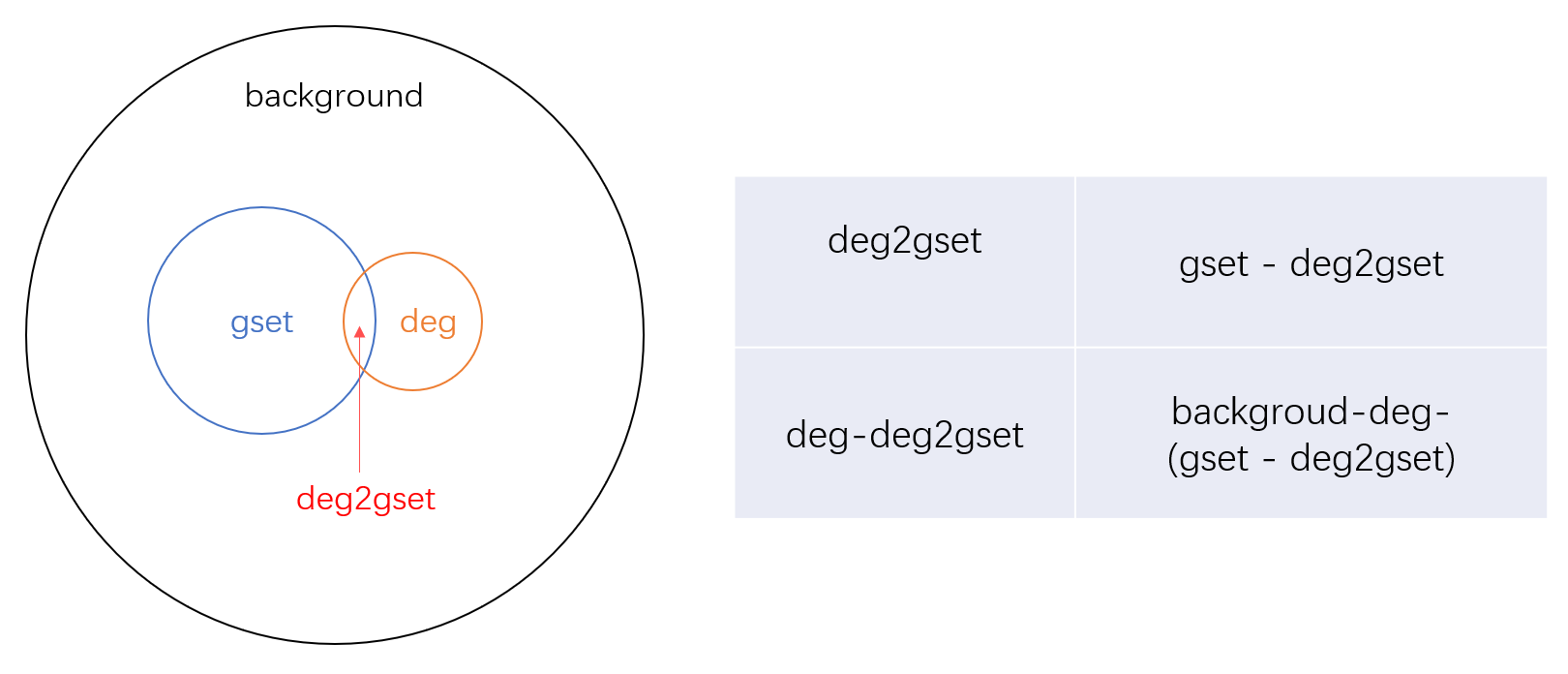
  • 实例：差异基因通路富集分析
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

backgroud = 10000
gset = 500
deg = 100
deg2gset = 50

dat_mt = matrix(c(deg2gset, gset - deg2gset, 
				 deg-deg2gset, backgroud-deg-deg2gset),
				nrow=2, byrow=TRUE)
dat_mt
fisher.test(dat_mt, alternative = "greater")
#         Fisher's Exact Test for Count Data

# data:  dat_mt
# p-value < 2.2e-16
# alternative hypothesis: true odds ratio is greater than 1
# 95 percent confidence interval:
#  14.64419      Inf
# sample estimates:
# odds ratio
#   20.97907

image-20220802103720630