统计学常用样本数据推断总体结果，或者说使用样本统计量推断总体参数。包含如下意义：

（1）对于样本数据，根据问题的不同，会有不同的形式。例如单纯描述一组的数据分布，那么就是原始收集数据；如果描述两组差异，那么差值才是样本数据，而此时目的就是研究总体差值的分布。

（2）理论上来说：总体的参数(均值，方差…)是固定的，但是现实一般做不到；但是从总体抽取的样本数据可以计算样本统计量，但是每一次抽样结果计算的样本统计量存在差异。即抽样误差。

1、中心极限定理

1.1 统计量符合正态分布

假定有一个总体数据，如果从该总体中多次抽样，那么理论上，每次抽样所得的统计量(如均数)与总体参数应该差别不大，大致围绕在总体参数中心，并且呈正态分布（如果是少量样本的话，就是对应自由度的T分布）。

img

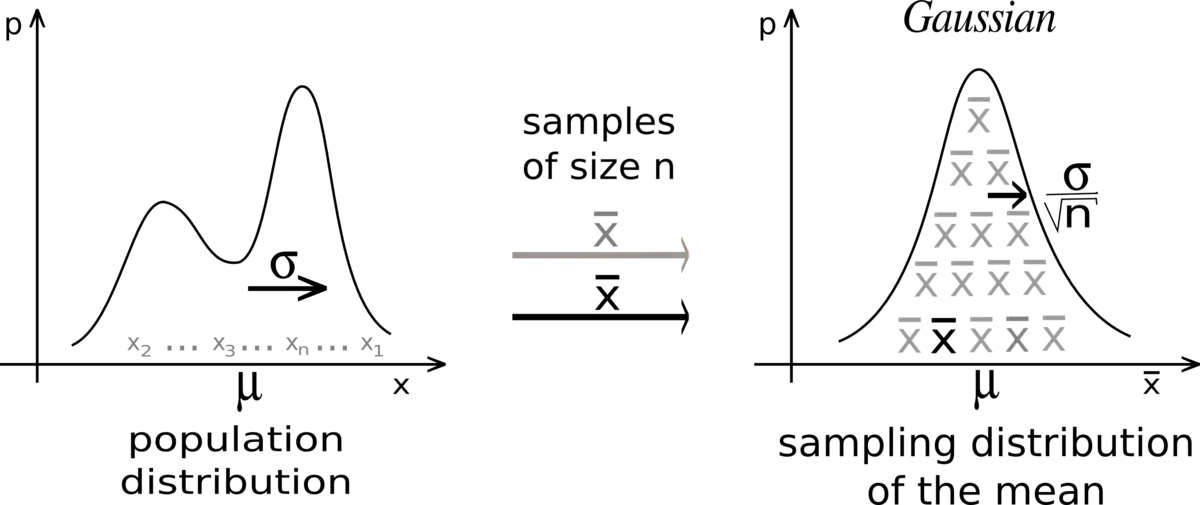
（1）无论原总体数据是什么分布，多次抽样的样本统计量都呈正态分布；

（2）中心极限定理描述的是样本统计量的分布，常见的就是均值。

（3）抽样的样本量越大（大于30），越容易得到一个接近总体参数的统计量（曲线越瘦长）。

1.2 标准误与置信区间

(1) 标准误

由于样本统计量符合正态分布，可以计算出标准误(se, Stand Error)，用以描述表示样本统计量的标准差

  • 标准误越大，表明一次抽样结果计算出的样本统计量难以反映总体水平的真实情况；或者说”准确性“越低。

  • 按照直观理解，计算标准误需要进行多次抽样，然后根据每次抽样的样本统计量计算结果标准误。

但是现实一般都只有一个样本数据，可通过如下公式近似计算：

  • 下述公式中 s表示当前样本数据的标准差，n表示样本数。
    • s越大(样本数据越离散)、n越小(样本数据越少)，则标准误越大；
    • 计算公式由数学推导而得，前提是样本数据符合正态分布。这一点很重要，之后还会提到。

$$ se = \frac{s}{\sqrt{n}} $$

(2) 置信区间

假如使用一组样本数据的统计量(例如均值)去描述总体参数，通常称之为点估计。但是由于抽样误差的存在，样本统计量与总体参数总会存在一定差距，可使用区间估计的方法，描述总体参数的大致范围。

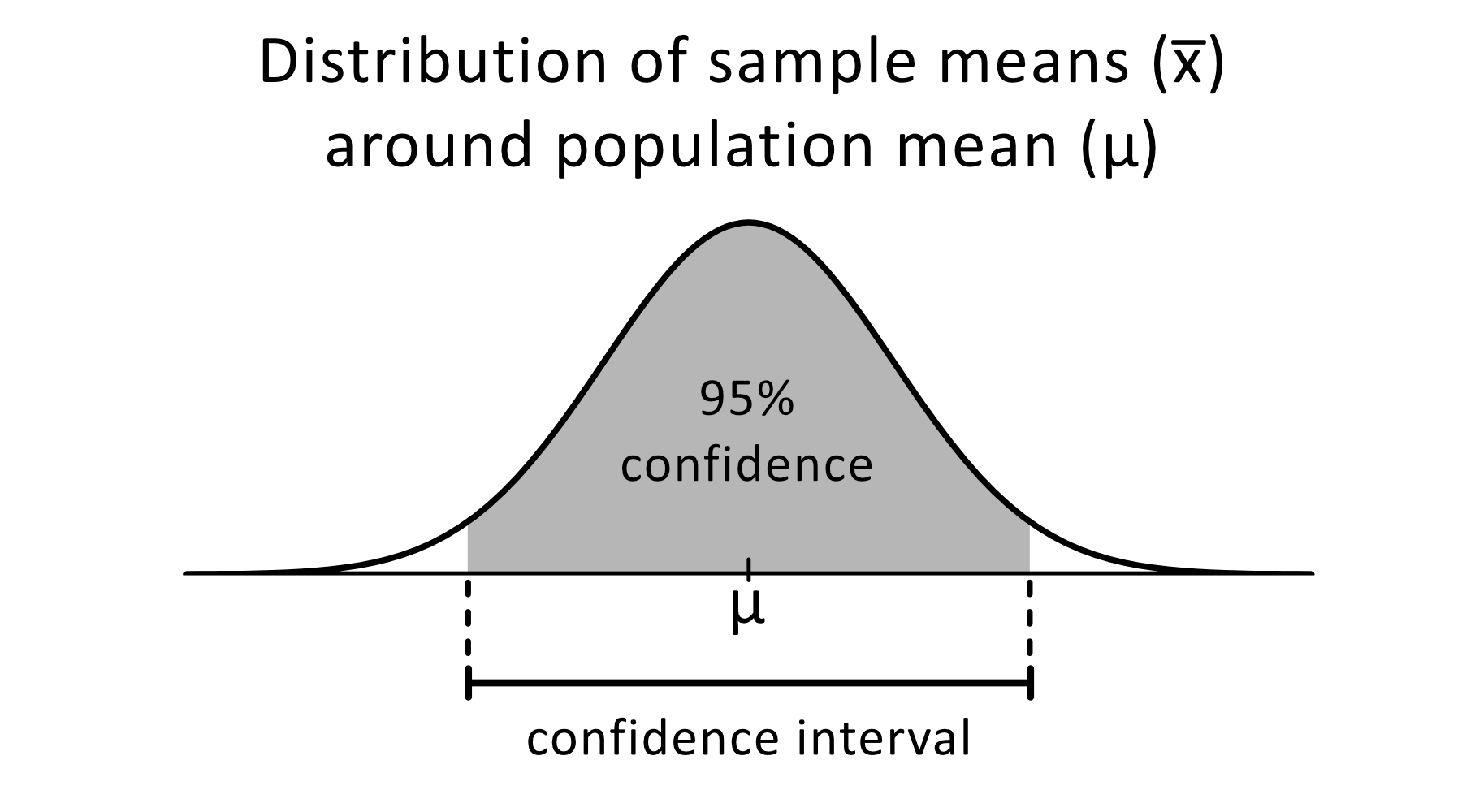
置信区间(confidence interval, CI)：基于标准误的结果，估计某一区间内包含总体参数的可能性。

  • 例如：90%置信区间，表示有90%的信心认为该区间内包含了总体参数。

结合正态分布或者近似正态分布的t分布的曲线下面积规律，可以计算出相应t值/或者z值对应的置信区间。

如下公式表示均数的置信区间： $$ CI \in \overline{x} ,\pm , t × se $$

Confidence Interval Calculator

2、假设检验与T检验

2.1 假设检验

（1）假设检验采用反证法：即设法证明预期结论的完全对立面是不可能发生的。例如判断一个人是好人，就证明他不可能是坏人。

（2）两个假设：

  • 零假设（null hypothesis，H0）：之所以称为零假设，是因为它的假设一般是组间差异为0；两个变量相关系数为0；回归系数为0等
  • 备择假设（alternative hypothesis，H1）：而零假设完全相反的陈述。如组间差异不为0（即有差异）；相关系数不为0（即相关）

（3）零假设是要推翻的。如果零假设是错误的，那么备择假设就一定是正确的。

（4）假设检验通常用于计算得出定性的结论，而不能得出定量的结论。例如两组的均值存在显著差异，但差异幅度是多少是无法获知的。

（5）假设检验的判断基于中心极限定理，即多次抽样的统计量分布符合正态分布（t分布）。下面以T检验为例，解释下假设检验的思路。

2.2 T检验

（1）T检验根据假设检验的思想，常用于检验某一样本统计量是否与总体参数相等。要根据实际问题理解样本统计量与总体参数。

  • 在两独立样本t检验中某样本统计量是两组均值差，总体参数是两总体均值差（常假定为0，即不存在差异）
  • 在回归系数检验中，样本统计量是样本系数，总体参数是总体系数（常假定为，即不存在回归关系）。

以两独立样本t检验为例：先假设两组样本均值不存在差异；然后判断所计算差值的概率是多少。一般认为P<0.05是小概率事件。即两组样本均值不存在差异的概率很小；反之均值存在差异的概率就很大。

（2）应用假设检验的前提是样本数据符合正态分布。当样本数据在比较小(<30)的范围时，则是要符合相应自由度的T分布。

（3）根据具体问题，有三种常见的T检验：[关键是辨析样本数据的定义]

  • 单样本T检验：给定一组样本的数据，判断是否等于某一水平。

    • 例如某班学生成绩是否接近于80分。

      学生 小明 小王 小李 小红 小孙
      成绩 81 90 70 85 76
      样本值 81-80=1 90-80=10 70-80=-10 85-80=5 76-80=-4

    • 如上表，该问题转换为 [1, 10, -10, 5, -4]这组数据的统计量(1+10-10+5-4)/5=0.4出现在均值为0，标准差为se（参考极限中心定理的标准误计算公式，取决于样本标准差与样本数）的零假设统计量的t分布的可能性是多少？

  • 配对T检验：给定一一对应的两组数据，判断两组间水平是否存在差异。

    • 例如取10个癌症患者的各自癌旁与癌组织测序，分析某一基因的表达是否存在差异。

      病人 01 02 03 04 05
      癌组织 10 12 24 15 19
      癌旁组织 8 9 12 10 11
      样本值 10-8=2 12-9=3 24-12=12 15-10=5 19-11=8

    • 如上表，该问题转换为 [2,3,12,5,8]这组数据的统计量(2+3+12+5+8)/5=6出现在均值为0，标准差为se（参考极限中心定理的标准误计算公式，取决于样本标准差与样本数）的零假设统计量的t分布的可能性是多少？

    • 所以配对T检验本质上还是单样本T检验。

  • 独立样本T检验：不同来源的两组数据，判断两组水平是否存在差异。

    • 例如取10个癌症患者的血液，与5个健康人的血液样品测序，分析某一基因的表达是否存在差异。

      编号 P01 P02 P03 P04 P05 H01 H02 H03
      组别 患者 患者 患者 患者 患者 健康 健康 健康
      结果 12 15 11 14 14 10 11 9
      组均值 13.2 13.2 13.2 13.2 13.2 10 10 10

    • 如上表，该问题转换为样本统计量13.2-10=3.2出现在均值为0，标注差为se（参考极限中心定理，取决于样本标准差与样本数）的零假设统计量的t分布的可能性是多少？

    • 对于独立样本T检验中标准误的计算，根据两组数据的方差是否相同有两种不同处理方式。但仍与各组的方差与样本数有关。

上面三种方法最终都会计算出t值，继而求出在对应自由度的零假设T分布中出现该t值（甚至）更大的概率，即P值。

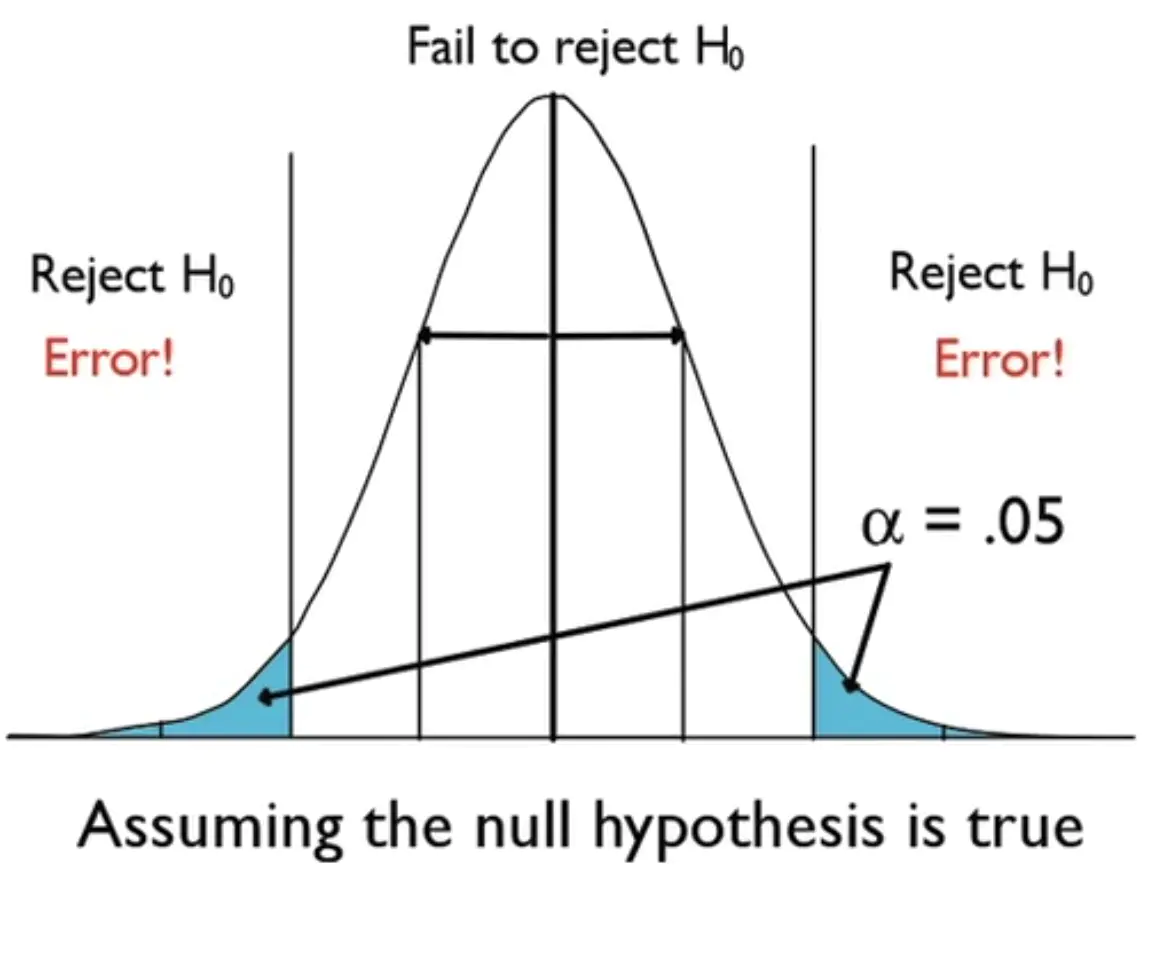
  • 对于双侧检验（零假设 H0: Udiff=0）:计算两端的概率；对于单侧检验（零假设H0：0）: Udiff>0 计算右侧的概率；Udiff<0 计算左侧的概率
  • P值可以理解为：在零假设成立的前提下，出现如此t统计量的概率是多少。P值越小，表明越不可能出现，即零假设越不可能成立；进而支持其对立面的备择假设。

$$ t = \frac{样本统计量-总体参数}{样本统计量的标准差(标准误)} $$

img

假如样本数据不符合正态分布，那么理论上就不可以使用T检验。可以选择非参数检验的Wilcoxon秩和检验，将样本数据转换为秩（排名）进行假设检验分析。

2.3 两类错误

假如把看病问题视为假设检验，零假设为健康，备择假设为患病。

当医生碰到一个经常锻炼的运动员时较容易正确判断是健康人，碰到一个咳嗽不停的人时较容易争取判断是病人；但是遇到一个处于这两者中间状态的人，判断时需要谨慎：以免娇弱的人误诊为病人（假阳性）；有前兆的病人漏诊为健康人（假阴性）。

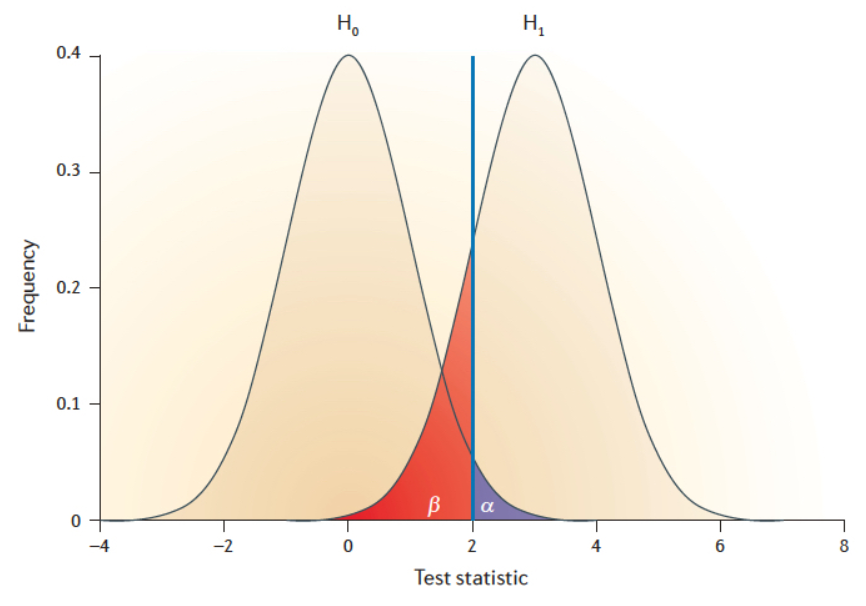
假设检验中的两类错误- 那抹阳光1994 - 博客园

根据假设检验的P值结果得出的结论，会不可避免出现下面两种错误的可能：

  • 假阳性(FP, False Positive)又称为第一类错误，错误地认为H1是正确的，用α表示；如上图蓝色区域(娇弱的人)；

  • 假阴性(FN, False Negative)又称为第二类错误，错误地认为H1是不存在的，用β表示；如上图红色区域(有前兆的病人)

这两类错误的出现是此消彼长的关系：

  • 当P值很小，才判定H0假设为不可能事件时–α降低；β增高

    • 宁可漏诊，不能错诊。

  • 一般来说更加重视假阳性的结果，即将P值的阈值定位非常低的水平。

3、T检验基于R

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

# 两种安眠药(与控制组相比所增加的睡眠时间)对10名患者的影响。 
data(sleep)
table(sleep$group)
# 1  2 
# 10 10
head(sleep)
#   extra group ID
# 1   0.7     1  1
# 2  -1.6     1  2
# 3  -0.2     1  3
# 4  -1.2     1  4
# 5  -0.1     1  5
# 6   3.4     1  6

3.1 单样本T检验

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

t.test(extra ~ 1, data = sleep)
# One Sample t-test
# 
# data:  extra
# t = 3.413, df = 19, p-value = 0.002918
# alternative hypothesis: true mean is not equal to 0
# 95 percent confidence interval:
#   0.5955845 2.4844155
# sample estimates:
#   mean of x 
# 1.54 

t.test(extra ~ 1, data = sleep)$p.value
t.test(sleep$extra ~ 1)

3.2 独立样本T检验

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

t.test(extra ~ group, data = sleep)
# t.test(extra ~ group, data = sleep)
# Welch Two Sample t-test
# 
# data:  extra by group
# t = -1.8608, df = 17.776, p-value = 0.07939
# alternative hypothesis: true difference in means between group 1 and group 2 is not equal to 0
# 95 percent confidence interval:
#   -3.3654832  0.2054832
# sample estimates:
#   mean in group 1 mean in group 2 
# 0.75            2.33 

t.test(extra ~ group, data = sleep)$p.value
t.test(sleep$extra[sleep$group==1],
       y = sleep$extra[sleep$group==2])

3.3 配对样本T检验

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

t.test(extra ~ group, data = sleep, paired = TRUE)
# Paired t-test
# 
# data:  extra by group
# t = -4.0621, df = 9, p-value = 0.002833
# alternative hypothesis: true difference in means is not equal to 0
# 95 percent confidence interval:
#   -2.4598858 -0.7001142
# sample estimates:
#   mean of the differences 
# -1.58 

t.test(extra ~ group, data = sleep, paired = TRUE)$p.value
t.test(sleep$extra[sleep$group==1],
       y = sleep$extra[sleep$group==2], paired = TRUE)

3.4 wilcox.test秩和检验

将上述的t.test()替换为wilcox.test()，即可执行对应方式的秩和检验。

Performs one- and two-sample Wilcoxon tests on vectors of data; the latter is also known as ‘Mann-Whitney’ test.

1
2
3
4
5
6
7
8

##(1)单样本
wilcox.test(extra ~ 1, data = sleep)

##(2)两独立样本
wilcox.test(extra ~ group, data = sleep)

##(3)配对样本
wilcox.test(extra ~ group, data = sleep, paired = TRUE)