统计的对象是数据，其中会涉及到不同类型的数据；统计的目的是描述，描述一组数据的分布特征、两组至多组数据之间的关系。

1、数据分类

根据数据特点，可以分为2大类：

1.1 数值型数据

  • 连续型数据：可在一个数值范围内任意取值的数据，特点之一就是允许包含小数。例如身高值。

  • 离散型数据：只能取整数的数据，多见于计算次数的数据。例如每分钟跳绳次数。

    计数数据是离散型数据，反之不是。

1.2 分类型数据

  • 二分类数据：只有两个类别。例如生死。

  • 无序多分类：多种类别，无逻辑上的顺序关系。例如职业分布。

  • 有序多分类：多种类别，有逻辑上的顺序关系。例如考试等级。

    （1）分类资料的有序与无序有一定的主观性。可以把有序资料视为无序资料，反之亦然。

    （2）另外可通过对数值型数据划分阈值，转换为分类数据。

2、统计描述

给定一组连续型数据，可以从下面三个角度进行描述。

2.1 数据位置估计

位置估计指该组数据的”代表值“，最常见的是均值；而中位数更稳健，适用于含有离群点的数据。

（1）均值

一般均值：累加的和除以个数 $$ \overline{X} = \frac{\sum_{i=1}^{n}x_i}{n} $$ 截尾均值：去掉若干(p)个最小值与若干(p)个最大值的均值 $$ \overline{X} = \frac{\sum_{i=p+1}^{n-p}x_i}{n-2p} $$ 加权均值：数值乘以权重的求和除以权重和 $$ \overline{X_w} = \frac{\sum_{i=1}^{n}x_iw_i}{\sum{_{i=1}^{n}}{w_i}} $$

（2）中位数

中位数：将数据进行排序，处于中间位置的数据。是对位置的健壮估计，不收离群值影（极端值）响。

加权中位数：将原始数据进行排序，该值上半部分的权重和等于该值下半部分的权重和。

2.2 数据变异估计

变异估计去评价一组数据是紧凑的，还是分散的。

（1）方差

  • 偏差：均值与每一个实际值的差异。也称为误差、残差。

  • 平均绝对偏差：差值的绝对值的平均数。 $$ \frac{\sum_{i=1}^{n}|x_i-\overline{x}|}{n} $$

  • 方差：偏差平方的平均数。

$$ s^2 = \frac{\sum_{i=1}^{n}(x_i-\overline{x})^2}{n-1} $$

在大样本下（即n特别大），除以（n-1）还是除以（n）区别不大。如果在小样本时，除以（n）会低估观测值的变异度，称之为有偏估计。这里涉及到了自由度的影响，之后还会提到。

  • 标准差(standard deviation, sd)：方差的平方根。

上述指标均为基于均值的统计，容易受到极端离群值的影响。变异性的一种健壮估计是中位数绝对偏差，成为MAD：

$$ MAD = 中位数(|x_1-m|, |x_2-m|, …,|x_N-m|) $$

（2）分位数

  • 百分位数：第P个百分位数指的是 > P%的值，而 < (1-P)%的值。

  • Q1表示第25百分位数，Q2表示第50百分位数（即中位数），Q3表示第75百分位数。

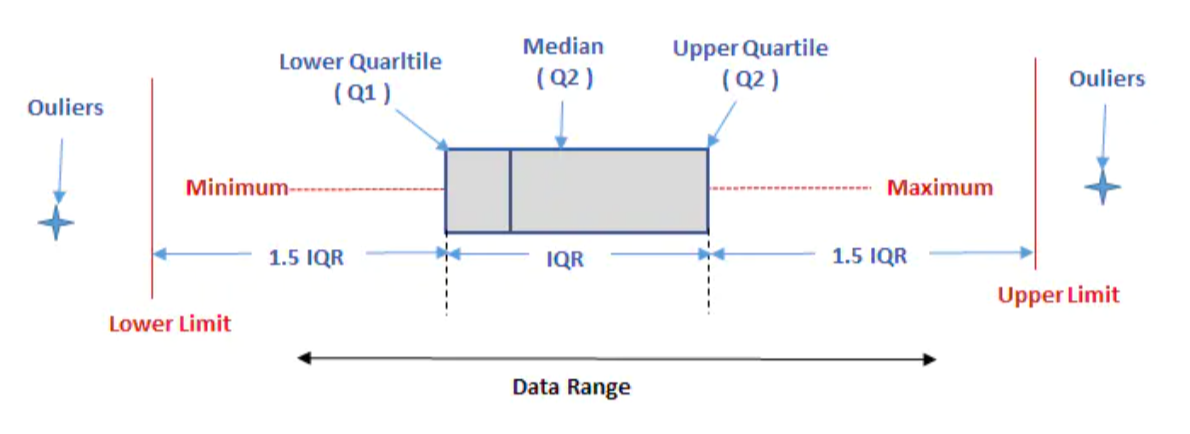
  • 四分位距（IQR）= Q3-Q1，可用于描述一组数据的变异性

  • 箱线图就是依据百分位数绘制的。

image-20220422125301381 

1
2
3
4
5
6
7

x = 1:100
quantile(x)
# 0%    25%    50%    75%   100% 
# 1.00  25.75  50.50  75.25 100.00 
quantile(x, probs = c(0.3, 0.6,0.9))
# 30%  60%  90% 
# 30.7 60.4 90.1

2.3 数据分布估计

  • 直方图：将数据分布范围分为若干个连续的bin，每个bin的长度相同。然后进一步统计处于每个bin中的数量。纵坐标表示为频数。
  • 密度图：可以理解为直方图的平滑表示，即bin的宽度无限小化。纵坐标表示为概率，曲线下面积等于1；所以概率密度图。

img

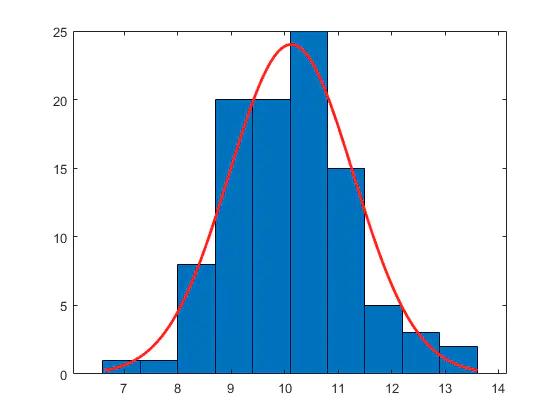
  • 概率密度函数：用一个函数方程去描述/预测某个观测值出现的概率，绘制概率密度曲线。不同类型的概率密度函数具有不同的分布特征，适用于不同类型的数据。比如正态分布，二项分布……，其本质上就是描述了数据的分布特征。

3、常见分布

3.1 正态分布

（1）正态分布

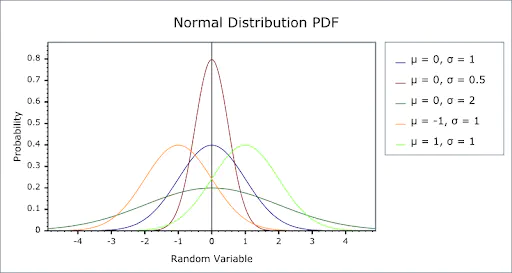
  • 数据围绕均值波动，曲线呈钟形。具体的形状取决于数据的两个特征值：（1）均值；（2）方差 $$ X \sim N(\mu, \sigma^2) $$

img

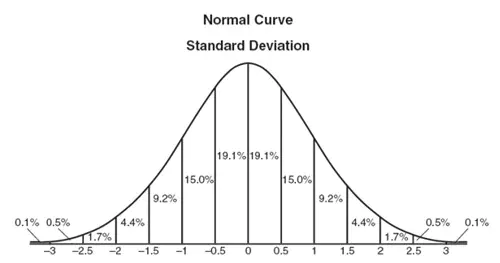
  • 正态分布的数据分布很有规律性：以均值为中心，±1σ面积为68.2%；±2σ面积为95.4%；±3σ面积为99.7%

  • zscore标准化：数据与均值的差值，再除以标准差的比。它反映了某个值偏离均数的标准差倍数。 $$ Z = \frac{X-\mu}{\sigma} $$

    由Z值组成的数据分布称为均值为0，方差为1的标准正态分布。Z值可直观表示某个观测值在一组数据中所处的位置，例如Z=0，表示处于中间位置；Z=1，表示约处于第84百分位数的位置。

img 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

rnorm(5)
#[1] -1.1093736  0.6631883  0.1295332 -1.5635006  0.5994136
rnorm(5, mean = 10, sd = 10)
#[1] 13.5595849  0.2666945 12.9323366  2.0843432 19.4443122

dnorm(1)           #密度概率
# [1] 0.2419707
pnorm(1)           #累积分布
# [1] 0.8413447

qnorm(0.5)         #分位数
# [1] 0


##下同，每种分布都有上述4类函数

（2）T分布

  • t分布可以理解为小样本的标准正态分布，相对于标准正态分布曲线更加扁平；
  • t分布是一簇分布，随着样本量/自由度的增加，越接近标准正态分布(n>30)；
  • 在自由度=5时，右侧2.5%面积对应t值为2.57；自由度=30时，右侧2.5%面积对应t值为2.04。（标准正态分布的右侧2.5%面积为1.96）

img

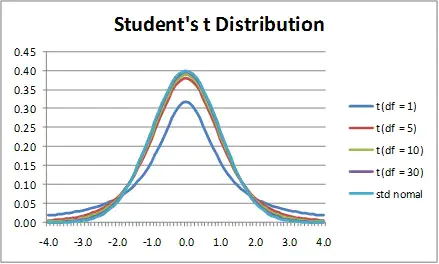
常用于两个均数是否相等，系数是否为0等

1
2

rt(5, df=5)
# [1] -2.95051051 -0.54738086 -1.60480176  1.13751489  0.08116877

（3）χ2卡方分布

  • 卡方分布衍生自标准正态分布。

  • 假设一组观测值符合标准正态分布，那么其所有观测值的平方符合自由度为1的卡方分布。

$$ X = Z_1^2 \quad\quad X \backsim \chi^2(1) $$

Z1 = （ 0.16, -0.07, -1.07, -0.44, 0.90）

S1 = Z1平方 = （0.0256, 0.0049, 1.1449, 0.1936, 0.8100）

即X = S1符合自由度为1的卡方分布。

  • 对于多组(n)均符合标准正态分布的观测值，那么其各组平方值跨组相加的结果，符合自由度为n的卡方分布。

$$ X = Z_1^2 + Z_2^2 + …Z_n^2 = \sum_{i=1}^{n}Z_i^2 \quad\quad X \backsim \chi^2(n) $$

Z1 = （ 0.16, -0.07, -1.07, -0.44, 0.90）; Z2 = (-1.40, 0.00, 0.98, -0.92, -1.12)

S1 = Z1平方 = （0.0256, 0.0049, 1.1449, 0.1936, 0.8100）

S2 = Z2平方 = （1.9600, 0.0000, 0.9604, 0.8464, 1.2544）

S1 + S2 = （1.9856 0.0049 2.1053 1.0400 2.0644）

即X = S1 + S2 符合自由度为2的卡方分布。

  • 卡方分布曲线特征只取决于自由度（因为是由标准正态分布转换而来）

img

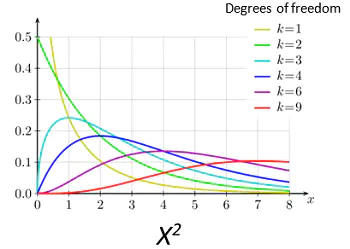
卡方分布多用于描述分类资料的实际频数与理论频数之间的抽样误差。

1
2
3

# shape= 交代自由度
rgamma(5, shape = 3)
# [1] 3.054343 2.324643 2.898174 2.223752 3.088181

（4）F分布

  • 若随机变量X符合自由度为m的卡方分布，随机变量Y符合自由度为n的卡方分布。则(X/Y) 符合自由度为m,n的F分布。
  • 如上，F分布有两个参数分别为分子自由度与分母自由度。

$$ X \backsim \chi_m^2, , Y \backsim \chi_n^2 \quad\quad F = \frac{X/m}{Y/n} $$

img

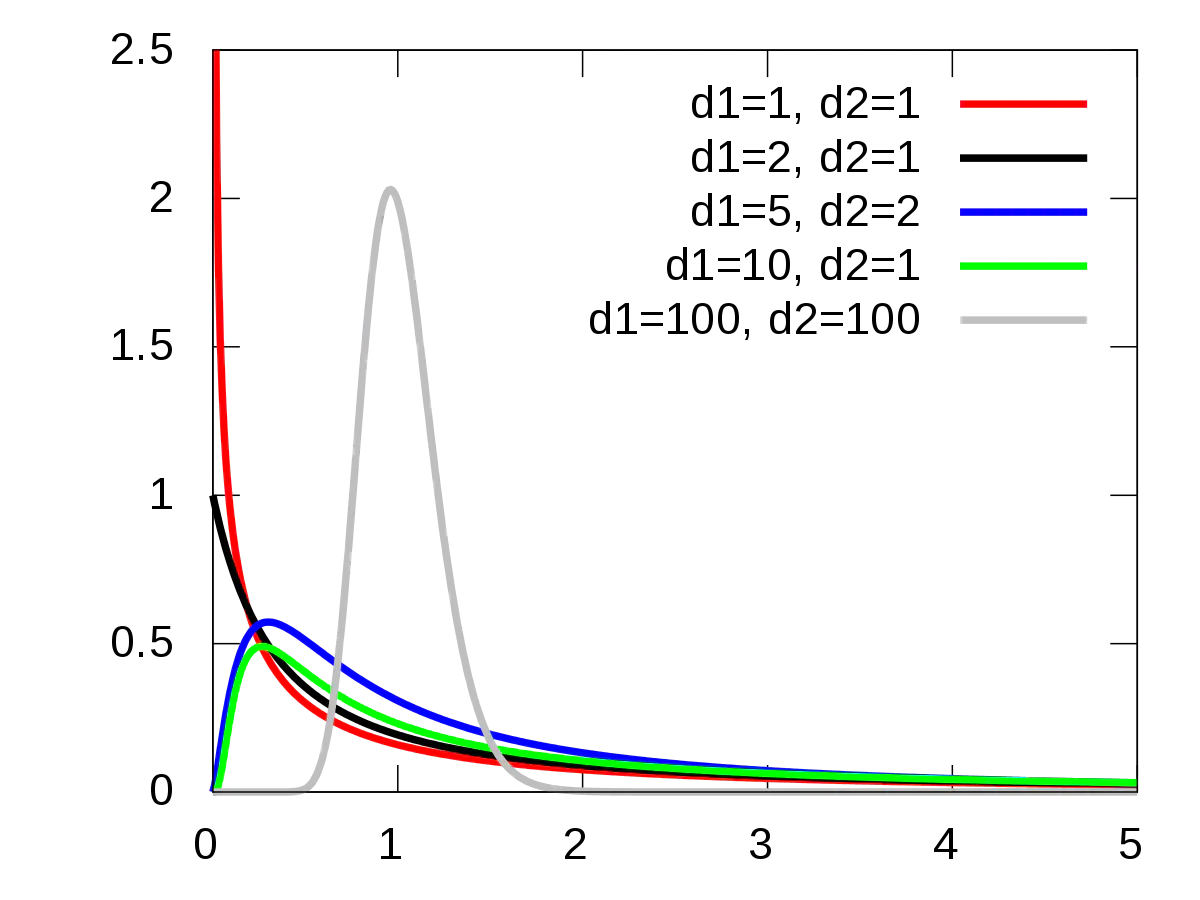
F分布多用于方差比的相关分析，例如方差分析是组间方差与组内方差之比。

1
2

rf(5, df1 = 5, df2 = 1)
#[1] 1.554777e+03 5.389789e-02 3.793949e+01 1.923800e+00 3.065202e+00

3.2 二项分布

（1）二项分布

  • 给定实验次数n，以及每次实验次数成功的概率p，那么成功次数x(0≤x≤n)的概率符合参数为（n，p）的二项分布。

$$ X \backsim b(n,p) $$

  • 关于二项分布的期望值与方差的计算公式为 $$ \mu = np,; \quad\quad \sigma^2 = n\cdot p\cdot (1-p) $$

    关于方差的计算公式直观上难以理解，是由二项分布函数推导得到的。

  • 例如抛硬币实验，定义抛出正面为实验成功，已知正面概率为0.7。假设全班同学每人抛了20次，那么计算出有多少比例同学会抛出了10次以上的正面结果。

Probability mass function for the binomial distribution

  • 二项分布是离散分布，横坐标表示每次实验发生次数。在规定一个N值很大的情景，即很多次实验的前提下，二项分布可以近似表示为均值为u的正态分布（连续分布）。当n越大（至少20）且p不接近0或1时近似效果更好。

伯努利试验（Bernoulli trial，或译为白努利试验）是只有两种可能结果（“成功”或“失败”）的单次随机试验。

1
2

rbinom(10, size=5, prob=0.3)
#[1] 1 1 1 2 2 0 1 2 0 1

（2）泊松分布

  • 泊松分布：用于估计每时间单位或者空间单位条件下，事件所发生的的平均次数。分布特征仅取决于参数：平均次数λ
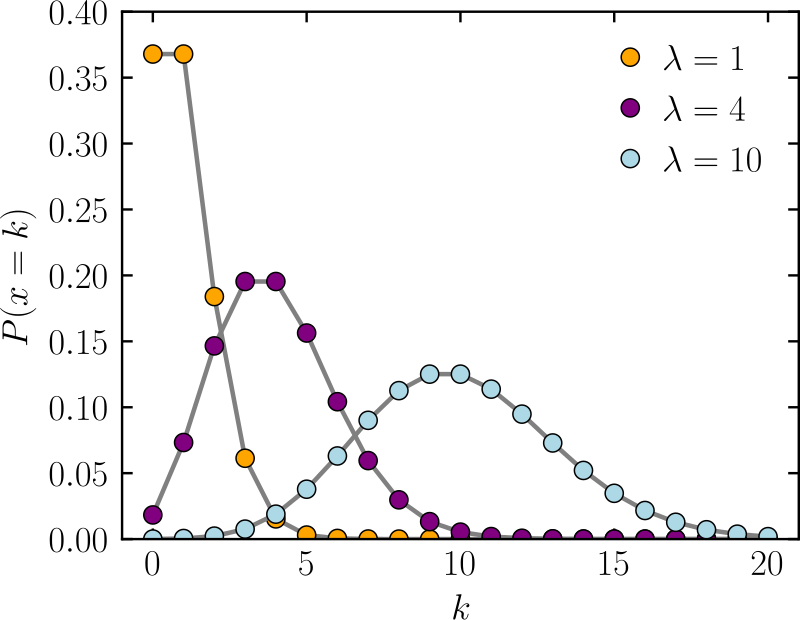
upload.wikimedia.org/wikipedia/commons/thumb/1/...

  • 可以认为是二项分布的特例。即N非常大，P非常小。例如每次中彩票的人数；每年患流感的人数；在每个样本RNAseq文库中比对到GeneA的count数，实验背景总数很多，但是事件发生的概率很小。当n≧20,p≦0.05时。

  • 根据二项分布中期望与方差的计算公式，可以推导出在泊松分布中 期望值（即λ）=方差。 $$ \lambda = np \approx n\cdot p\cdot (1-p) = \sigma^2 $$

1
2

rpois(10, lambda=5)
# [1]  9  4  5  3  7  7  6  6  4 10

负二项分布：对于一次伯努利试验中，事件成功的概率为p。反复进行该伯努利试验，直到观察到第r次成功发生。此时试验失败次数X的分布即为负二项分布

（4） 超几何分布

假设在N个物体中，有一组特殊标签的K个物体。当对所有物体不放回地抽出n个物体时，其中k个属于该标签的概率。

  • 示例-1：N为所有产品数，K为其中不合格样本数。从中抽取n个产品中，有k个产品为不合格概率；
  • 示例-2：N为所有基因数，K为通路A的基因数。分析得到n个差异基因，有k个基因属于该通路的概率。

$$ X \sim H(n, K, N) $$

Hypergeometric PDF plot 

1
2
3
4
5

# n为合格产品数
# m为不合格产品数
# k为抽检的数目
rhyper(5, m=10, n=50, k=5)
# [1] 0 1 0 2 0